10.3 Наиболее употребительные распределения. Замена переменных

0. Вырожденноераспределение.X=C=const

0. Распределение Бернулли. Этому распределению отвечает следующая схема испытаний: имеется опыт с двумя исходами (1 — «успех», 0 — «неудача»), заданы вероятностиP(X= 1) =p,P(X= 0) = 1 −p=q.

x	0	1
p	p	q

Функция распределения имеет вид

0. Биномиальное распределение. Производитсяnнезависимых испытаний, а исходы кодируются двоичной последовательностьюωдлиныn(0 отвечает неудаче, 1 — успеху). За случайную величину беретсяX(ω) =m— число успехов. Из §9 знаем, что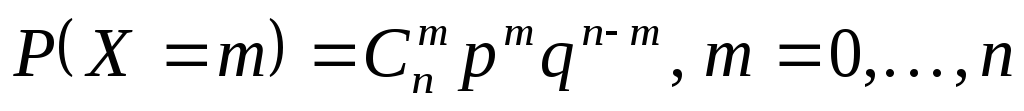. Таблица распределения имеет вид (∑ p_i = 1):

x	0	1		n
p	p0	p1		pn

Функция распределения

0. Распределение Пуассона

Случайная величина принимает значения 0, 1, 2, …, n, …, причем



λ	0	1		n
p	p0	p1		pn

0. Равномерное распределениена конечной совокупности

x	x1	x2		xn
p	1/n	1/n		1/n

0. Равномерное распределениена интервале [a,b]

Из интервала выбирается точкаω;X(ω) =ω.

Плотность распределения вероятности равна

.

Функция распределения

.

Теорема(преобразование Смирнова). ПустьХ — случайная величина с непрерывной функцией распределенияF, тогдаF(x) =Y — новая случайная величина, имеющая равномерное распределение на [0,1], т.е.

.

Доказательство. ЕслиFмонотонно возрастает, существует обратная функцияF⁻¹, и тогда

.

0. Показательноераспределение

.

Функция распределения

.

0. Симметричное показательное распределение

0. Нормальное распределение. Говорят, что случайная величинаXимеет стандартное нормальное распределение, если плотность распределения равна

,

и нормальное распределение с параметрами aиσ, если плотность ее распределения

.

(у стандартного нормального распределения a= 0,σ= 1).

График нормального распределения:

0. Распределение Коши — пример распределения с плохими свойствами:

.

Примеры

1. Маяк, расположенный в 1 км от прямоугольного берега, посылает луч под углом α, имеющим равномерное распределение в интервале [−π/2,π/2]. Найти плотность и функцию распределения координаты лучаx.

.

.

2. Случайная величина Xимеет равномерное распределение на [a,b];F(0) = 1/4,F(1) = 1/2. Найти параметры распределения (a иb).

Как известно,

.

Подставим вместо x — 0 и 1, и решим получившуюся систему уравнений

.

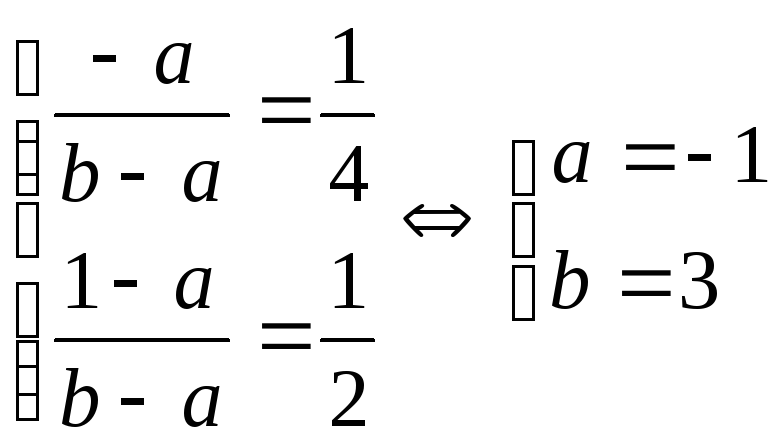График функции распределения (качественно):

3. Случайная величина Xимеет показательное распределение с параметромα. Найти плотность распределения величиныY=exp x.

Решение.

,.

4. Случайная величина Xнормально распределена с параметрамиaиσ, т.е.

.

Найти вероятность того, что X(1,3).

Решение.

,

где Φ — функция Лапласа:

.

Обобщим результат примера 4 — докажем теорему о плотности распределения преобразованного вектора. Пусть дана случайная величинаXс плотностью распределенияp_X(x),Y=φ(X). Требуется найти плотность распределенияp_Y(y).

Будем считать φ(X) монотонна и дифференцируема (вообще говоря, монотонность требуется для взаимно-однозначного отображенияX↔Y).

Предположим, φ(X) монотонно возрастает (для монотонного убывания доказательство аналогично). В таком случае.

По правилу дифференцирования обратной функции можно также записать

.

Доказательство.

.

Продифференцируем это выражение по y:

.

Пусть теперь φ(X) монотонно убывает. Тогда

.

Продифференцировав, получим знак «−» перед выражением для p_Y. Однакопри этом также будет отрицательной величиной. Отсюдавывод: в общем случае формула имеет вид. Теорема доказана.

Рассмотрим важный случайприменения теоремы. Пустьφ(X) — линейная функция, т.е.φ(X) =aX+b. Тогда. Отсюда,

.

В частности, если X~N(0, 1)⁹,Y=aX+b, то

Вывод: при линейном преобразовании получили величину с нормальным распределениемN(b,a²). И наоборот: если дана величинаY~N(a,σ²), тоимеет стандартное нормальное распределение. С учетом этих результатов пример 4) решается более просто: нам дано 1 ≤X≤ 3, гдеX~N(a,σ²). Возьмем, тогда

.

Проинтегрировав p_Y(y) в пределах от (1−a)/σдо (3−a)/σ, получим то же самое.

5. Пусть X~U(0, 1),Y= −alnX+b. Найтиp_Y(y).

Решение. Применим теорему:

.

Отсюда

,y>b.

При b= 0 получаем показательное распределение.

Замечание. Вообще говоря, теорема не всегда применима. Действительно, пустьX~N(0, 1), аY=X ². Легко видеть, чтоX ²немонотонна, но в данном конкретном случае плотность распределения найти можно:

.