Тема2. Елементи векторної алгебри. Вектори в просторі r3.

План

1. Система координат в просторі (побудова точки за її координатами). Відстань між двома точками.

2. Означення вектора. Модуль вектора. Координати вектора та їх знаходження.

3. Розклад вектора за ортами.

4. Лінійні дії з векторами заданими геометрично і аналітично (додавання, віднімання, множення вектора на число).

5. Означення скалярного добутку векторів, його обчислення і застосування.

1 . z

К

y

j

x 0

i

Побудувавши точки А (-3;2;1), В (0;-2;1), С (0;3;0),

z

А (-3;2;1)  R₃

В (0;-2;1)  YZ

С (0;3;0)  OY

0

c y

x

2. Вектором називають величину, яка характеризується не тільки своїм числовим значенням (довжиною), але й напрямом, тобто геометрично – це напрямлений відрізок.

Вектори позначають а, в, с або АВ, СD.

Довжину (модуль) вектора позначають |а|, |АВ|

Нульовим вектором називають вектор початок і кінець якого співпадають.

Рівними називають вектори, які мають однакові довжини та напрямки.

Колінеарними називають вектори, які розташовані на одній прямій або паралельних прямих.

Протилежними називають колінеарні протилежно спрямовані вектори однакової довжини.

Координатами вектора називають проекції вектора на координатні осі.

а_х=|а| cos , а_y=|а| cos , а_z=|а| cos , де cos , cos , cos , називають напрямними косинусами вектора а.

Координати вектора М₁ М₂ дорівнюють різниці відповідних координат кінця та початку вектора.

Проекцією вектора АВ на вісь називається довжина вектора АВ_, яка взята із знаком “+”, якщо напрям АВ співпадає з напрямом осі та із знаком “-“, якщо напрями протилежні

а_х=пр_аха; а_y=пр_аyа; а_z=пр_аzа;

Модуль вектора АВ обчислюється за формулою:

d_АВ=(х₁-х₂)²+(y₁-y₂)²+(z₁-z₂)²

Напрям вектора у просторі задають напрямні косинуси.

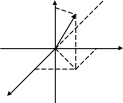Z A

а_z

x а_y y a = OA_z + OA_xy = OA_x + OA_y + OA_z

A_x

а_х A_xy a = a_xi + a_yg + a_zk – це розклад вектора за ротами.

x

Таким чином аналітично вектор можна задати: а(а_x;а_y;а_z;) або а=a_xi+a_yg+a_zk.

3. Ортом вектора а називають вектор а, довжина якого дорівнює 1, а напрям співпадає з а, тобто а=|а|*а₀.

і (1;0;0) орти або одиничний базис простору R₃.

g(0;1;0)

k(0;0;1)

4. Сумою двох векторів а та b називають вектор с, який сполучає початок вектора а з кінцем вектора b при умові, що початок вектора b вміщено в кінець вектора а.

Різницею двох векторів а та b будують як суму вектора а та вектора (-b).

Добутком вектора а на число к називають вектор b=к*а, колінеарний з вектором а, що має довжину в к раз більшу, ніж а та напрям такий самий як а, якщо к>0, і протилежний до а, якщо к<0.

Щоб помножити вектор а на число к, треба всі координати вектора помножити на число к, тобто

ка=(ка_1, ка_2, ,ка_n, ).

Правило знаходження алгебраїчної суми векторів. Координати алгебраїчної скінченної кількості векторів дорівнюють такій же алгебраїчній сумі відповідних координат цих векторів..

а=(а₁, а₂, , а_n), b=(b₁, b₂, , b_n), с=(с₁, с₂, , с_n),

їх алгебраїчна сума а-b+с знаходиться за формулою:

а-b+с=(а₁-b₁+с₁, а₂-b₂+с₂, , а_n-b_n+с_n);

5. Скалярним добутком векторів а та b називають число, яке дорівнює добутку модулів цих векторів на косинус кута  між ними.

Скалярний добуток векторів а та b позначають а*b або (а, b).

Отже згідно з означенням а*b=|а|*|b|*cos.

Кутом між двома векторами (або між вектором та віссю) називають найменший кут між її напрямами при умові, що вектори зведено до спільного початку.

Знаходження скалярного добутку векторів а та b. Згідно з правилом множення матриць одержуємо

b₁

a*b(а₁, а₂ , а₃)* b₂ =a₁*b₁+a₂*b₊a₃*b₃,

b₃

тобто скалярний добуток двох векторів дорівнює сумі їх однойменних координат.

Якщо відомо координати векторів, то скалярний добуток знаходять за формулою:

a*b=a_x*b_x+a_y*b_y+...+a_z*b_z,

i*g=0 a*a=|a|*|a|*cos 0⁰=|a|²,

i*i=1 a²=|a|²,

Умова перпендикулярності векторів:

a*b=0, бо cos 90⁰=0

Умова колінеарності векторів

a_x/b_x=a_y/b_y=a_z/b_z;

Приклад 1.

Дано: вектор а=3і-2у+к, b=-g+2r, c=2і-3d,

Знайти: 1) модуль вектора а, b, c; 2) напрямні косинуси для вектора а; 3) 2а-3b; b+с; 4) а скалярно помножити на b; 5) (2а-3b) (3b+c); 6) косинус  між а і b.

1) |a|=3²+(-2)²+1²=9+4+1=14

|b|=0²+(-1)²+4²=5

|c|=2²+(-3)²+0²=13

2) Напрямні косинуси для вектора а:

cos=а_х / |а|=3/140,8, cos=а_у / |а|=-2/14-0,5,

cos=а_z / |а|=1/140,3,

3) 2а-3b=2(3;-2;1)-3(0;-1;2)=(6;-4;2)-(0;-3;6)=(6-0;-4+3;2-6)=(6;-1;-4)

b+с=(0;-1;2)+(2;-3;0)=(2;-4;2)

4) а(3;-2;1), b(0;-1;2)

а*b=(3*0+(-2)*(-1)+1*2)=(0+2+2)=4

(2а-3b)*(3b+c)=(6;-1;-4)*(0;-3;6)+(2;-3;0)=(6;-1;-4)*(2+0;-4+(-3);6+0)=(6;-1;-4)*(2;-6;6)=(6*2+(-1)*(-6)+(-4)*6)=(12+6-24)=-6

5) Знайдемо cos  між а і b:

а*b=|а|*|b|cos , звідси

cos =а*b / |a|*|b|=(3;-2;1)*(0;-1;2) / 14*54 / 700.5

cos =0.5