10. Теорема Кронекера – Капеллі.

Якщо для системи (1.1):

1. r 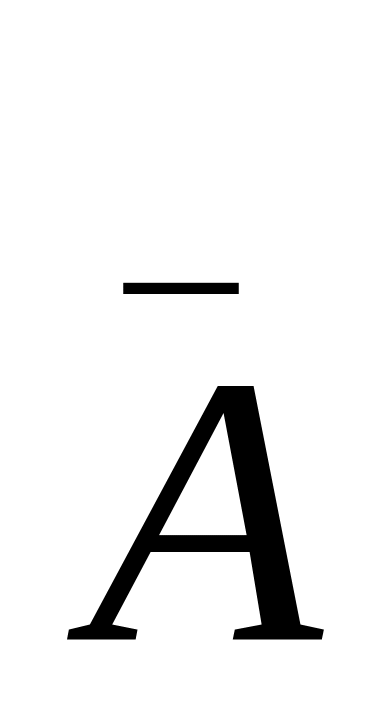= r_A = r = m, то система має єдиний розв’язок.

2. r = r_A = r ≠ m, то система має безліч розв’язків, r – невідомих називають базисними, m–r – вільними.

3. r ≠ r_A, то система немає розв’язків, де r_A – ранг основної матриці, r - ранг розширеної матриці.

Приклад 19.

Д ослідити систему рівнянь на сумісність:

х₁ – 2х₂ + х₃ – х₄ + х₅ = -3

2х₁ - х₂ + х₃ + х₄ + х₅ = 2

-х₁ – х₂ –2х₄ = -5

3х₁ –3х₂ + 2х₃ +2х₅ = -1

1 -2 1 -1 1 -3 0 0 1 0 0 0 0 0 1 0 0 0

А = -2 -1 1 1 1 2 ~ 1 1 0 2 0 5 ~ 1 1 0 2 0 5 ~

-1 -1 0 -2 0 -5 -1 -1 0 -2 0 -5 0 0 0 0 0 0

3 -3 2 0 2 -1 1 1 0 2 0 5 0 0 0 0 0 0

0 0 1 0 0 0

~ 1 0 0 0 0 0

0 0 0 0 0 0

0 0 0 0 0 0

r_A= 2, r = 2, n = 5, r_A = r = 2 ≠ 5

В системі два незалежних рівняння: перше і друге

х₁, х₃ – базисні

х₂, х₄, х₅ – вільні

П ісля дослідження ми маємо таку систему:

х₁ + х₃ = -3 + 2х₂ + х₄ - х₅

2х₁ + х₃ = 2 + х₂ - х₄ - х₅

А = 1 1 Х = х₁ В = -3 + 2х₂ + х₄ - х₅

2 1 х₃ 2 + х₂ - х₄ - х₅

А*Х = В, Х = А^-1*В

∆ А = -1

А^* = 1 -2 - матриця із алгебраїчним доповненням

-1 1

А ^*Т = 1 -1

-2 1

А^-1 = * 1 -1 = -1 1

-2 1 2 -1

Відповідь: Х = -1 1 * -3 + 2х₂ + х₄ - х₅ =

2 -1 2 + х₂ - х₄ - х₅

= 3 - 2х₂ - х₄ + х₅ + 2 + х₂ - х₄ - х₅ = 5 - х₂ - 2х₄

-6 + 4х₂ + 2х₄ - 2х₅ - 2 - х₂ + х₄ + х₅ -8 + 3х₂ + 3х₄ - х₅

Загальний розв’язок системи:

х₁ = 5 + х₂ + 2х₄

х₃ = -8 + 3х₂ + 3х₄ - х₅

Випишемо базисний розв’язок системи. Для цього замість вільних невідомих покладаємо нулі:

х ₁ = 5

х₂ = 0

х₃ = -8

х₄ = 0

х₅ = 0

Випишемо фундаментальні розв’язки системи (одне із вільних невідомих рівне одиниці, а інші нулю):

х ₁ = 4 х₁ = 7 х₁ = 5

х₂ = 1 х₂ = 0 х₂ = 0

х₃ = -5 х₃ = -5 х₃ = -9

х₄ = 0 х₄ = 1 х₄ = 0

х₅ = 0 х₅ = 0 х₅ = 1