Тема 3: Інтегрування деяких класів функцій.

1. Інтегрування тригонометричних функцій виду:

1.1.

1.2.

1.3.

2. Інтегрування деяких ірраціональних функцій:

2.1.

2.2.

2.3.

2.4.

Інтегрування деяких тригонометричних функцій:

1.1.

а) m=2k+1 n-

sinx=t; dt=cosxdx

cos^2kx=(cos²x)^k=(1-sin²x)^k

б) n=2k+1 m-

cosx=t; dt=-sinxdx

Поступаємо аналогічно:

в) n=2k, m=2l

Знижуємо степінь використовуючи формули:

;

Приклад 1. Знайти .

Маємо:

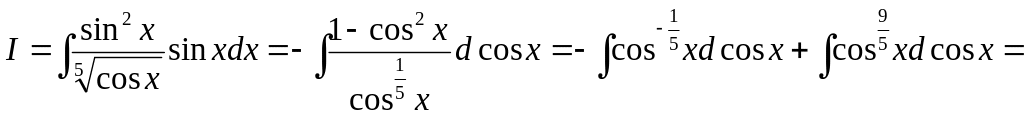
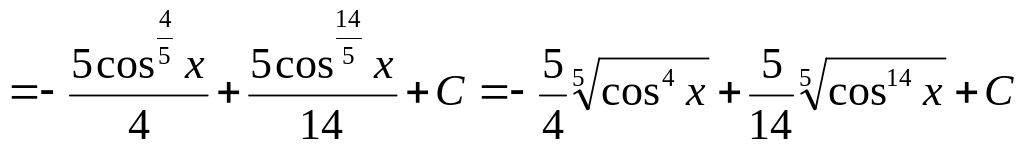
Приклад 2. Знайти інтеграл .

Оскільки

то

1.2.

Для інтегрування цих функцій використовують формули із тригонометрії:

Приклад 3. Знайти

Маємо:

1.3.

Ця функція зводиться до раціональної функції за допомогою універсальної підстановки:

Приклад 4. Знайти інтеграл .

Покладемо: . Тоді

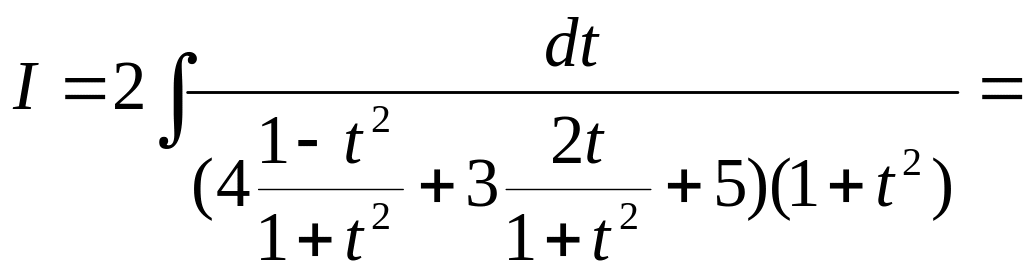
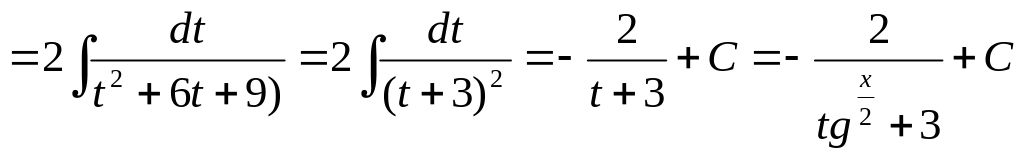
Якщо під інтегралом sinx і cosx містяться тільки в парних степенях, то зручніше використовувати підстановку tgx=t.

Інтегрування деяких ірраціональних функцій

2.1.

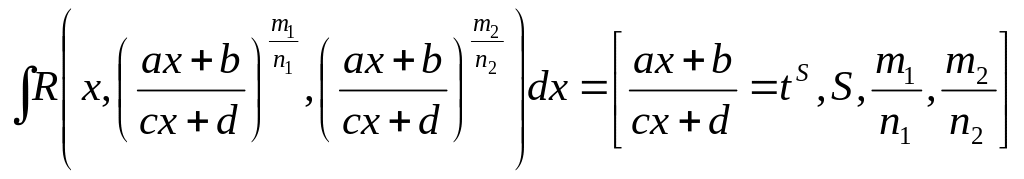
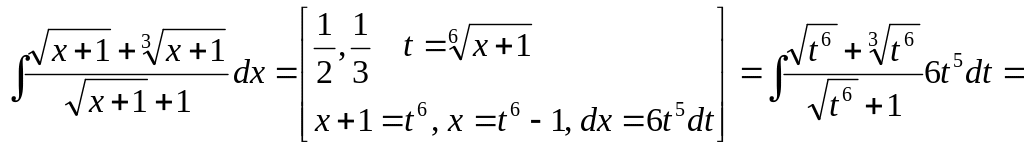
t⁷ t²-t+1

t⁷-t⁶+t⁵ t⁵+t⁴-t²-t

t⁶-t⁵

t⁶-t⁵+t⁴

-t⁴

-t⁴+t³-t²

-t³+t²

-t³+t²-t

t

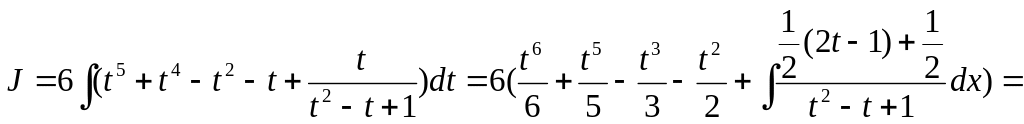
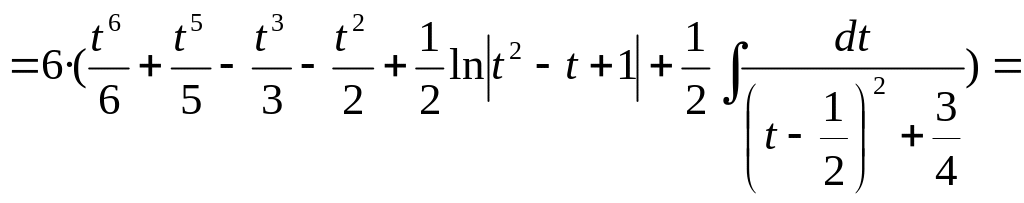
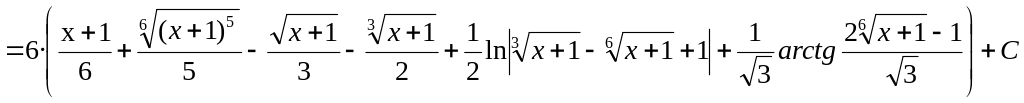
2.2.

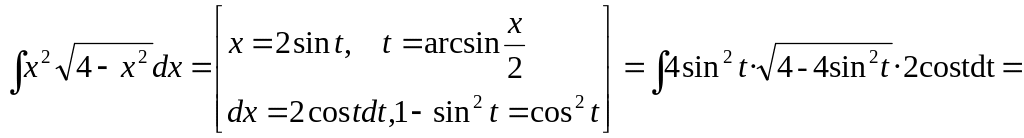
2.3.

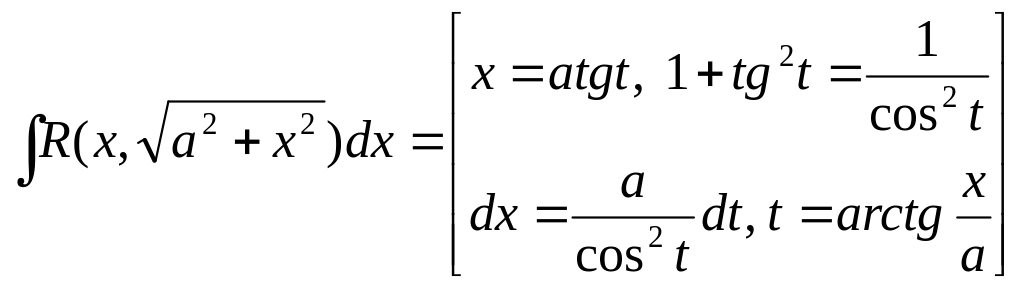
1=A₁u²(u+1)+A₂u²(u-1)+B₁u(u-1)(u+1)+B₂(u-1)(u+1)

u=0: 1=-B₂, B₂=-1

u=-1: 1=-2A₂, A₂=-

u=1: 1=2A₁, A₁=

u³: 0=A₁+A₂+B₁, B₁=0

2.4.

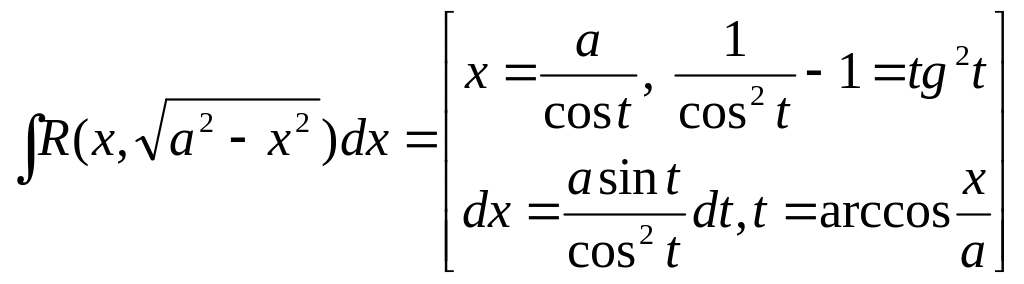
Питання для самоконтролю:

1. Коли застосовується універсальна підстановка?

2. Розказати інтегрування виразу .

3. Яка підстановка здійснюється при інтегруванні ірраціонального виразу ; ; ?

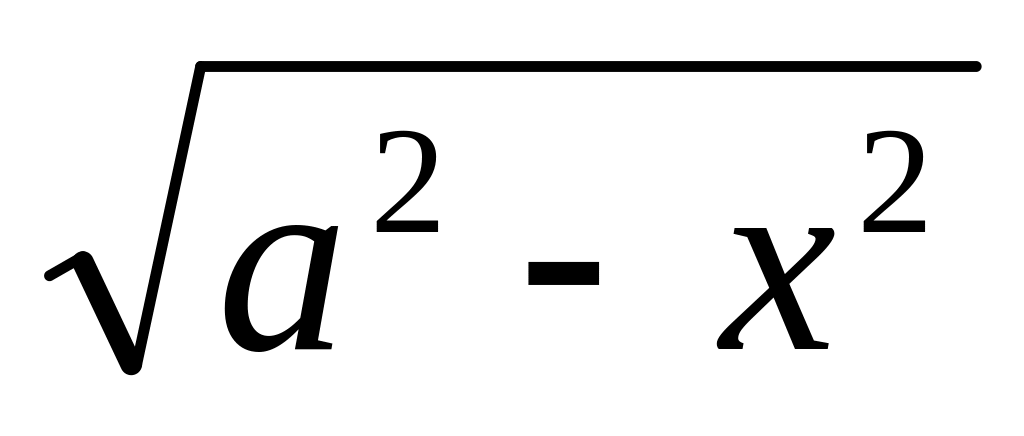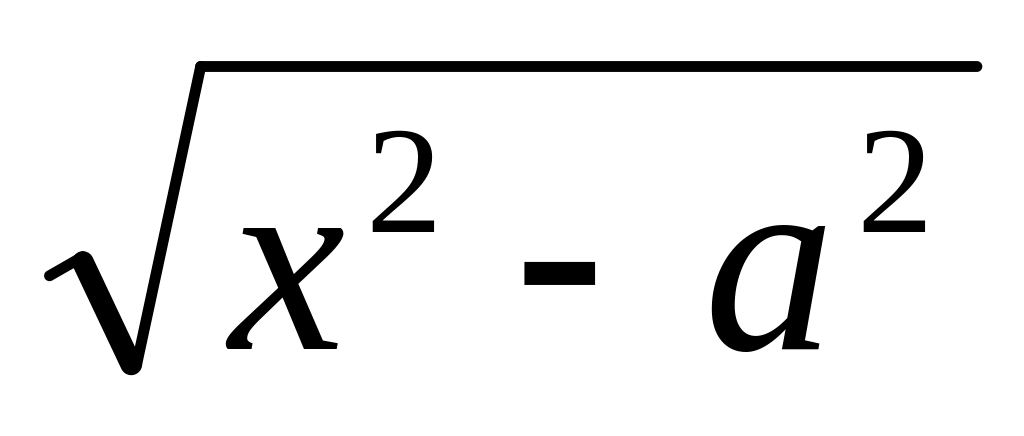Приклади для самостійного розв’язування:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

Тема 4. Диференціальні рівняння I- порядку. Задача Коші.

1. Поняття диференціального рівняння, порядок ДР, розв’язок їх.

2. ДР I-порядку. Задача Коші. Загальний розв’язок ДР. Частинний розв’язок ДР.

3. Види ДР рівнянь I- порядку і їх загальні розв’язки:

   0. ДР з відокремлюваними змінними.

   1. ДР однорідні відносно змінних.

   2. Лінійні ДР I порядку.

4. Економічні задачі на використання ДР.

5. Лінійні неоднорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами (ЛНДР).

5.1 Структура загального розвязку ЛНДР .

5.2 Побудова загального розвязку ЛОДР.

5.3 Побудова частинного розвязку ЛНДР за виглядом правої частини.

1. Означення 1.

Диференціальним рівнянням (ДР) називають співвідношення , яке зв’язуе між собою невідому функцію у(х) , її аргумент х та похідну у`, у``... Коротко записують F(x, y, y`, y``…y^(ⁿ)) = 0

Порядок ДР визначається порядком старшої похідної.

Приклад 1. y' -y³yx =sin x . Шукається у через х.

Означення 2.

Функцію у= у(х) називають розв’язком (4.1),якщо вона перетворює рівняння в тотожність (в результаті підстановки).

П риклад: y' = cos x→y=sin x-частинний розв’зок.

y=sin x+5-частинний розв’язок.

y=sin x+c y=sin x+c- загальний розв’язок.

Загальний розв’язок коли є постійна, а частинна – це коли є частинне число. Геометрично розв’язком - це інтегральна крива. Загальний розв’язок y=sin x+c - це сімейство інтегральних кривих. Геометрично ДР y=cos y задає поле напрямів на площині . Аналогічна картина отримується для довільного ДР I порядку, але можна записати F(x ,y ,y')=0 (4.2) або в такому вигляді y'=(x,y) (4.3) .

Означення 3.

З адачею Коші називають знаходження розв’язку рівняння (4.3) ,які задовольняють початкові умови : y(x₀)=y₀ (4.4). Коротко записують:

(4.5)

Геометрично це означає знайти ту криву ,яка проходить через точку з координатами (x; y).

Приклад 2. y' =cos x

y(π/6)=2

Всі розв’язки цього рівняння y= sin x+c ,але нам треба знайти лише одну точку з координатами (π/6;-2).

-2=sin π/6+C

-2=½+C => C = -2½

y= sin x-2½ - розв‘язок задачі Коші.

Означення 4.

Загальним розв’язком ДР (4.3)називають функцію y=f(x,c) (6.6), яка:

1. задовольняє рівняння (4.3)для всіх значень С;

2. для довільної початкової умови (4.4) знайдеться єдине значення С при якому функція (4.6) є розв’язком (4.3).

Приклад 3.

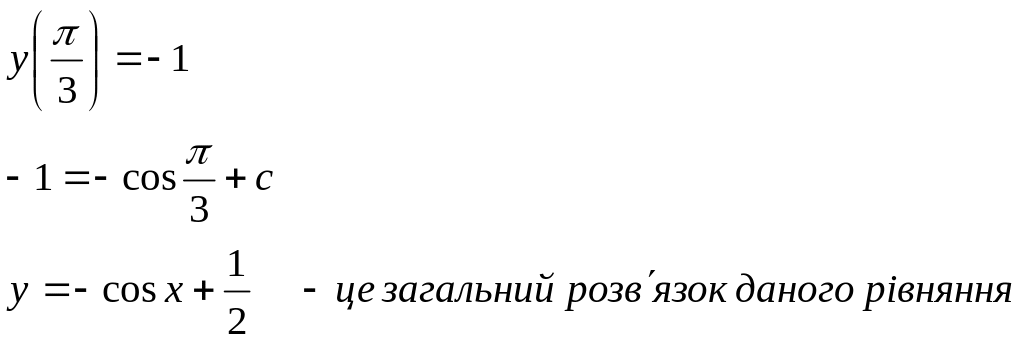
Розглянемо слідуючи ДР I-го порядку:

1. з відокремлюваними змінними;

2. однорідні відносно змінних;

3. лінійні;

4. знаходження загального розв’язку ДР змінними.

Означення 5.

Якщо ДР можна записати у вигляді y'= q₁ (x)∙q₂ (y) (4.7), то його називають рівнянням з відокремленими змінними.

П риклад 4.

- це рівняння з відокремленими змінними згідно з означенням.

Відокремимо змінні по різні сторони знака рівності

.

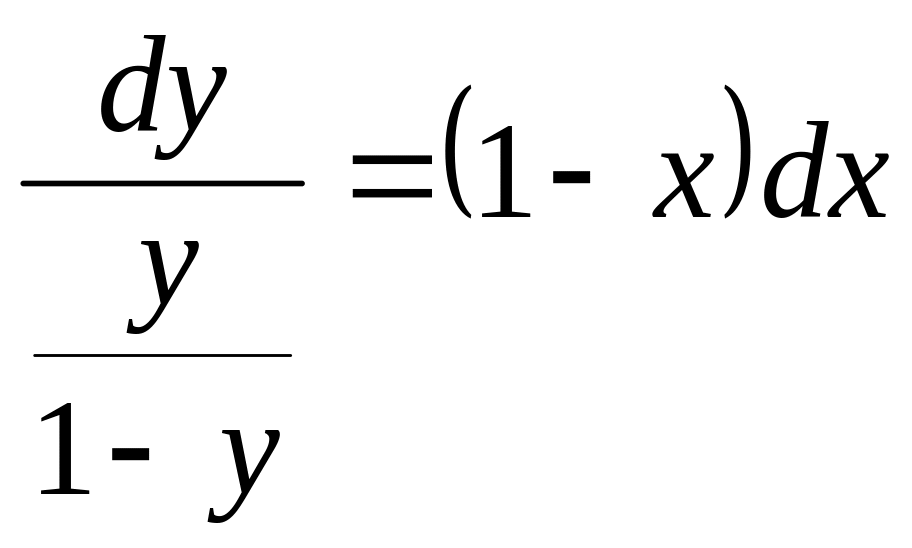
загальний інтеграл рівняння . Якщо вдається у виразити через х ,то ми отримаємо загальний розв’язок у вигляді (4.6).

Означення 6.

Функцію f(x ,y) називають однорідною відносно змінних , якщо виконується умова f(λx,λy)=f(x,y) (4.8).

Приклад 5.

f(x,y)=4x²-yx+y

f(λx,λy)=4λ²-λyλx+λy≠ f(x,y) – не однорідна.

f(x,y)=4х²- ух

f(λx,λy)= 4λx² - λyλx=λ²(4x²­yx)- однорідна II виміру.

Означення 7.

ДР (4.3) однорідне відносно змін називають , якщо функція f(x, y) є однорідною відносно змінних (4.8) нульового виміру.

Побудуємо загальний розв’язок однорідного відносно у.

y’=f(x.y) y’=

y’=(1, ) (4.11)

нова невідома

функція (6.9)

y=xu y=xu

y=u+xu’ y=u+xu’

(4.9); (4.10) (4.11) u+xu’=u+

u+xu’=f(1,u) xu’=

u’=f(1,u)-u u’= - з відокремленими зінними

u’= (f(1,u)-u)-рівняння з

відокремленими змінними

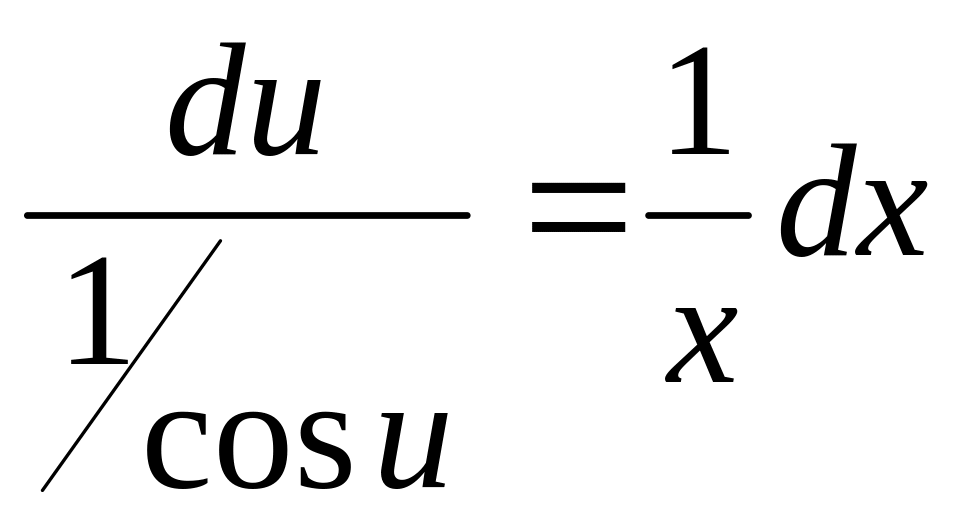
-загальний інтеграл

y=x∙arcsin (lnx+c)-загальний розв’язок.

1. Знайдемо загальний розв’язок лінійного рівняння , якщо рівняння можна записати (4.2) можна записати у вигляді.

у+p(х)у = q(х)(4.12),то його називають лінійним.

Завдання: звести його до рівняння з відокремленими змінними. Це можна зробити, якщо у записати як добуток двох невідомих функцій(придумав математик Бернулі).

y' =u(x)×v(х) (4.13)

y'=u'v +uv' (4.14)

(4.13) і (4.14)→(4.12)=> u'v + uv' + p(x)uv =q(х)

v(u'+p(x)u)+uv'=q(x)

1) u' +(x)u=0 2) uv'=q(x)

Обидва рівняння з відокремленими змінними.

Неоднорідні лінійні ДР II- го порядку зі сталим коефіцієнтом.

1. Структура загального розв’зку НЛДР (неоднорідне лінійне диференціальне рівняння) Заг. роз. =у .

2. Формули для знаходження загального розв’язку однорідного ЛДР (ОЛДР). Загальний розв`язок = у.

3. Побудова частинного розв’язку НЛДР за виглядом правої частини. Частиний розв`язок = у.

4. Задача Коші для НЛДР.

y″ +py' + qy =f(x) (4.15) називається НЛДР де р, q – числа const.

f(x) – права частина.

f(x)=0 y″+ py'+ py =0 (4.16) - називається ОЛДР.

4.1 Теорема 1.(структура у НЛДР)

Якщо у_зо- загальне розв’язок (4.16) і у_чн - частинний розв’язок, то справедлива формула у_зн = у_зо + у_чн (4.17)

Доведення:

Д ано: y_зо+py'_зо+qy_зо =0

y″_чн +py'_чн +qy_чн =f(x)

Довести ,що y″_зн +py'_зн +qy_зн =f(x)

(4.17) →(4.18) => (y_зо+y_чн)″+p(y_зо+y_чн)'+q(y_зо+y_чн) =f(x)

y″_зо+y″_чн+py'_зо+py'_чн+qy_зо+qy_чн=f(x)

0+f(x) =f(x)

Доведено.

4 .2 Теорема 2. ( Формула для знаходження у )

Якщо відомі корені характеристичного рівняння λ² +pλ +q=0 (4.19), то у знаходиться за формулами:

(4.20) 1) λ₁≠λ₂,

(4.21) 2) ₁=₂,

(4.22) 3)_1.2=+і, i=

i²= -1

4.3 Теорема 3. (Формули для знаходження у_чн)

Я кщо права частина має вигляд f(x)=e^x(p_n(x) cosx+ Q_m(x) sin x) (4.23) то у_чн= х^sе^х(p_e(x)) cos x+Q_e(x)sin x (4.24), де

і – число що відповідає правій частині (4.23).

S – число яке показує скільки раз число і зустрічається серед коренів характеристичного рівняння е = max(n,m).

~ - многочлени з невідомими коефіцієнтами.

Знайти загальний розв’язок рівняння.

Приклад 5.

1)

2)

- згідно з (4.24)

Знайдемо А так, щоб дана функція була розв`язком неодноріного рівняння. Для цього підставимо її в рівняння:

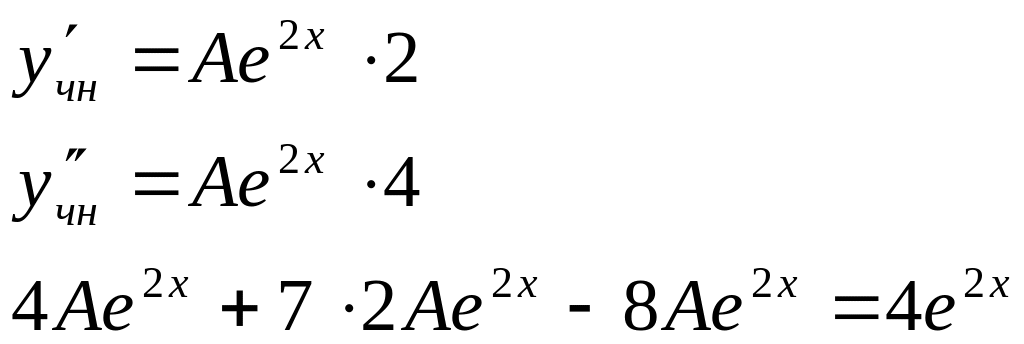
4А+14А-8А=4

10А=4

3)

Приклад 6.

1)

2)

, s=0

C=2

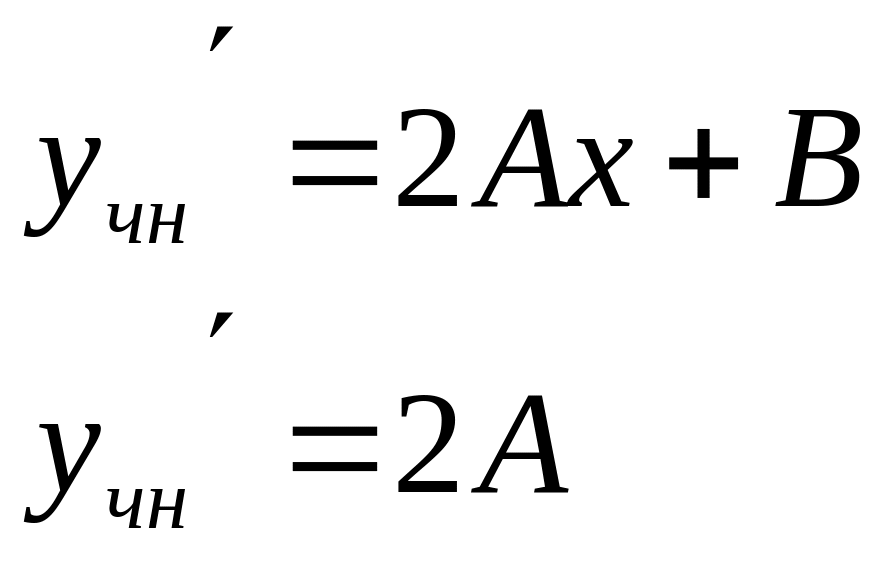
2А-6(2Ах+В)+9( )=

: 9А=1, А=

х : -12А+9В=0 -4В+3В=0 В=

: 2А-6В+9С=5 С= (5-2А+6В)= .

= +