Другий семестр Змістовний модуль 3
Тема 1. Невизначений інтеграл, основні методи інтегрування
Поняття первісної і невизначеного інтеграла.
Основні властивості інтеграла.
Основні методи інтегрування:
4.1. безпосереднє інтегрування,
4.2. заміна змінної інтегрування (метод підстановки),
4.3. інтегрування частинами.
Означення
1. Функція
f(x)
називається первісною
для функції f(x),
якщо
=
f(x)
(1.1).
Приклад. Нехай f(х)=1, знайти f(x)=x, f(x)=sin x z(x)= - cos x,
f(x)=
z(x)=tg
х.
Для кожної функції, якщо існує одна первісна, то існує безліч, які відрізняється між собою на постійний доданок.
Означення 2 Невизначеним інтегралом для функції f(x) називається сукупність всіх її первісних і записують так:
(1.2),
де f(x) – підінтегральна функція, dx – диференціал аргументу.
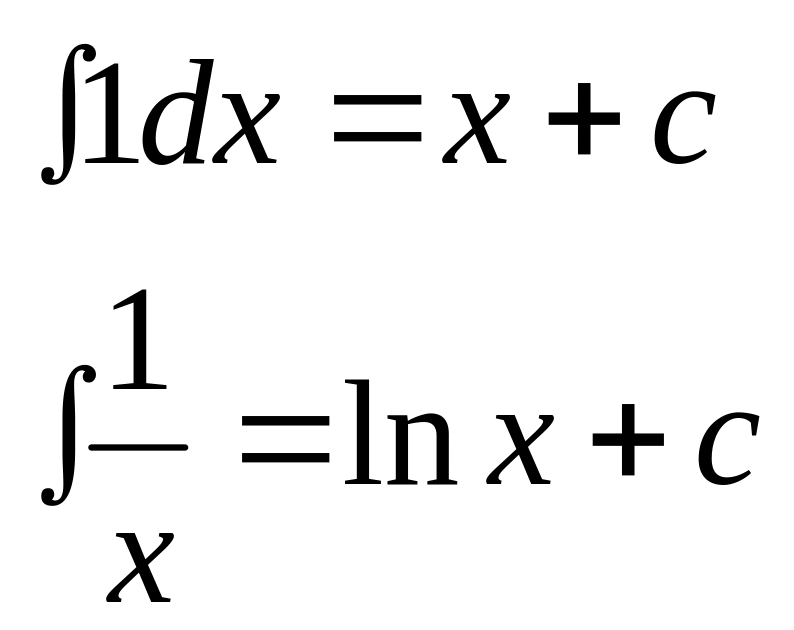
Властивості
інтеграла:
1.
2.
Зв’язок між похідною і інтегралом.
3.
Доведення:
4.
Доведення:
З властивостей 3,4 видно, що дії інтегрування і диференціювання взаємно обернені.
5.Якщо , то
(1.3)
Доведення:
Таблиця
інтегралів
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
Наприклад:
Таблиця інтегралів справедлива, якщо в ролі букви х виступає будь-яка інша буква.
1.
2.
3.
4.
5.
6.
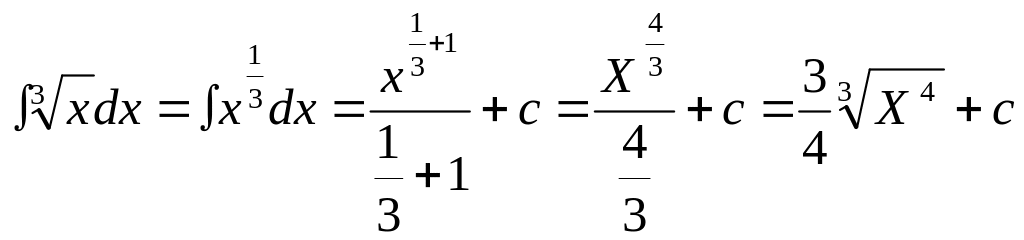
7.
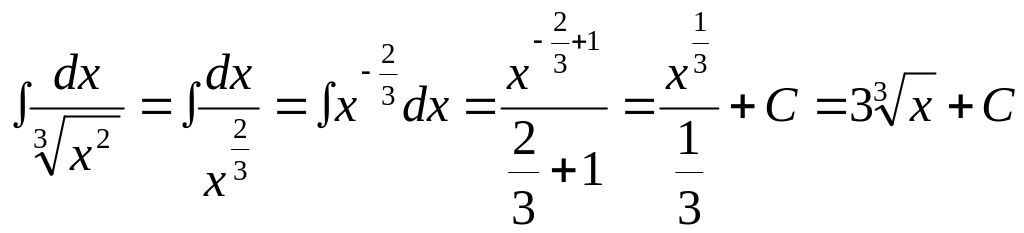
8.
Приклади на формулу (1.3).
1.
2.
3.
4.
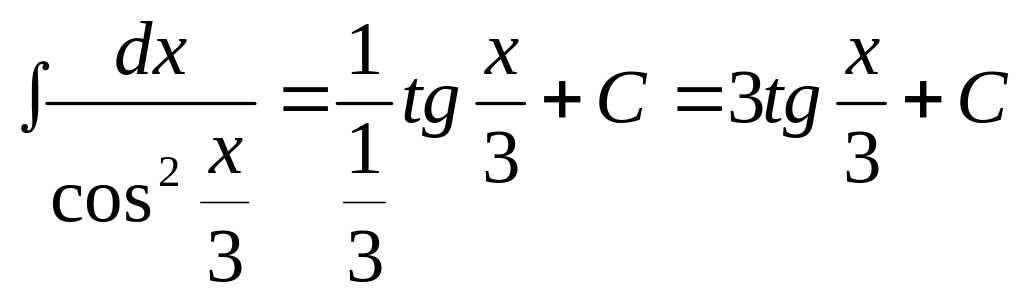
5.
6.
7.
8.
9.
Основні
методи інтегрування
Суть
методу безпосереднього інтегрування:
даний інтеграл за допомогою елементарних
перетворень:
;
;
;
;
і т. д. і властивостей інтеграла (1.2)
зводиться до суми різних табличних
інтегралів.
1.
2.
3.
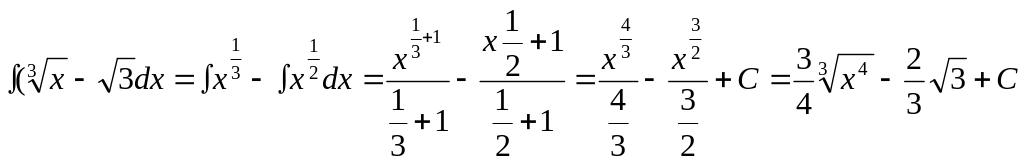
4.
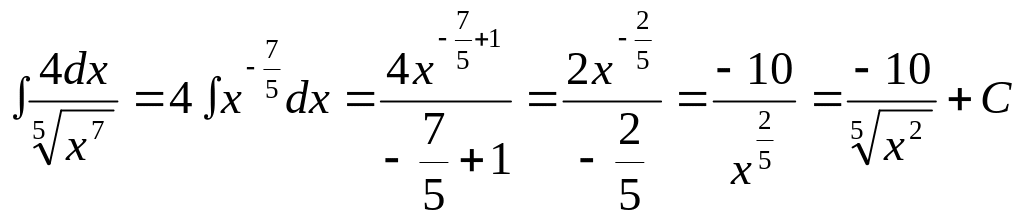
5.
6.
4.2.Заміна змінної інтегрування. 2 способи заміни інтегрування.
А)
Теорема 1.Якщо
невизначений інтеграл має вигляд
,
то він зводиться до табличного за
допомогою заміни змінної інтегрування,
тобто підставки
- нова зміна інтегрування, записують це
так:
(1.4).
1.
2.
3.
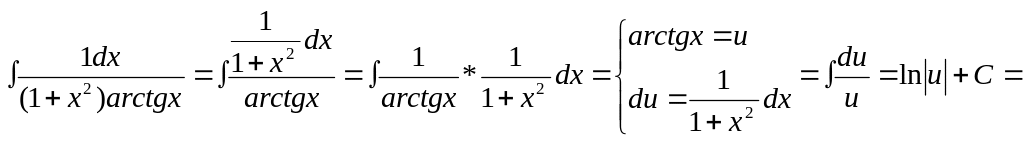
Б) Теорема2. Якщо інтеграл не є табличним інтегралом і не зводиться до табличного за допомогою елементарних перетворень, то робимо підстановку
,
t
– нова змінна, записується так:
(1.5)
В) Інтегрування частинами здійснюється за формулою
,
(1.6),
де
,
.
Формула (1.6) використовується у випадку, коли під інтегралом є добуток або частка суттєво різних функцій
,
Також
ця формула використовується для
інтегралів, яких немає у таблиці
Зауваження.
Частіше всього в ролі
вибирають степеневу функцію, але не
завжди. Наприклад,
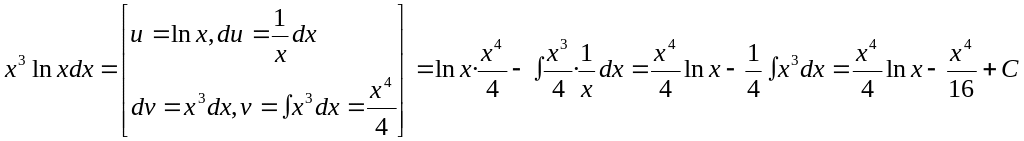
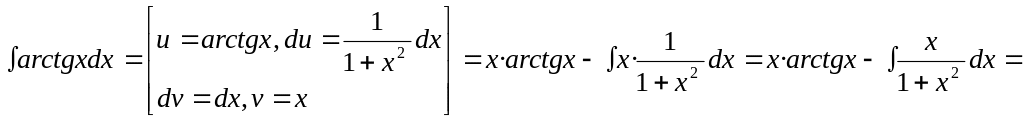
Питання для самоконтролю:
Як здійснюється заміна змінної інтегрування?
Назвіть формулу інтегрування частинами.
Коли застосовуються формули інтегрування частинами?
Суть безпосереднього інтегрування.
Назвіть властивості невизначеного інтеграла.
Означення невизначеного інтеграла.
Завдання для самостійного розв’язування:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.