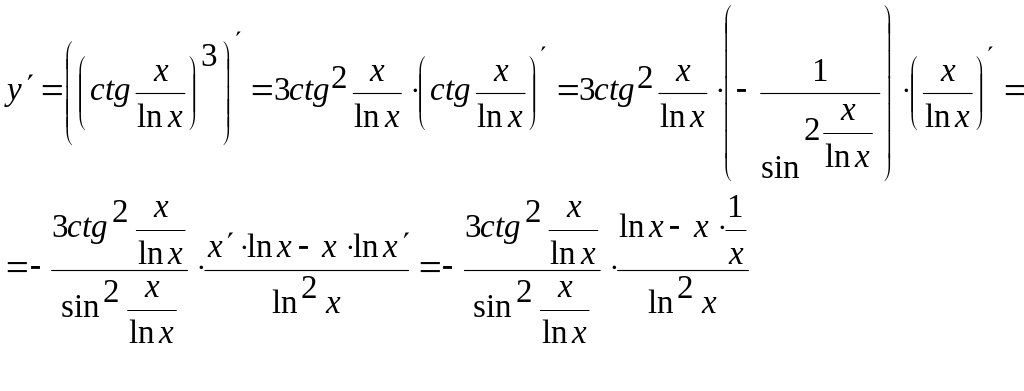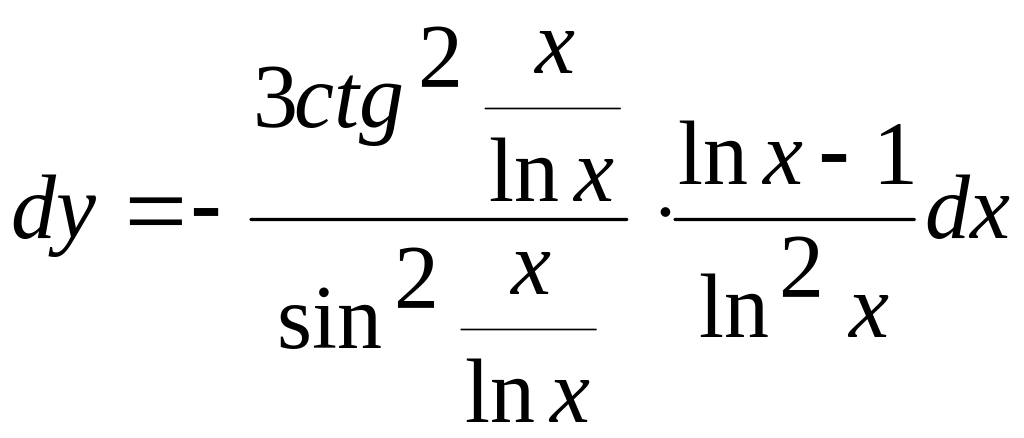- •З дисципліни
- •I семестр
- •II семестр
- •Перший семестр Змістовний модуль №1 тема 1. Системи лінійних алгебраїчних рівнянь і методи їх розв’язання
- •3. Властивості визначників:
- •5. Теорема Крамера:
- •Множення матриць
- •Додавання матриць
- •Віднімання матриць
- •Добуток матриці на число
- •7. Обернена матриця
- •8. Матричний спосіб розв’язання систем (слар)
- •9. Ранг матриці
- •10. Теорема Кронекера – Капеллі.
- •11. Метод Джордано - Гаусса – універсальний метод
- •Питання для самоперевірки.
- •Задачі для самостійного розв’язання.
- •Тема2. Елементи векторної алгебри. Вектори в просторі r3.
- •Питання для самоперевірки.
- •Задачі для самостійного розв’язання.
- •Тема 3. N-вимірний лінійний простір. Перехід від одного базиса до іншого.
- •Питання для самоперевірки.
- •Задачі для самостійного розв’язання.
- •Змістовний модуль 2. Тема 4. Аналітична геометрія на площині. Пряма лінія на площині.
- •Питання для самоперевірки.
- •Задачі для самостійного розв’язання.
- •Тема 5. Криві другого порядку.
- •Тема 6. Деякі елементи аналітичної геометрії в просторі План
- •4.2. Канонічні рівняння прямої
- •4.3 Параметричні рівняння прямої
- •Контрольні питання
- •Завдання для самостійного виконання
- •Тема 7. Вступ в математичний аналіз. Поняття границі та методи її знаходження.
- •1 Означення функції.
- •4 Основні властивості границі змінної величини.
- •6 Техніка знаходження границь.
- •7 Перша чудова границя
- •Питання для самоперевірки
- •Завдання для самостійного розв’язання
- •Тема 8.Неперервність функції. Теореми про неперервні функції.
- •4 Властивості:
- •Питання для самоперевірки
- •Завдання для самостійного розв’язання
- •Тема 9. Поняття похідної. Похідні функцій, заданих явно, неявно, параметрично.
- •Задачі, які привели до поняття похідної
- •Означення похідної та її геометричний зміст
- •Зв’зок диференційованості функції з неперервністю
- •Основні правила диференційювання
- •6. Поняття диференціала функції та його застосування до наближених обчислень. Геометричний зміст диференціала
- •7. Похідні вищих порядків
- •2. Одержане алгебраїчне рівняння розв’язуємо відносно відомого :
- •9. Похідна степенево-показникової функції.
- •Похідна функції, заданої параметрично.
- •Питання для самоперевірки
- •Завдання для самостійного розв’язання
- •Контрольні завдання
- •Тема 10. Застосування похідних до дослідження функції.
- •Завдання для самостійного розв’язання.
- •Другий семестр Змістовний модуль 3
- •Тема 1. Невизначений інтеграл, основні методи інтегрування
- •Тема 2. Інтегрування дробово – раціональних функцій.
- •Тема 3: Інтегрування деяких класів функцій.
- •Тема 4. Диференціальні рівняння I- порядку. Задача Коші.
- •Означення 1.
- •Питання для самоперевірки
- •Завдання для самостійного виконання:
- •Змістовний модуль 4 Тема 5. Функція двох змінних
- •Тема 6. Екстремум функції двох змінних. Спосіб найменших квадратів.
- •Приклад 1.
- •Тема 7. Числові та степеневі ряди.
- •Питання для самоконтролю.
Означення похідної та її геометричний зміст
Похідною
функції y
= f(x)
за аргументом х називають границю
відношення приросту функції ∆у до
приросту аргументу ∆x, коли ∆x довільним
чином прямує до нуля. Якщо ця границя
існує, то її позначають через f´(x),
або у´, або у´х або
![]() ,
або
,
або
![]()
Математично похідна функції визначається за формулою:
![]()
Механічний зміст похідної: похідна S´(t) є величиною миттєвої швидкості в момент t тіла, що рухається за законом S = S(t).
Геометричний зміст похідної: похідна f´(x) дорівнює кутовому коефіцієнту дотичної до графіка функції y = f(x) в точці з абсцисою х.
Економічний зміст похідної: похідні V´(x), D´(x) та Р´(х) дорівнюють маргінальній вартості, доходу, прибутку, відповідно.
Зв’зок диференційованості функції з неперервністю
Якщо
функція y
= f(x)
диференційована в деякій точці
![]() ,
то вона в цій точці неперервна:
,
то вона в цій точці неперервна:
Доведення: якщо y = f(x) диференційована в , то існує
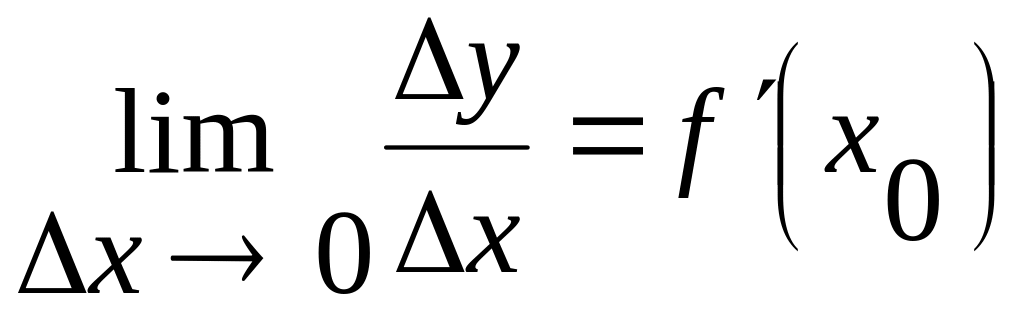
В силу того, що границя змінної величини відрізняється від самої змінної лише на нескінченно малу величину , то маємо:
![]()
Оскільки
![]() - стала, то з властивостей нескінченно
малих випливае,що
∆x
і
- стала, то з властивостей нескінченно
малих випливае,що
∆x
і
![]() є нескінченно малими величинами. Звідси
∆у→0, коли ∆x→0, тобто функція y
= f(x)
неперервна в точці
.
є нескінченно малими величинами. Звідси
∆у→0, коли ∆x→0, тобто функція y
= f(x)
неперервна в точці
.
Наслідок: З цієї теореми випливає,що неперервність функції є необхідною умовою диференційованості функції. Це означає, що в точках розриву функція не має похідної, тобто вона не диференційована.
Основні правила диференційювання
1. Похідна постійної величини С дорівнює нулю, тобто С´=0
2.
Якщо кожна із функцій
![]() (n
– нескінченне число) диференційована
в деякій точці х, то її алгебраїчна сума
також є диференційованою в цій точці,
причому похідна алгебраїчної суми цих
функцій дорівнює такій самій алгебраїчній
сумі їх похідних, тобто
(n
– нескінченне число) диференційована
в деякій точці х, то її алгебраїчна сума
також є диференційованою в цій точці,
причому похідна алгебраїчної суми цих
функцій дорівнює такій самій алгебраїчній
сумі їх похідних, тобто
![]()
3. Якщо кожна з функцій u(x) та V(x) диференційована в точці х, то добуток цих функцій також має похідну в точці х, причому цю похідну знаходять за формулою:
![]()
4. Якщо u(x) та V(x) мають похідні в точці х і V(x) 0, то частка цих функцій також має похідну в точці х, яку знаходять за формулою:

5.
Якщо у=f(u),
u=![]() (x)
і функції f
та
диференційовані функції своїх аргументів,
то існує похідна по складної функції
у, причому вона дорівнює добутку похідної
функції у по проміжному аргументу u
та похідної функції
по аргументу х, тобто
(x)
і функції f
та
диференційовані функції своїх аргументів,
то існує похідна по складної функції
у, причому вона дорівнює добутку похідної
функції у по проміжному аргументу u
та похідної функції
по аргументу х, тобто
![]()
Таблиця похідних
![]()
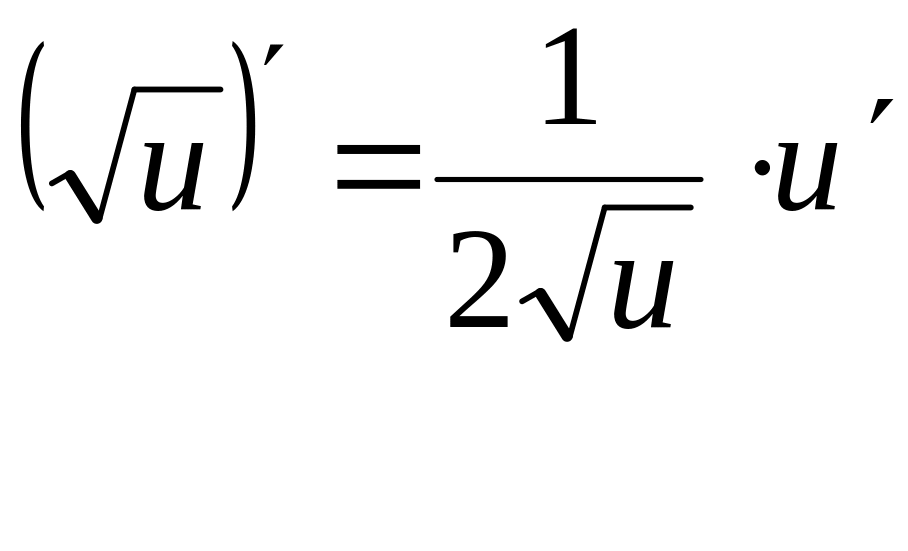
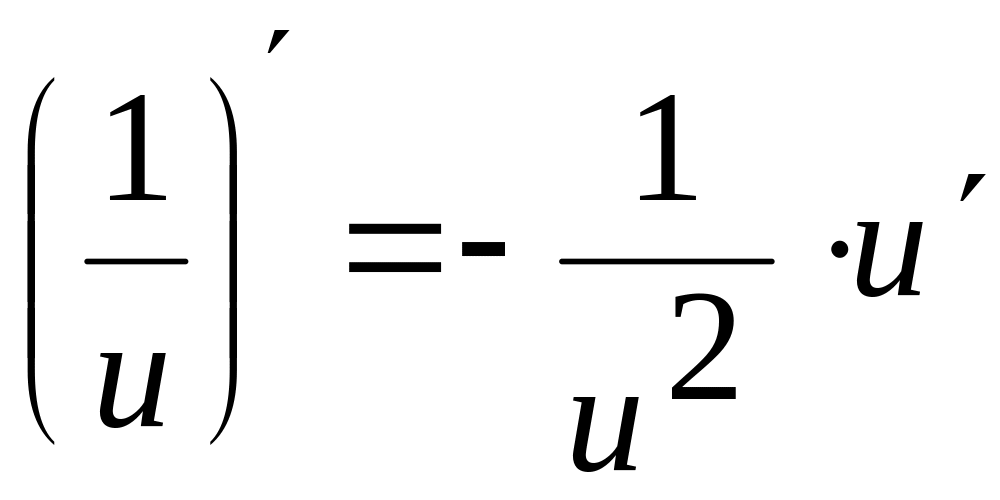
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6. Поняття диференціала функції та його застосування до наближених обчислень. Геометричний зміст диференціала
Розглянемо
формулу
![]() (9.1)
(9.1)
![]()
![]() (9.2)
(9.2)
![]()
Диференціалом функції y=f(x) називають головну лінійку по ∆x частину приросту (11.2) і записують так:
![]() ;
;
![]() (9.3)
(9.3)
![]()
![]() (9.4)
(9.4)
Застосування
до наближених обчислень. Порівняння
![]() y
з dy
показє, що
y
з dy
показє, що
![]()
Звідси
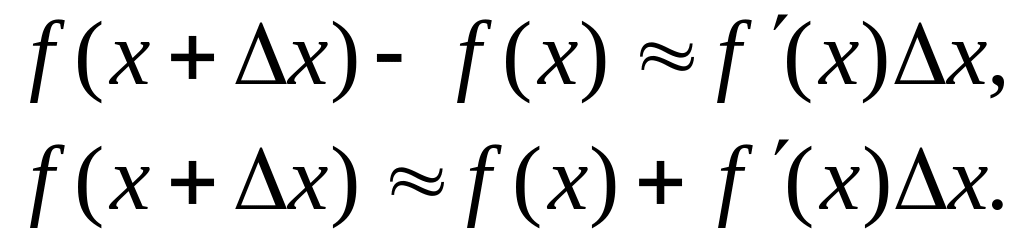
Ця формула застосовується для наближеного обчисленя значень функції при малому прирості x незалежної змінної x.
Геометричний зміст диференціала. Геометрично диференціал – це приріст ординати дотичної до кривої, проведеної в точці М(x,y).
Приклад:
знайти диференціал функції
![]()
![]()