Правило смесей
Так как свойства КМ определяются свойствами составляющих его матрицы и арматуры, то необходимо установить зависимость свойств КМ от концентрации (количества) этих составляющих.
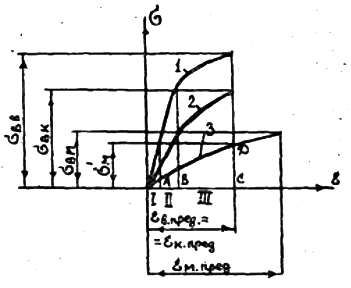
Рис.2.4. Диаграмма растяжения волокон (1), матрицы (3) и однонаправленного КМ (2)
Вернемся к модели однонаправленного трансверсально изотропного КМ и рассмотрим характер его деформации под действием растягивающей нагрузки, приложенной параллельно оси волокон (рис. 2.4).
Предположим, что матрица более пластична (м.пред>в.пред) и имеет меньший модуль упругости, чем волокна (модуль упругости характеризуется тангенсом угла наклона линейного участка кривой к оси деформаций).
В общем случае кривая 2 растяжения КМ должна состоять из трех участков: I – матрица и волокна деформируются упруго; II – матрица переходит в упругопластическое состояние, а волокна продолжают деформироваться упруго; III – оба компонента системы находятся в состоянии пластической деформации. В зависимости от свойств компонентов КМ участки II и III на кривой могут отсутствовать.
Примем, что прочность связи на границе раздела волокно-матрица достаточна для того, чтобы обеспечить совместную деформацию компонентов вплоть до разрушения, т.е. что в = м = к.
Поэтому сумма нагрузок, приходящихся на матрицу и волокна, равна внешней нагрузке, воспринимаемой КМ.
Тогда, используя уравнение. (2.6), предел прочности КМ σвк можно выразить в виде линейной функции от объемной доли волокон Vв:
(2.19)
здесь:
– среднее
значение предела прочности волокон при
растяжении;
– напряжение в
матрице в момент разрыва волокон
(рис. 2.3);
Vм, Vв – объемная доля матрицы и волокна в КМ, соответственно.
Следует подчеркнуть, что м – это не предел прочности матрицы, а напряжение, соответствующее такой ее деформации, которая равна предельной деформации волокон до разрушения в пред. Чтобы определить м, нужно из точки С (рис. 2.4.), соответствующей относительной деформации разрушения волокон в, восстановить перпендикуляр. Ордината точки Д пересечения этой прямой с кривой 3 будет равна м. Для неупрочняющихся пластичных матриц м можно принять равной пределу текучести матрицы.
Уравнение (2.19) обычно называют уравнением смесей (правилом смесей) или уравнением (правилом) аддитивности.
На практике во многих случаях допущения, принятые для вывода этого уравнения, нарушаются. Волокна могут разрушаться не одновременно, а последовательно из-за наличия в них дефектов. Наиболее дефектные волокна разрушаются при малых напряжениях, далеких от предела прочности; волокна с меньшей дефектностью разрушаются при несколько больших напряжениях; а в целом прочность КМ будет меньше рассчитанной по правилу смесей. То же можно сказать, когда матрица имеет недостаточный запас пластичности, что приводит к появлению трещин на границе раздела и в теле матрицы и к преждевременному разрушению КМ в целом.
Однако возможны случаи, когда реальная прочность однонаправленного армированного материала оказывается выше, чем предсказывается правилом аддитивности. Например, если пластичная матрица армирована пластичными волокнами, то при растяжении КМ связь между волокнами и матрицей затрудняет образование шейки на волокнах. В результате волокна в КМ деформируются более равномерно, чем при их растяжении в чистом виде (без матрицы). В последнем случае после образования шейки вся дальнейшая деформация концентрируется в ней, вызывая быстрое разрушение. Таким образом, задержка в образовании шейки в конечном итоге увеличивает условный предел прочности волокон и композиции в целом. Тем не менее, уравнение (2.19) можно использовать для оценочных расчетов, так как во многих случаях (при условии получения КМ по оптимальным технологическим режимам) отклонение расчетных значений прочности от экспериментальных невелико.