Свободная поверхностная энергия тел

Металл	Свободная поверхностная энергия, Т-Г, эрг/см2	Метод измерения	Температура измерения, t, С	Т-Г/Ж-Г
Пирографит (200) Пирографит (200) Окись магния MgO (100) Кремний Si (111) Титан Ti Цирконий Zr Ниобий Nb	1500 1800 1200 1240 1700 1850 2100	И.В. Обреимова Гилмана » » Нулевой ползучести То же » »	20 20 20 20 1600 1800 2250	– – – 1,32 1,22 1,23 1,02

Разновидностью метода Обреимова является следующий способ определения _Т-Г. В предварительно нанесенную трещину вставляют клин и определяют «критическую» силу, необходимую для дальнейшего развития трещины. Тогда

,

где:

F – критическая сила;

L – глубина первоначальной трещины;

b – ширина образца;

h – толщина отщепляемой части.

В отличие от метода Обреимова, этот способ неравновесный, но его применение исключает опасность адсорбции из атмосферы на вновь образующиеся поверхности вследствие быстрого проведения опыта.

Широкое распространение получил метод расщепления Гилмана, в котором к концам предварительно расщепленного образца прикладывается растягивающая сила. Как и в предыдущем способе, измеряется критическая сила

,

где:

F – критическая сила раскалывания;

L – длина предварительно созданной трещины;

Е – модуль упругости;

b – ширина образца;

h – полутолщина.

Этим методом определяли поверхностную энергию тугоплавких окислов (табл. 4.5).

Для определения свободной поверхностной энергии пластичных твердых тел, в частности металлов, применяется метод Таммана – Удина. Он заключается в том, что тонкая фольга или проволока нагревается до температуры, близкой к температуре плавления металла. Силы поверхностного натяжения стремятся уменьшить свободную поверхность металла, что приводит к уменьшению длины фольги или проволоки. Действие поверхностных сил можно скомпенсировать наложением внешней нагрузки. Чаще всего к образцам подвешивают грузы различной массы. Когда удлинение равно нулю

,

где:

Р – нагрузка;

b – ширина фольги.

Подобным методом определяли _Т-Г титана, циркония и ниобия (табл. 4.5). Отношение _Т/_Ж для титана оказалось равным 1,27, что несколько превышает теоретическую оценку этой величины, выполненную С.Н. Задумкиным (1,15).

4.6.3. Свободная поверхностная энергия на границе твердое тело - жидкость

К сожалению, до настоящего времени отсутствуют надежные экспериментальные методы определения свободной поверхностной энергии на границе твердое тело - жидкость. Однако отдельные попытки, экспериментального определения межфазной энергии известны. В.И. Лихтман и др. измерили _Т.Ж методом нулевой ползучести, обнаружив резкое снижение поверхностного натяжения цинка на границе с жидким Sn (до 200 мДж/м²) и не слишком большое ( 100 мДж/м²} снижение его на границе с расплавленным Pb.

В.И. Костиковым и др. предпринята попытка определить свободную межфазную энергию на границе жидкий кремний - пирографит для случая, когда капля жидкого металла на поверхности твердого тела имеет сколь угодно малый равновесный краевой угол. Для определения _Т.К применяли метод подъема металла между двумя плоскопараллельными пластинами (рис. 4.15), теория которого изложена ниже.

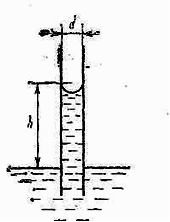
Рис. 4.15. Схема методы определения межфазной свободной поверхностной энергии на

границе твердое тело - жидкость

Уравнение Лапласа можно записать следующим образом:

, (4.31)

где:

Р₁ и Р₂ – давления с вогнутой и выпуклой сторон мениска соответственно;

_Ж.Г – свободная поверхностная энергия жидкости;

R₁ и R₂ – главные радиусы кривизны.

Для случая двух параллельных пластин одни из радиусов кривизны равен бесконечности, и уравнение (4.31) можно записать в виде:

,

но

,

где:

 – плотность жидкости;

g – ускорение силы тяжести;

h – высота подъема металла между пластинами.

Радиус кривизны R определяется уравнением:

,

где:

d – расстояние между пластинами;

 – краевой угол смачивания.

Следовательно:

.

Или, принимая во внимание уравнение (4.18) можно окончательно получить:

. (4.32)

Возможен также, и другой вывод уравнения (4.32). Действительно, если предположить, что ширина пластины а, то движущая сила F при подъеме металла между двумя пластинами определяется очевидным уравнением:

. (4.33)

С другой стороны, сила тяжести Р при подъеме металла на высоту h равна:

,

где:

 – плотность металла;

g – ускорение силы тяжести;

d – расстояние между пластинами.

В момент достижения максимальной высоты Р = F легко получить:

,

откуда

Таким образом, если измерить высоту подъема металла между параллельными пластинами при заданном расстоянии, можно определить значение (_Т.Г – _Т.Ж), а зная свободную поверхностную энергию твердого тела, легко рассчитать свободную межфазную энергию на границе твердое тело - жидкость, В качестве жидких металлов использовали кремний и сплавы на основе кремния с добавками титана и циркония.

Сплавы из кремния полупроводниковой чистоты и иодидных титана и циркония приготавливали двойной дуговой плавкой на медном водоохлаждаемом поду в атмосфере очищенного аргона.

В качестве твердого тела применяли пирографит марки П2100А, для которого методом Обреимова была предварительно определена свободная поверхностная энергия (_Т.Г. = 350 мДж/м²).

Кремний и его сплавы расплавляли в алундовых тиглях. Размеры тиглей выбирали так, чтобы исключить эффект влияния стенок тигля на поднятие металла между пластинами, Параллельные пластины из пирографита с фиксированным и измеренным расстоянием между ними погружали в расплавленный металл и выдерживали в течение 1 ч при температуре, превышающей на 50-100°С температуру плавления металла.

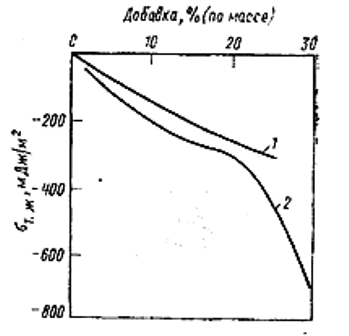
Рис. 4.16. Влияние добавки легирующих элементов на _Т.Ж на границе сплав - пирографит:

1 – сплав Si-Ti; 2 – сплав Si-Zr

Опыты проводили в печи ТВВ-4 в вакууме 6,67 сПа. Высоту подъема жидкого металла между пластинами определяли после опыта. Расстояние между пластинами варьировали от 2 до 4 мм.

Во всех случаях за высоту подъема металла принимали расстояние от уровня металла в тигле до максимальной точки подъема металла.

Значения _Т.Ж на границе жидкий кремний (сплав) - пирографит для указанных металлов и сплавов при температуре опыта 1500°С, d = 0,15 см и _Т = 275 мДж/м² приведены ниже:

	Si	Si + 5% Ti	Si + 15% Ti	Si + 25% Ti
Т.Г – Т.Ж, мДж/м2	300	400	500	600
Т.Ж, мДж/м2	–25	–125	–225	–325
h, см	1,7	2,0	2,5	3,0

	Si + 10% Zr	Si + 20% Zr	Si + 30% Zr
Т.Г – Т.Ж, мДж/м2	500	600	1000
Т.Ж, мДж/м2	–225	–325	–725
h, см	2,5	3,0	4,0

Величины свободной поверхностной энергии пирографита при температурах опытов рассчитывали с использованием температурного коэффициента k, равного 0,05 мДж/(м²К).

Оказалось, что свободная межфазная энергия на границе кремний - пирографит близка к нулю.

При увеличении содержания титана и циркония в кремнии (рис. 4.16) свободная межфазная энергия на границе с пирографитом понижается, но не так резко, как это можно было бы ожидать. Лишь при содержании 30% циркония в кремнии наблюдается довольно значительное понижение _Т.Ж. Недостаточно высокая межфазная активность титана и циркония в кремниевых расплавах па границе с пирографитом, по-видимому, объясняется сильным взаимодействием этих атомов с кремнием в объеме с образованием комплексов типа Ti_xS_y и Zr_xSi_y. Это предположение подтверждается результатами рентгеноструктурного исследования расплава в тиглях после опытов. Во всех случаях обнаружено наличие силицидов: TiSi₂, Ti₅Si₃, ZrSi₂, Zr₅Si₃. Следует далее отметить, что полученные отрицательные значения межфазной энергии реализуются только в процессе поднятия металла между пластинами, т.е. речь идет о динамической межфазной энергии. В условиях равновесия межфазная энергия может быть как угодно близка к нулю, но обязательно положительна. В наших экспериментах столб жидкости поднимается под действием движущей силы (_Т.Г – _Т.Ж), причем значение _Т.Ж во времени изменяется от больших отрицательных значений до некоторой положительной величины. Однако столб жидкости, поднявшись между пластинами, не может опуститься в результате повышения межфазной энергии. Поэтому здесь определены эффективные значения _Т.Ж, которые оказались отрицательными, за исключением _Т.Ж на границе жидкий кремний - пирографит.