Диффузия в образце конечных размеров

Диффузия в пластину толщиной l_n с нулевой начальной концентрацией и постоянной концентрацией С₀ на концах (концы пластины совпадают с плоскостями х = 0 и х = l_n) описывается уравнением

.

При для практических расчетов ограничиваются одним членом ряда

.

Количество вещества, проникающего в пластину за время t через поверхность S, определяется из соотношения

.

Если вещество уходит из пластины, имевшей постоянную начальную концентрацию, через границы (х = 0, х = l_n), на которых поддерживается нулевая концентрация, то

.

4.5.3. Диффузия в среде со сферической симметрией

Распределение концентрации С вещества, диффундирующего в сферически-симметричном слое, определяется выражением

,

где:

С₁ – концентрация на внутренней границе сферического слоя (r = r₁) в течение всего времени диффузии;

С₂ – концентрация на внешней границе сферического слоя (r = r₂) в течение всего времени диффузии. Эту формулу используют при больших значениях t (точнее, больших параметрических числах Фурье Dt/( r₁ – r₂)². При (Dt/( r₁ – r₂)²) << 1 удобнее пользоваться выражением

,

где:

erfc означает 1 – erf.

Количество вещества, поглощенного или выделенного за время t в процессе диффузии из сферически-симметричного слоя при нулевой начальной концентрации (С₀ = 0) и при больших значениях t, определяется выражением

.

При малых диффузионных числах Фурье количество поглощенного диффундирующего вещества рассчитывается по более удобной формуле

,

где:

.

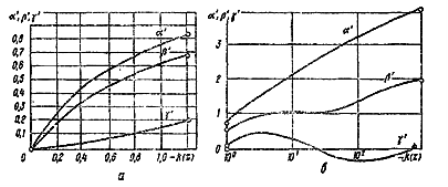
Рис. 4.6. Зависимость коэффициентов , ,  от параметра k(z) при малых (а) и при

больших (б) значениях k(z)

При униполярном растворении сферического включения, когда диффузия внутри его пренебрежимо мала и его растворение определяется диффузией в матрице неограниченных размеров, изменение относительных размеров включения во времени описывается рядом , где ₀ и  – соответственно начальный и текущий радиус включения; , ,  – безразмерные коэффициенты; – безразмерное время. Предполагается, что на поверхности включения сохраняется равновесная для данной температуры концентрация С₁, определяемая из диаграммы состояния. Начальный радиус включения ₀, текущий радиус – (t). Вдали от включения сохраняется исходная концентрация С₀, т. е, . Непосредственно у поверхности сферической частицы С ((t), t) = С₁. Начальное условие С (r, 0) = С₀.

Коэффициенты , ,  являются функцией одного параметра k(z) = (C₁ – C₀)/(C₁ – C₂) (рис. 4.6).

4.5.4. Диффузия в среде с цилиндрической симметрией

Уравнение (4.14) для радиального потока в цилиндре преобразуется в уравнение Бесселя нулевого порядка. Его решение выражается через соответствующие функции Бесселя, выбор которых зависит от граничных и начальных условий.

Диффузия в цилиндре с постоянной концентрацией на поверхности

Распределение концентрации диффундирующего вещества в цилиндре радиусом r_ц при постоянной концентрации С₁ на поверхности выражается уравнением

,

где:

_n – n-й корень уравнения I₀ (_nr_ц) = 0;

I₀ (x) – функция Бесселя первого рода нулевого порядка;

I₀ (х) – ее дифференциал.

Первые четыре корня уравнения I₀ (_nr_ц) равны

; ; ; . (4.15)

Эти корни дают четыре члена бесконечного ряда, которых достаточно для практических целей. При больших значениях t обычно ограничиваются одним членом функции Бесселя. Данная функция I₀ (x) и ее дифференциал I₀ (х) даются рядами

; (4.16)

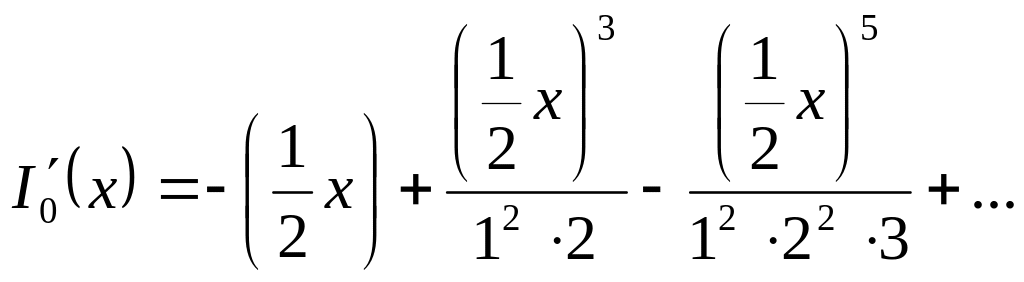(4.17)

Их значения приводятся в специальных таблицах.

Количество вещества m_в, продиффундировавшего через единицу длины цилиндра за время t, определяется выражением

,

где первые четыре значения а рассчитываются по формулам (4.15).

Диффузия в цилиндре с начальным распределением концентраций С = f(r)

Распределение концентрации растворенного вещества в текущий момент времени t при граничных и начальных условиях: С₁ = 0 при r = r_ц для всех t, С = f(r) для r_ц < r < 0 при t = 0 следующее:

.

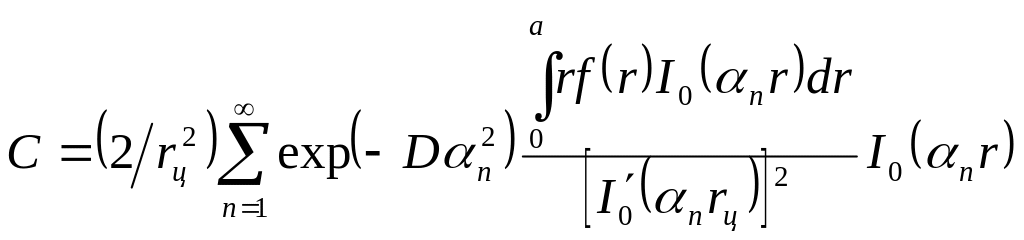При f(r) = С₀

.

Значения _n, I₀(_n, r) и I₀(_nr_ц) находят по соотношениям (4.15) – (4.17).

Количество растворенного вещества, продиффундировавшего из цилиндра через единицу его длины, рассчитывается по формуле

.

Если граничные и начальные условия имеют вид С = С₁ при r = r_ц для всех t, С = f(х) для r_ц < r < 0 и t = 0, распределение концентрации растворенного вещества определяется выражением

.

При f(r) = С₀

.

Рис. 4.7. Зависимость коэффициентов ¹ и ¹ от параметра 

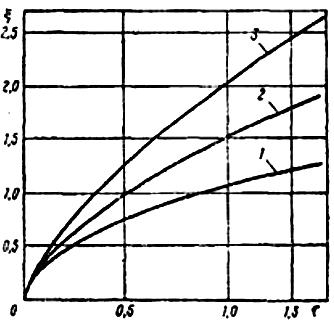
Рис. 4.8. График функции () для случаев растворения в матрице плоского (1),

цилиндрического (2) и сферического (3) включений