4.5.2. Диффузия через плоскую поверхность Диффузия из бесконечно тонкого слоя в неограниченный образец

Неограниченный образец считается бесконечной средой (∞ < х < ∞). В точке х₀ находится бесконечно тонкий слой диффундирующего вещества (мгновенный источник мощностью Q_и). Во всех других точках образца в начальный момент концентрация этого вещества равна 0. В момент времени t распределение концентрации диффундирующего вещества описывается выражением:

.

В частном случае при х₀ = 0

.

Максимального значения в этом случае концентрация достигает при х = 0. Распределение вещества, имеющее в начальный момент характер функции, со временем изменятся, как показано на рис. 4.3. Максимум кривой распределения соответствует .

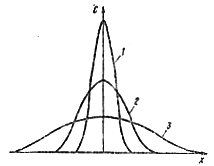
Рис. 4.3. Концентрационные кривые диффузии из бесконечно тонкого слоя в неограниченный образец: 1 – при t₁; 2 – при t₂; 3 – при t₃ (t₃ > t₂ > t₁)

Диффузия из слоя конечной толщины 2ас в неограниченный образец

При t = 0 в слое конечной толщины – а_с < х < а_с концентрация диффундирующего вещества постоянна и равна С₀, а в остальных точках С(х,0) = 0. При этих условиях

,

где:

erf z – функция ошибок Гаусса (или иначе интеграл вероятности) определяется по формуле

.

Значения функции ошибок, ее производных и интегралов табулированы (табл. 4.3). Графики распределения концентраций при диффузии из слоя конечной толщины для различных значений , приведены на рис. 4.4.

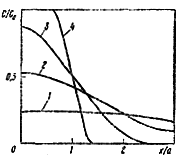
Рис. 4.4. Концентрационные кривые диффузии из слоя конечной толщины в неограниченный образец: 1 – ; 2 – ; 3 – ; 4 –

Диффузия в полуограниченный образец

При диффузии в полуограниченный образец (0 < х < ) с нулевой начальной концентрацией С (х, 0) = 0 из другого полуограниченного образца (–  < х< 0) с постоянной начальной концентрацией С₀ концентрация диффундирующего вещества изменяется в соответствии с выражением

и распределение концентраций при различных значениях t имеет вид, изображенный на рис. 4.5.

При t > 0 концентрация в плоскости раздела (плоскость х = 0) постоянна и равна С₀/2. Если на плоской поверхности (х = 0) поддерживается постоянная концентрация С₀, не зависящая от времени, то

.

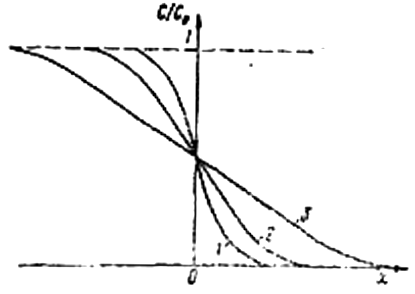
Рис. 4.5. Концентрационные кривые диффузии из одного полуограниченного образца в другой: 1 – при t₁; 2 – при t₂; 3 – при t₃ (t₃ > t₂ > t₁)

Таблица 4.3

Функция ошибок Гаусса, ее производные и интегралы

	exp(z2) erfc (z)	– ½ 4z exp(– z2)	– ½ 2 exp(– z2)	erf z	erfc (z)	2 erfc (z)	42 erfc (z)
0 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 0,6 0,7 0,8 0,9 1,0 1,2 1,4 1,6 1,8 2,0 2,5 3,0	1,0 0,9460 0,8965 0,8509 0,8090 0,7703 0,7346 0,7015 0,6708 0,6423 0,6157 0,5678 0,5259 0,4891 0,4565 0,4276 0,3785 0,3387 0,3060 0,2786 0,2554 0,2108 0,1790	0 0,1126 0,2234 0,3310 0,4336 0,5300 0,6188 0,6988 0,7692 0,8294 0,8788 0,9447 0,9678 0,9520 0,9035 0,8302 0,6416 0,4450 0,2791 0,1591 0,0827 0,0109 0,0008	1,1284 1,1256 1,1172 1,1033 1,0841 1,0600 1,0313 0,9983 0,9615 0,9215 0,8788 0,7872 0,6913 0,5950 0,5020 0,4151 0,2673 0,1589 0,0872 0,0442 0,0207 0,0022 0,0001	0 0,05637 0,11246 0,16800 0,22270 0,27633 0,32863 0,37938 0,42839 0,47548 0,52050 0,60386 0,67780 0,74210 0,79691 0,84270 0,91031 0,95228 0,97635 0,98909 0,99532 0,99959 0,99998	1,0 0,9436 0,88754 0,83200 0,77730 0,72367 0,67137 0,62062 0,57161 0,52452 0,47950 0,39614 0,32220 0,25790 0,20309 0,15730 0,08969 0,04772 0,02365 0,01091 0,00468 0,00041 0,00002	1,1284 1,0312 0,9396 0,8537 0,7732 0,6982 0,6284 0,5639 0,5043 0,4495 0,3993 0,3119 0,2402 0,1823 0,1364 0,1005 0,0521 0,0253 0,0115 0,0049 0,0020 0,0001 –	1,0 0,8921 0,7936 0,7040 0,6227 0,5491 0,4828 0,4233 0,3699 0,3223 0,2799 0,2090 0,1541 0,1120 0,0803 0,0568 0,0272 0,0122 0,0052 0,0021 0,0008 – –
П р и м е ч а н и е. Выражением erfc (z) обозначена разность 1 – erf z.