4.4. Типы связей между компонентами

В КМ связи между матрицей и волокнами могут быть шести типов. Механическая связь (рис. 4.2, а) осуществляется за счет чисто механического зацепления неровностей контактирующих поверхностей матрицы m и волокна f или за счет сил трения. КМ с этим типом связи имеют низкую прочность при поперечном растяжении и продольном сжатии.

Связь при смачивании и растворении (рис. 4.2, б) реализуется благодаря силам поверхностного натяжения. Обычно смачивание сопровождается небольшим растворением компонентов. Этот тип связи реализуется при пропитке волокон f расплавленной матрицей m в отсутствие химических реакций. Как и предыдущий, он характерен для КМ первого класса.

Реакционная связь (рис. 4.2, в) возникает при протекании химической реакции на границе раздела m и f с образованием новых химических соединений mf_х. Этот тип связи присущ КМ третьего класса.

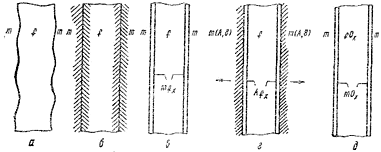
Рис. 4.2. Схемы основных типов связи: а – механическая связь; б – связь путем смачивания и растворения, например Nb-W; в – реакционная связь, например Ti-С; г – обменно-реакционная связь, например Ti (А1)-В; д – оксидная связь

Обменно-реакционная связь (рис. 4.2, г) является разновидностью реакционной связи, когда общая химическая реакция происходит в несколько стадий, одна из которых контролирует скорость образования связи. Например, матрица m из титана А, легированного алюминием В, взаимодействует с борными волокнами f в две стадии. Вначале твердый раствор алюминия в титане реагирует с бором с образованием сложного диборида Аf_х, который затем реагирует с титаном, образуя диборид титана и твердый раствор алюминия в титане.

Оксидная связь (рис. 4.2, д) также может рассматриваться как разновидность реакционной связи, которая характерна для металлов m, армированных волокнами из оксидов fО_х. Эта связь реализуется за счет образования либо шпинелей на межфазных границах, либо продуктов реакции в виде оксидной пленки mО_х, через которую осуществляется связь.

Смешанный тип связи возникает в КМ псевдопервого класса после разрушения оксидных пленок и начала химического или диффузионного взаимодействия. Он реализуется, например, при частичном переходе систем псевдопервого класса в системы второго и третьего классов.

4.5. Процессы диффузии между компонентами км

Анализ межфазного взаимодействия в КМ, компоненты которого образуют между собой твердые растворы или соединения, связан с решением двух типов задач. Первый тип – расчет распределения концентраций компонентов в диффузионной зоне по известному коэффициенту диффузии при заданных граничных и начальных условиях – решается обычно на основе уравнений диффузии Фика, описывающих закономерности переноса вещества. Целью задач второго типа является определение коэффициентов диффузии или констант (коэффициентов) скорости роста диффузионных зон по известному распределению концентраций в этих слоях.

4.5.1. Уравнения Фика

Первый закон Фика. Уравнение первого закона Фика для одномерной диффузии в направлении х записывается в виде:

,

где:

j_x – плотность потока вещества (в направлении х). Знак «минус» означает, что поток направлен из области с большей концентрацией в область с меньшей. Для трехмерной диффузии уравнение первого закона Фика приобретает форму j_x = – D·gradС.

Второй закон Фика. Математически второй закон Фика для одномерной диффузии выражается уравнением:

,

для трехмерной диффузии – уравнением:

(4.10)

или

.

Если коэффициент диффузии D зависит от концентрации С, то

.

Уравнение (4.10) с учетом преобразований x = r·sinθ·cosφ; y = r·sinθ·sinφ; z = r·cosφ в сферических полисных координатах r, θ, φ принимает вид:

. (4.11)

Для диффузии в среде со сферической симметрией уравнение (4.11) переходит в уравнение

, (4.12)

так как и .

С учетом x = r·cosθ и y = r·sinθ уравнение (4.10) выражается в цилиндрических координатах r, θ, z

(4.13)

При малых концевых эффектах принимается и и уравнение (4.13) преобразуется к более простому виду

. (4.14)