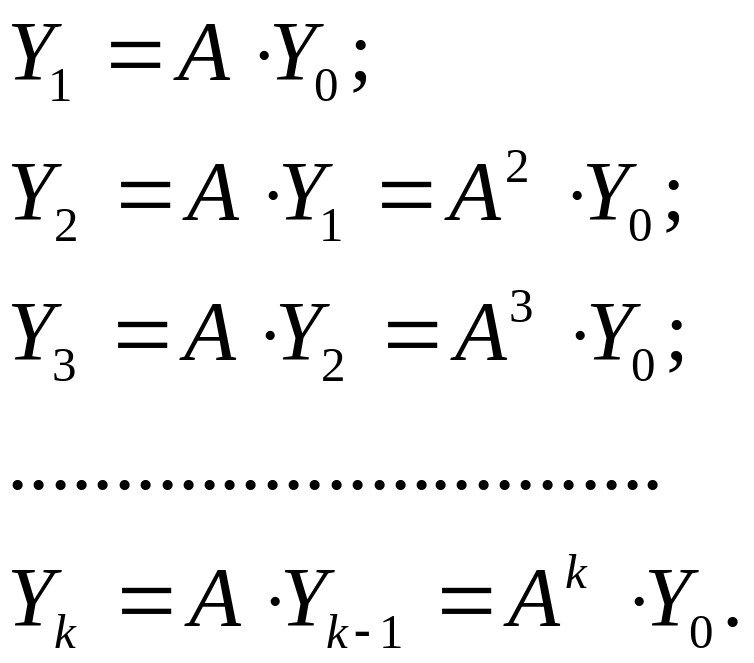2) Расчет рангов частных критериев.

В случае большого числа критериев задача непосредственного определения рангов критериев оказывается весьма трудной и даже неразрешимой для экспертов в силу ограниченности психико-физиологических возможностей человека. При этом при сравнении двух альтернатив эксперт обычно способен адекватно определить, у какой из них рассматриваемый признак выражен сильнее, а также качественно (вербально) оценить, насколько велика разница между наблюдаемыми у двух альтернатив признаками. Для нахождения рангов частных критериев удобнее всего применить известный метод, используемый при решении многокритериальных задач, метод МАИ. [17, с. 53]. Суть метода изложим ниже.

Попарное сравнение всех частных критериев проводится с помощью шкалы лингвистических оценок. Лингвистическая шкала состоит из девяти градаций оценок относительной важности. Такая шкала отражает особенности человека как субъекта принятия решений и обработки информации. Человек плохо воспринимает излишне детализированные шкалы значений признаков. Психофизические данные свидетельствуют о том, что человек уверенно различает не более 72 градаций на шкале некоторого признака (параметра). Если же шкала содержит большее число градаций, то соседние уровни начинают сливаться, и уже не могут быть с уверенностью разграничены. Сделанным лингвистическим суждениям экспертов в соответствии с таб.2.2 присваиваются соответствующие численные оценки от 1 до 9. Через a_ij обозначена оценка значимости критерия i по отношению к критерию j. На основе всех определенных попарных оценок a_ij далее строится матрица парных сравнений А{a_ij}.

Таблица 2.2

Лингвистические оценки относительной важности

Степень важности	Определение	Комментарии
1	2	3
1	Одинаковая значимость	Два действия вносят одинаковый вклад в достижение цели
3	Некоторое преобладаниё значимости одного действия над другим (слабая значимость)	Существуют соображения в пользу предпочтения одного из действий, однако эти соображения достаточно убедительны
5	Существенная или сильная значимость	Имеются надежные данные или логические суждения для того, чтобы показать предпочтительность одного из действий действий
7	Очевидная или очень сильная значимость	Убедительное свидетельство в пользу одного действия перед другим
9	Абсолютная значимость	Свидетельства в пользу предпочтения одного действия другому в высшей степени убедительны
2,4,6,8	Промежуточные значения между двумя соседними суждениями	Ситуация, когда необходимо ком­промиссное решение
Обратные величины приведенных выше ненулевых величин	Если при сравнении объекта A с объектом B мы получим одно из приведенных выше значений, то, соответственно, результат сравнения объекта B с объектом A есть обратная величина.

Источник: [17]

Пусть А - матрица парных сравнений, построенная на основе определенных экспертами значений элементов матрицы а_ij. Через w₁, w₂, ..., w_n обозначим искомые значения весовых коэффициентов критериев. W = (w₁, w₂, ..., w_n ) - вектор приоритетов, отвечающий предпочтениям лиц принимающих решение; n - количество частных критериев.

Вектор приоритетов находится из уравнения (2.5)

,

(2.5)

где - собственное значение матрицы А.

Для нахождения собственного значения воспользуемся приближенными методами. В данной работе мы воспользовались алгоритмом определения наибольшего по модулю собственного значения матрицы при помощи последовательных итераций.

Теорема: Пусть - собственные значения матрицы А порядка n. Допустим, что , где последовательность расположена в порядке убывания, причем остальные , где i>2 могут быть равными. Возьмём произвольный вектор , где . Тогда для нахождения образуем последовательность итераций:

(2.6)

Если k достаточно велико, то максимальное собственное значение матрицы А находим из условия .

Для нахождения вектора приоритетов решаем систему линейных уравнений:

В роли экспертов были взяты два должностных лица из учреждения управления (Гродненский областной исполнительный комитет) и один эксперт из высшего учебного заведения, ведущего подготовку специалистов по экономической квалификации. Суждения экспертов будем считать однородными.

Обозначим – вес j - го показателя i -ой компоненты «качество жизни», где , и выполняются условия: .

Через – вес i‑ой компоненты «качество жизни» при этом выполняется: .