2. Дисперсия суммы случайных величин. Корреляционный момент.

Пусть ислучайные величины. Рассмотрим их сумму.

Математическое ожидание этой суммы будет равно сумме математических ожиданий.

Найдем дисперсию суммы случайных величин Вычтем из первого уравнения второе и возведем в квадрат.

Для сокращения записи введем обозначения:

Тогда,

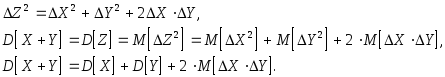
Величину принято обозначатьи называть корреляционным моментом, или моментом связи случайных величини. Тогда дисперсии суммы равна сумме дисперсий плюс удвоенный корреляционный момент.

Основное свойство корреляционного момента.

Если величины инезависимы, то их корреляционный момент равен нулю.

Обратное утверждение неверно.

3. Теорема сложения дисперсий.

Из последнего свойства следует, что если величины и независимы, то дисперсия их суммы рав­на сумме их дисперсий.

.

Этой теоремой широко пользуются в теории погрешностей при обработке результатов косвенных измерений, так как входящие в расчетные формулы величины в большинстве случаев являются независимыми, и поэтому подсчитывая среднеквадратичную погрешность вы суммируете квадраты всех погрешностей.

4. Коэффициент корреляции.

Полученный выше корреляционный момент зависит от выбора единиц измерения и .Это за­труд­няет сравнение корреляционных моментов различных случайных величин. Поэтому удобнее поль­зоваться безразмерной величинойкоэффициентом корреляции:

где среднеквадратичные отклонения случайных величин и .

Без доказательства дадим следующие свойства коэффициента корреляции:

1. Коэффициент корреляции ;

2. Если близко к 1, зависимость между и близка к линейной; если, то корреляция положительна, еслиотрицательная.

3. Когда , величины и связаны функциональной линейной зависимостью.

5. Оценка значимости коэффициента корреляции.

При проведении корреляционного анализа часто возникает вопрос, являются ли полученные из на­блю­дений коэффициенты значимыми и не объясняется ли их появление случайным характером вы­борки.

Фактически, полученный коэффициент корреляции всегда является выборочным, так как он вы­чис­ляется на основе ограниченной совокупности, представляющей выборку из генеральной. Поэтому он имеет ошибку выборочности, которая является мерой расхождения между и коэффициентом корреляции для генеральной совокупности. Определив среднюю ошибку, мож­но судить о степени достоверности.

Принимается нулевая гипотеза, согласно которой , то есть считается, что в генеральной со­во­купности нет корреляции между варьирующими признаками. Тогда критерий Стьюдента рас­счи­ты­вается по формуле:

Если выборка достаточно велика , то

Т.к. распределение при малыхвыборках может значительно отличаться от нор­маль­но­го, для расчета критерия Стьюдента пользуются формулой:

Если найденное значение превышает табличное для заданного уровня значимости и числа степеней свободы, можно считать нулевую гипотезу отвергнутой, т.е. признать данное значениедостоверным. Если же, то нулевая гипотеза принимается и найденный коэффициент корреляции нельзя считать достоверным, т.е. корреляции между варьирующими признаками нет.

7. Измерение связи. Регрессия.

   1. Понятие о регрессии. Уравнение регрессии.

Коэффициент корреляции указывает лишь на степень связи в вариации двух переменных ве­личин, но не дает возможности судить о том, как количественно меняется одна величина по мере изменения другой. На этот вопрос отвечает метод регрессии. Регрессия может быть двусторонней: определение изменения по изменению, и определение измененияпо изменению. Эмпирическая линия регрессии обычно представляет собой ломаную линию. Если в силу каких-либо причин мы можем предположить, что исследуемая зависимость является линейной, то мы можем заменить ломаную линию прямой. Уравнение прямой линии имеет вид: Задача состоит в определении коэффициентов регрессииВ общем случае они определяют наклон прямой линии и пересечение с осью У.

Для двусторонней регрессии следует различать

Коэффициент можно найти по известным значениям