Теплоемкость тела

.

Теплоемкость при постоянном объеме

.

Теплоемкость при постоянном давлении

.

Здесь введена новая термодинамическая величина , называемая энтальпией

.

В тепловых процессах при постоянном давлении . Поэтому ее еще называют тепловой функцией. Энтальпия так же как и внутренняя энергия является однозначной функцией состояния термодинамической системы.

Из первого начала термодинамики следует, что всегда . Рассмотрим значения этих величин для идеального газа. В этом случае внутренняя энергия равна полной кинетической энергии теплового движения молекул. Тогда для одного моля идеального газа

.

Отсюда получаем выражения для молярных теплоемкостей

, , .

Последнее соотношение называется уравнением Майера. Оно справедливо только в случае идеального газа. В дальнейшем нам понадобится еще одна важная величина

,

называемая показателем адиабаты. Для идеального газа она, очевидно, равна

.

66666666666666666666666666666666666

. Адиабатический процесс ( ).

Тепловой процесс с телом, в котором оно не обменивается теплом с другими телами, назы-вается адиабатическим. Из первого начала термодинамики следует, что в таком процессе . Для идеального газа , поэтому при адиабатическом расширении идеаль-ный газ охлаждается, а при адиабатическом сжатии – нагревается.

Для одного моля идеального газа

, или .

Производя интегрирование, получаем

, .

Возводя последнее выражение в степень и используя уравнение Майера, приходим к уравнению

.

Это так называемое уравнение Пуассона для адиабатического процесса в идеальном газе. С помощью уравнения Клапейрона - Менделеева его можно представить в следующих формах

, или .

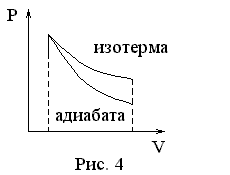
Из уравнения Пуассона видно, что если из одного и того же начального состояния с идеальным газом производится либо изотермический процесс (изотерма на рис. 4), либо адиабатический процесс (адиабата), то адиабата лежит ниже изотермы.

Типичным примером адиабатического процесса в идеальном газе является звуковая волна, которую мы рассмотрели в курсе механики. В этом случае успевает установиться локальное равновесие, но перенос тепла между областями с разным давление произойти не успевает.

Все рассмотренные выше процессы происходят при постоянной теплоемкости. Можно ввести еще один тип процессов в идеальном газе.

5. Политропический процесс ( ).

Аналогично случаю адиабатического процесса с помощью первого начала термодинамики для такого процесса можно получить уравнение политропы

, где - показатель политропы.

Для адиабатического процесса , , для изотермического - , , для изохорического - , , для изобарического - , .

7777777777777777777777777 Идеальный газ во внешнем поле.

Р

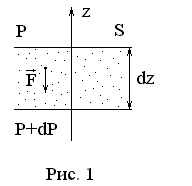
ассмотрим малый элемент объема идеального газа, заключенный между двумя площадками , перпенди-кулярными потенциальной внешней силе и отстоя-щими друг от друга на расстоянии (рис. 1). Ось направлена противоположно силе . Давления газа на верхней и нижней площадках равны соответственно и . Тогда условие равновесия выделенного объема можно представить в виде

, или ,

где - потенциальная энергия молекулы газа. Будем считать, что температура газа постоянна во всем объеме. Из уравнения Клапейрона (локальное равновесие) получим

, .

Интегрируя это уравнение, получаем формулу Больцмана для распределения молекул идеального газа по координатам во внешнем потенциальном поле

.

Здесь - концентрация молекул газа в точке , в которой . Аналогично для давления

. В поле тяжести .

Последнее выражение носит название барометрической формулы. На ней основано устрой-ство альтиметра – прибора для определения высоты над поверхностью Земли.

*88888888888888888888888888888888888888888888888

2. Распределение молекул по скоростям.

Мы уже ввели понятие средней квадратичной скорости молекул . Но молекулы в газе движутся с разными скоростями и важно определить какая часть молекул имеет скорости в определенном интервале значений. Рассмотрим интервал значений проекции скорости между и . Число молекул в единице объема с такими значениями можно представить в виде

. (1)

Функция в этом выражении называется функцией распределения по проекции скорости .

Вероятностный смысл можно пояснить, если переписать выражение (1) по другому

.

Таким образом, вероятность того, что проекция скорости молекул лежит в интервале от до равна .

Теорема сложения вероятностей.

Если - вероятности исключающих друг друга событий, то вероятность того, что осуществится какое-нибудь одно из них

.

Имеет место также теорема для вероятности независимых событий. Например, бросание монеты и следующая за этим попытка сдать экзамен.

Теорема умножения вероятностей.

Вероятность совмещения нескольких независимых событий равна произведению вероят-ностей каждого из них в отдельности

.

Решая это дифференциальное уравнение, находим

. (3)

Для функции распределения выполняется условие нормировки

,

означающее, что попадание в интервал от до является достоверным событием. Подставляя в это условие выражение (3), находим константу

.

Константу можно найти с помощью равенства

.

Проводя интегрирование, находим . Подставляя и в выражение (3), получаем распределение Максвелла по проекции скорости молекул на ось

.

1111111111111111111111111111 11111111111111111111111111111111.

Броуновское движение.

Одним из убедительных доказательств молекулярно-кинетической теории является так называемое броуновское движение, открытое в 1827 г. английским ботаником Броуном.

Он обнаружил, что при рассмотрении под микроскопом частицы, взвешенные в жидкости, находятся в непрерывном беспорядочном движении. Оно возникает вследствие ударов со стороны движущихся молекул жидкости. На основе такого представления Эйнштейном и Смолуховским была построена теория броуновского движения (1906 г.). Ее основные положения состоят в следующем. Движение крупной (по сравнению с размером молекул) частицы массы в жидкости можно описать в проекции на ось с помощью уравнения

, (1)

где первое слагаемое в правой части представляет собой силу вязкого трения по формуле Стокса, а есть сила случайных толчков со стороны молекул жидкости. Назовем подвижностью частицы величину . После несложных преобразований можно привести уравнение (1) к следующему виду

. (2)

Усредним уравнение (2) по всем броуновским частицам. В силу хаотичности движения молекул . Так как броуновские частицы находятся в тепловом равновесии с моле-кулами жидкости, то . При таких предположениях после усреднения получим

.

Решение этого уравнения имеет вид и называется формулой Эйнштейна. Она была экспериментально подтверждена в опытах Перрена в 1908 г.

12121212121212121212

12121212121212121212

12121212121212121212

С помощью (2) можно получить выражение для длины свободного пробега . Очевидно,

.

При получении (1) мы считали молекулы внутри выделенного цилиндра неподвижными. Можно уточнить выражение для , если учесть относительное движение молекул. Легко показать, что средняя скорость относительного движения . Отсюда

. (3)

Эффективное сечение столкновений.

Е

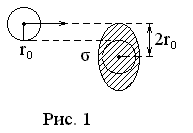
сли молекула с радиусом налетает на другую такую же молекулу, то они столкнутся, если расстояние между их центрами не превышает (рис. 1). Площадь заштрихованной окружности называется эффективным сечением столкновений.

Если центр налетающей молекулы попадает в заштрихованную площадку (прицельная площадь) , то молекулы сталкиваются. Эффективное сечение столкновений имеет также вероятностный смысл. Можно показать, что величина численно равна вероятности столкновения молекулы в единице объема.

131313131313131313131313

131313131313131313131331

131313131313131313131313

Переход от неравновесных состояний к равновесным происходит благодаря явлениям переноса. При этом происходит выравнивание значений термодинамических параметров. В зависимости от вида переносимых физических величин можно выделить три явления переноса.