2. Поняття похідної.

2.1 Задачи, яки приводять до поняття похідної.

Задача 1. Швидкість руху.

Нехай вздовж деякої прямої рухається точка за законом , де - шлях, який пройшла точка, - час. Потрібно знайти швидкість точки у момент часу .

У момент часу шлях, який пройшла точка дорівнює .

У момент часу шлях дорівнює . Тоді за проміжок

часу середня швидкість дорівнює . Якщо , то середня швидкість краще характеризує рух точки у момент часу . Тому швидкість

точки у момент часу - це границя середньої швидкості за проміжок часу від до , коли , тобто .

Задача 2. Продуктивність праці.

Нехай кількість виробленої продукції характеризується рівністю

за час . Потрібно знайти продуктивність праці у момент часу .

У момент часу кількість виробленої продукції дорівнює .

У момент часу кількість виробленої продукції дорівнює

. Тоді за проміжок часу середня продуктивність праці

визначається формулою . Якщо , то середня продуктивність праці краще характеризує продуктивність праці у момент часу - це границя середньої продуктивності праці за період часу від до , коли , тобто .

Якщо у розглянутих задачах відволіктися від конкретних величин, то розв`язування кожної з них веде до знаходження границі відношення приросту функції до приросту незалежної змінної, коли останній прямує до нуля. Математики це помітили і ввели абстрактне поняття похідної функції.

0. 2.2 Означення похідної функції.

Розглянемо функцію , яка визначена на деякому проміжку та її графік.

На графіку функції зафіксуємо точку та візьмемо точку .

Аргумент отримало приріст , тобто . Значення функції – приріст , тобто Складемо відношення , яке показує, в скільки разів на проміжку приріст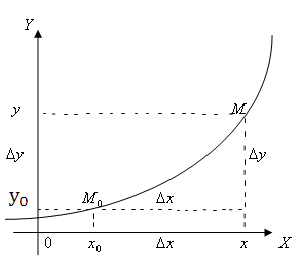

функції більше ніж приріст аргументу , тобто визначає середню швидкість зміни значення функції відносно зміни аргументу .

При і . Тому вираз також прямує до деякої величини, яка визначається виразом та показує швидкість зміни функції у точці .

Якщо , , , , то .

Якщо існує ця границя, то її називають похідної функції у точці і позначають , , , .

Означення.

Границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля, називається похідної функції у точці

.

Означення.

Операція знаходження похідної називається диференціюванням.

Означення.

Функція, яка має похідну у точці, називається диференційованою у цій точці.

За допомогою означення похідної можна знайти похідні елементарних функцій.

Наприклад. За допомогою означення похідної знайдемо похідну

функції у точці .

Таким чином, .

За допомогою означення похідної виведена таблиця похідних елементарних функцій та правила диференціювання.