12. Определенный. Интеграл Римана; разбиение сегмента, измельчение, объединение, диаметр разбиений. Интегральные суммы.

Введем понятие разбиения отрезка [a,b] измельчением этого разбиения и объединения 2-х разбиений. Опр1. Будем говорить, что задано разбиение [a,b], если заданы (.) x₀,x₁,...,x_n: a=x₀<x₁<...<x_n=b. Разбиение [a,b] будем обозначать {x_k}_(k=0,k=n) или {x_k}. Опр2. Разбиение {x_k} [a,b] называется измельчением разбиения {x_k} того же сегмента, если каждая (.) x_p разбиения {x_k} совпадает с одной из (.) x_q разбиения {x_k}. Опр3. Разбиение {x_k} [a,b] называется объединением разбиений {x_k} и {x_k} того же сегмента, если все (.) разбиений {x_k} и {x_k} являются (.) разбиения {x_k} и других (.) разбиение {x_k} не содержит. Пусть на [a,b] задана функция f(x) и пусть {x_k} - некоторое разбиение [a,b]; выберем на каждом из отрезков [x_k-1,x_k], k=1,...,n произвольным образом (.) _k, k=1,...,n и составим сумму Sn= 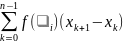(1), _k[x_k+1,x_k], k=0,…,n-1; число Sn (1) называется интегральной суммой для функции f(x). Интегральная сумма Sn зависит как от разбиения {x_k}, так и от выбора (.) _k на [x_k+1,x_k]. Если ввести обозначение x_k=x_k+1-x_k, k=0,...,n-1, то интегральную сумму можно записать в виде: Sn=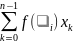 (2), _k[x_k+1,x_k].

Сегменты [x_k+1,x_k] принято называть частичными, а (.) _k - промежуточными (.). Число d=max_1kn x_k=max_k x_k-диаметр или мелкость разбиения x_k.Опр4. число I называется пределом интегральной суммы Sn при стремлении {x_k} к 0, если для  >0  >0: d>  _k I-<. Обозначение I=lim_d0 Sn=lim_d0 Sn. Опр5. Функция f(x) называется интегральной по Риману на [a,b], если для этой функции на указанном сегменте  конечный предел I ее интегральных сумм Sn при стремлении диаметра d разбиений {x_k} к 0. Число I-определенный интеграл Римана от функции f(x) в пределах от a до b (или по [a,b]) ∫_(a,b) f(x)dx=lim_d0 Sn. Переменную x можно заменить на любую другую. Это было по Коши. Теперь на языке последовательностей. Пусть [a,b] последовательно разбивается на части; сначала 1-м способом, потом другим, 3-им и т. д. Последовательность разбиений сегмента на части будем называть основной, если соответствующая последовательность значений диаметров d₁,d₂,... сходится к 0. Равенство I=lim_d0 Sn следует теперь понимать в том смысле, что последовательность значений суммы Sn, отвеч-ая  основной. последовательности разбиения промежутка, всегда  к пределу I как бы при этом не выбирать (.) _k.

13. Ограниченность интегрируемой функции. Неинтегрируемость функции Дирихле.

Геометрический смысл сумм Sn: рисуем на координатной плоскости x0y фигуру, отр-м [a,b] ось 0x отр-ами верт-ых кривых x=a, x=b и гр-ком неотр. непр-ой функции f(x); такая фигура называется кривой трапецией. Если f(x) не является ограниченной на [a,b], то она не интегрируемая по этому отрезку. Покажем, что если f(x) не огр. на [a,b], то для любого разбиения {x_k} этого сегмента значение интегральной суммы Sn можно сделать как угодно большой по абсолютной величине за счет выбора промежуточных (.) ξ_k. Пусть f(x) не ограничена на [a,b]. Фиксируем произвольное разбиение {x_k} [a,b] и произвольное число M>0, т. к. f(x) не ограничена на [a,b], то она не ограничена по крайней мере на одном частичном сегменте, пусть это [x₀,x₁], выберем на каждом из сегментов [x₁,x₂],...,[x_n-1,x_n] (.) ξ_k, kє[x_k-1,x_k], k=2,...,n и зафиксируем. Пусть S₁=f(ξ₂)Δx₁+...+f(ξ_n)Δx_n, выберем ξ ₁є[x₀,x₁]: f(ξ₁)>(S₁+M)/Δx₁, тогда Sn=f(ξ₁)Δx₁+S₁ f(ξ₁)Δx₁-S₁>S₁+M-S₁=M. Предположим теперь, что f(x) интегрируема на [a,b], т. е.  I=lim_d0 Sn.

Фиксируем произв. >0 и выберем >0:  {x_k} [a,b] с диаметром разбиения d< при  выборе промеж. (.) _k выполняется неравенство: I-<, т. е. I-<<+I (3). Из (3)  что  c>0: для  {x_k} [a,b] с диаметром d< при  выборе промеж. (.) _k выполняется неравенство: <c. Однако, в силу уже доказанного, для  {x_k} [a,b] с диаметром d< при  выборе промежутка (.) _k можно выбрать так, что будет выполняться >c, т. о. получим противоречие  f(x) не интегрируется на [a,b]. Покажем теперь, что не всякая ограниченная функция интегрируется на примере функции Дирихле: _Q(x)={1, xQ; 0, xQ}. Рассмотрим эту функцию на отрезке [0, 1]. Она, очевидно, ограничена на нем. Покажем, что она не интегрируема. Зафиксируем произвольное разбиение {X_i}(i=0..i=k) отрезка [0, 1]. Если выбрать точки ξ_i є [х_i-1,x_i], i = 1, 2, ... k, рациональными, то получим Sn=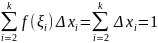 а если взять 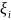иррациональными, то Sn= 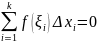. Это верно для любого разбиения {x_i}, следовательно, интегральные суммы Sn заведомо не стремятся ни к какому пределу при |n| -> 0.