
Численное решение уравнения теплопроводности в пакете математических расчетов MathCad
Ввожу исходные данные и вычисляю значения температуры на нулевом временном слое по начальным условиям. Далее задаю матрицу коэффициентов системы - матрицу А и столбец свободных членов (см. рис. 12). Находим решение системы, т.е. температуру на первом временном слое u1, и показываем результат вычислений (см. рис. 13).
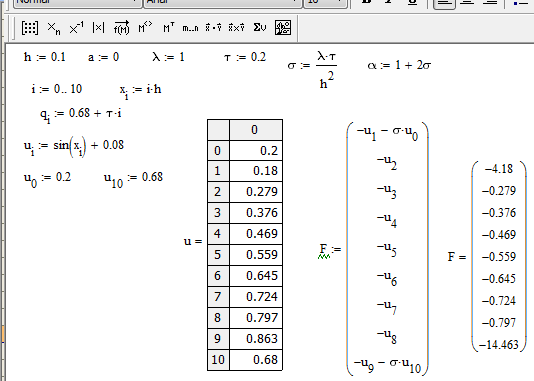
Рис. 12. Подготовка данных для решения уравнения теплопроводности на первом временном слое

Рис. 13. Решение уравнения теплопроводности на первом временном слое
Для получения решения на втором временном слое пересчитываю свободный столбец системы и снова ее решаю (см. рис. 14).

Рис. 14. Решение уравнения теплопроводности на втором временном слое
Повторяя вычисления столбца свободных членов и решения системы еще десять раз, получаю вектора u1, u2, u3…u11, содержащие значения температуры во внутренних точках сетки.
Далее собираю в одну матрицу начальные значения, краевые и вычисленные во внутренних узлах. Формирую нулевую и десятую строки из заданных граничных условий; нулевой столбец матрицы формирую как начальное условие (см. рис. 15);

Рис. 15. Формирование матрицы с результатом
Вывожу результат расчета как единый массив М (см. рис. 16).
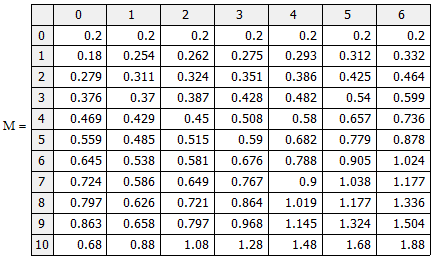
Рис. 16. Результат решения уравнения теплопроводности
Представляю решение графически (см. рис. 17).
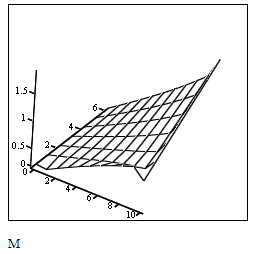
Рис. 17. Графическое преставление решения
Анализ результатов расчета
Решение, полученное средствами обоих пакетов, совпадает с небольшой погрешностью, что подтверждает правильность выполненных расчетов и объясняется различными методами произведения вычислений в представленных программных продуктах. Температура изменяется в области получения решения монотонно, без разрывов.
Получаю максимальное и минимальное значения температуры в рассмотренной области (см. рис. 18), строю графики изменения температуры в точке области х=0,7 и при значении времени t=1 (см. рис. 19, 20).
![]()
![]()
Рис. 18. Анализ решения на максимальное и минимальное значения
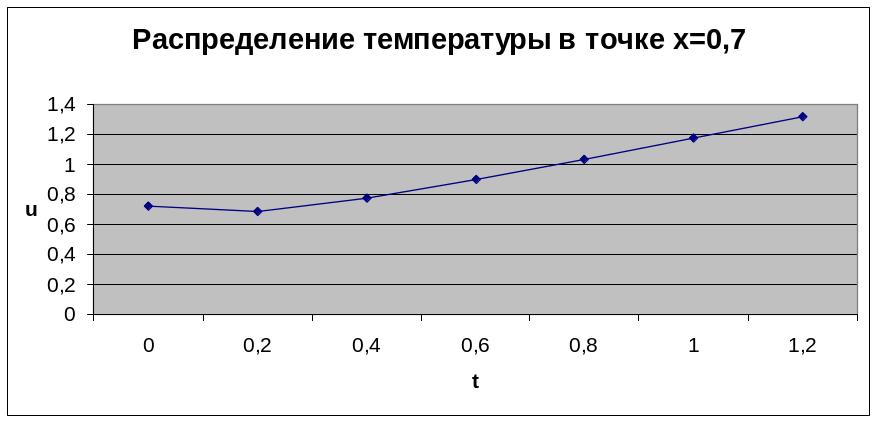
Рис. 19. График изменения температуры в точке области х=0,7
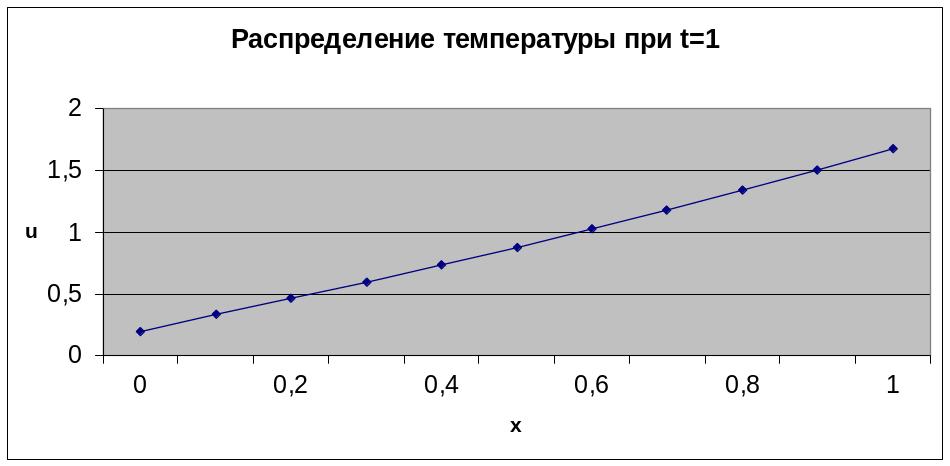
Рис. 20. График изменения температуры в момент времени t=1
Заключение
В результате курсовой работы я развил и закрепил свои навыки работы с табличным процессором Microsoft Excel и применил их для самостоятельного решения с помощью компьютера задачи по нахождению решения уравнения теплопроводности. Решение задачи я подтвердил, проведя расчет с использованием среды программирования MathCAD, изучавшейся в курсе предмета «Программные продукты в математическом моделировании»; результаты совпали.
Библиографический список
Правила оформления курсовых и квалификационных работ. Методические указания /Сост. И.О.Онушкина, П.Г. Талалай .- СПб.: СПГГИ, 2005.-64 с.
Программные продукты в математических моделях. Методические указания к выполнению курсовой работы. / Национальный минерально-сырьевой университет «Горный»; Сост.: О.Г. Быкова. СПб, 2012.-39 с.
