4. Центр паралельних сил. Центр ваги тіла.

4.1 Рівнодіюча систем двох паралельних сил, які не утворюють пару

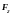
Розглянемо систему двох паралельних сил і , напрямлених в одну (рис.1.7а) чи в протилежні (рис.1.7б) сторони.

Рисунок1.7 – Система двох паралельних сил

Доведемо, що така система сил зводиться до рівнодіючої, яка прикладена в певній точці С. Положення цієї точки для кожного із зазначених випадків знайдемо, обчисливши відносно неї момент рівнодіючої: . Згідно з теоремою Варіньона отримаємо:

,

звідки:

або .

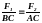Точка С, через яку проходить лінія дії рівнодіючої, називається центром паралельних сил.

Зі співвідношення і рис.1.7 виходить, що лінія дії рівнодіючої двох паралельних, нерівних між собою сил поділяє відстань між точками прикладання цих сил на частини, обернено пропорційні модулям сил – внутрішньо – для сил одного напряму і зовнішньо – для сил з протилежними напрямами.

4.2 Центр паралельних сил

Розглянемо паралельні нерівні між собою сили і в системі координат Oxyz, де точки прикладання цих сил А і В визначаються радіусами-векторами і відповідно. Радіус-вектор визначає точку С прикладання рівнодіючої даних сил (рис.1.8).

Можна записати, що .

Але 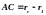і .

Отже:

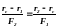, звідки: .

Якщо узагальнити отриманий результат на систему паралельних сил , то отримаємо, що:

.

Рівняння визначає положення центра паралельних сил у векторній формі.

Координати центра паралельних сил обчислюють через проекції радіуса-вектора на осі координат:

; ; .

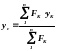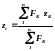Рисунок1.8 – Паралельні нерівні між собою сили

4.3 Центр ваги твердого тіла

Центром ваги тіла називають центр системи паралельних сил, яку наближено утворюють сили ваги його елементарних частинок.

Радіус-вектор центра ваги підраховують як радіус-вектор центра паралельних сил (рис.1.9) за формулою:

,

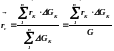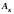де: - радіус-вектор точки прикладання сили ваги елементарної частинки ;

- вага елементарної частинки;

- вага всього тіла.

В граничному випадку, коли число елементарних частинок n прямує до нескінченості, формула (1.35) набуває вигляду:

.

У свою чергу і тому:

,

де: - густина речовини тіла; - елементарний об’єм частинки тіла; - радіус-векор елементарної частинки.

Рисунок 1.9 – Радіус-вектор центра паралельних сил

Координати центра ваги тіла визначаються рівняннями:

, , .

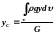Якщо тіло є однорідним, то і 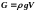. В такому випадку

, , ,

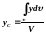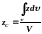де, - об’єм тіла.

Узагальнення результатів визначення центрів ваги однорідних тіл приводить до висновку: якщо однорідне тіло має площину, вісь або центр симетрії, то центр його ваги розташований відповідно або в площині симетрії, або на осі симетрії, або в центрі симетрії.

Методика визначення центра ваги тіл полягає в наступному. Тіло розбивають на скінчену кількість таких частин, для кожної з котрих положення центра ваги відоме, або може бути попередньо визначено. Далі центр ваги підраховують за загальними формулами. Так, наприклад, координати центра ваги плоскої однорідної фігури визначаються з рівнянь:

; ,

у котрих - кількість простих фігур (коло, прямокутник, трикутник), на які розбита задана фігура;

- площа всієї фігури;

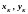- координати центра ваги -ї простої фігури площею .
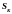
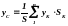