3. Момент сили.

Одним з основних понять теоретичної механіки є поняття моменту сили. З досвіду своєї багатовікової практичної діяльності людина виявила, що під дією сили фізичне тіло може здійснювати не тільки поступальний, але і обертальний рухи.

Міру механічної дії сили на тіло, яка викликає обертальний ефект, називають моментом сили.

Вперше поняття моменту сили ввів у механіку Леонардо да Вінчі. Проте, ще задовго до нього Архімед при розв’язанні задачі про рівновагу важеля інтуїтивно користувався цим поняттям.

Векторний момент сили відносно просторового центра (точки) називається вектор, прикладений в цьому центрі, рівний векторному добутку радіуса-вектора точки прикладання сили на вектор сили.

Згідно з наведеним визначенням векторний момент сили , яка прикладена в точці А відносно центра (рис.1.6), визначається рівнянням :

.

Рисунок 1.6 - Векторний момент сили відносно просторового центра

Модуль вектор-момента, як модуль векторного добутку двох векторів, знаходять за формулою:

.

Перпендикуляр h, який опущений з центра О (рис.1.6) на лінію дії сили , називають плечем сили відносно центра О. Очевидно, що:

.

Тоді:

.

Тобто, числове значення вектор-момента дорівнює добутку сили на плече сили відносно обраного центра. Напрямлений векторний момент сили перпендикулярно до площини, яка проходить через лінію дії сили і моментний центр О, таким чином, що з його кінця можна бачити прагнення сили обертати тіло (площину ОАВ) проти руху годинникової стрілки.

Якщо початок прямокутної декартової системи координат сполучити з центром О (рис.1.6), то для визначення вектор-момента сили користуються також такими формулами:

і

,

де: - орти обраної системи координат;

х,у,z – проекції радіуса-вектора на координатні осі (координати точки А прикладання сили );

- проекції вектора сили на ті ж осі;

- проекції вектор-момента сили на осі координат.

Модуль векторного моменту 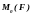і його напрям у просторі при відомих проекціях визначають за формулами:

;

Вектор-момент сили відносно просторового центра має такі властивості:

1. Момент сили відносно центра не змінюється при переносі точки прикладання сили вздовж лінії її дії;

2. Момент сили відносно центра дорівнює нулю, коли лінія дії сили проходить через цей центр;

3. Момент сили відносно центра є зв’язаним вектором.

Моментом сили відносно осі називають алгебраїчну величину, яка дорівнює добутку модуля проекції цієї сили на площину, перпендикулярну до осі, на найкоротшу відстань між точкою перетину осі з площиною і лінією дії проекції сили.

Так, момент сили, наприклад, відносно осі Oz (рис.1.6) за визначенням відповідає формулі:

,

де, - проекція сили на площину Oxy, величина векторна;

- плече сили відносно точки О, тобто перпендикуляр, опущений з точки перетину осі з площиною , на лінію дії проекції .

Момент сили відносно осі вважається додатним, якщо проекція сили на площину, перпендикулярну осі, прагне обертати тіло зі сторони додатного напряму осі проти руху годинникової стрілки, і від’ємним – коли сила намагається обертати тіло за рухом годинникової стрілки.

З визначення моменту можна отримати такі важливі висновки.

1. Момент сили відносно певної осі не змінюється як при переносі точки прикладання сили паралельно обраній осі, так і при переносі центра моментів вздовж цієї осі.

2. Момент сили відносно осі дорівнює нулю, якщо лінія дії сили паралельна осі (в такому випадку дорівнює нулю проекція сили на площину, перпендикулярну осі).

3. Момент сили відносно осі дорівнює нулю, коли лінія дії сили перетинає цю вісь.

Оскільки момент сили відносно осі не залежить від вибору точки на осі, то у подальшому замість позначень будемо використовувати позначення або .