Московский государственный институт электронной техники (Технический Университет).

А.Г.Фокин

Теоретическая механика и теория поля

(конспект лекций для ЭКТ-2)

2008г.

§1. Обобщённые координаты. Понятие числа степеней свободы. 4

§2. Описание эволюции системы в конфигурационном пространстве (КП). 5

§3. Принцип Гамильтона (наименьшего действия). 6

§4. Функция Лагранжа и её свойства. 7

§5. Правило суммирования Эйнштейна. 7

§6. Функция Лагранжа простейших систем. 8

§7. Интегралы движения в методе Лагранжа. 11

§8. Преобразование Галилея. 11

§9. Свойства симметрии пространства и времени. 11

§10. С и l системы. 13

§11. Циклические координаты. 14

§12. Задача двух тел и сведение её к эквивалентной одномерной. 14

§13. Особенности движения частицы в центральном поле. 16

§14. Одномерный эффективный потенциал. 17

§15. Обобщенный импульс. Преобразование Лежандра. Уравнения Гамильтона. 17

§16. Фазовое пространство. 19

§17. Функция Гамильтона и её свойства. 19

§18. Функция Гамильтона простейших систем. 19

§19. Интегралы движения в методе Гамильтона. 21

§20. Скобки Пуассона и их свойства. 21

§21. Малые колебания и свойства потенциальной энергии. 25

§22. Колебания с одной степенью свободы. Характеристическое уравнение. 25

§23. Колебания с n степенями свободы. 28

§24. Затухающие одномерные колебания. 34

§25. Элементы тензорного анализа в классической механике. 35

§26. Оператор . 37

§27. Уравнения Максвелла для электромагнитного поля в вакууме. 38

§28. Потенциалы электромагнитного поля в вакууме. 38

§29. Градиентная инвариантность. 39

§30. -функция. 39

§31. Объёмная плотность точечного заряда. 40

§32. Закон сохранения заряда. 41

§33. Типы калибровок. 41

§34. Уравнения Максвелла в среде без учёта пространственно-временной дисперсии. 44

§35. Теорема Стокса. 45

§36. Функциональные соотношения различных полей 46

§37. Тензоры и их свойства. 48

§38. Условия на границе раздела двух сред. 48

§39. Уравнения Максвелла для стационарного электромагнитного поля в среде. 51

§40. Приближение линейного тока 53

§41. Уравнения Максвелла для квазистационарного электромагнитного поля. 55

§42. Условия квазистационарности поля. 56

§43. Глубина проникновения квазистационарного электромагнитного поля. 57

§44. Функция Грина уравнения Гельмгольца. 58

§45. Уравнения Максвелла электромагнитных волн в вакууме. 59

§46. Волновое уравнение в случае вакуума. 60

§47. Решение волнового уравнения в случае плоской электромагнитной волны в вакууме. 60

§48. Плоская монохроматическая волна. 62

§49. Уравнения Максвелла в случае плоской монохроматической волны в вакууме. 62

§50. Разложение электромагнитных полей по плоским монохроматическим волнам. 63

§51. Калибровка Лоренца в случае однородной изотропной среды. 63

Задачи по курсу «Теоретическая механика и теория поля» 64

Задачи по курсу «Теоретическая механика и теория поля» и их решение. 69

Экзаменационные вопросы по курсу «Теоретическая механика и теория поля». 75

Задачи по курсу «Теоретическая механика и теория поля» и их решение (от А.Е.Широкова) 77

§1. Обобщённые координаты. Понятие числа степеней свободы.

Пусть число степеней свободы равно . Для задания пространственного положения системы необходимы координаты.

– размерность пространства.

– число материальных точек.

числу координат, с помощью которых можно задать положение материальных точек.

– радиус вектор а-той точки.

Если имеются связи, т.е. ограничения, накладываемые на движение системы, причём выраженные в форме уравнений, содержащих эти координаты, то число независимых координат будет меньше на число этих связей.

- все радиус векторы.

, , где k – число связей.

Такие связи называются голономными. Если присутствует время (t) в уравнениях, то связи – нестационарные.

Для вычисления числа степеней свободы можем записать формулу:

Любые независимые переменные, полностью определяющие пространственное положение системы, называются обобщёнными координатами.

Виды координат:

Сферические .

Декартовы .

И другие.

Графическое пояснение:

Вывод данных формул элементарен по Рис.1

- i-тая компонента.

Рассмотрим пример:

Дан математический маятник (Рис.2).

- это n-мерный вектор. Здесь n=1, и уравнения связи имеют вид:

где .

- уравнение связи.

Определим число степеней свободы:

Тогда число степеней свободы равно единице.

§2. Описание эволюции системы в конфигурационном пространстве (кп).

КП – это n – мерное пространство обобщенных координат.

- радиус вектор в D-пространстве.

Реальному пространству ставим в соответствие КП

→

КП – служит для технического упрощения решения задач. Одна точка в КП изображает положение системы N материальных точек в реальном D-мерном пространстве.

С истема материальных точек находится во внешнем поле, и они могут взаимодействовать между собой, поэтому движутся по каким-то траекториям. Изменение реальных координат приводит к изменению обобщенных координат. Движение реальных точек приводит к движению изображающей точки. Таким образом, эволюция системы (движение точек в реальном пространстве) описывается движением изображающей точки в КП. В результате в КП получаем траекторию.

Говоря о траектории системы, будем иметь в виду траекторию изображающей точки в КП.

Эволюция системы – это движение в реальном пространстве реальных точек по реальным траекториям.

- -тая обобщённая координата, _.

Итак, имеется траектория в КП. Проведём касательный вектор - обобщенная скорость.

Чтобы описать движение системы надо знать положение точки в любой момент времени – закон движения:

Найти такую зависимость можно из закона Ньютона:

(2.1)

Решением этого уравнения будет некоторый закон движения .

Уравнение (2.1) – дифференциальное уравнение второго порядка, следовательно необходимо два начальных условия:

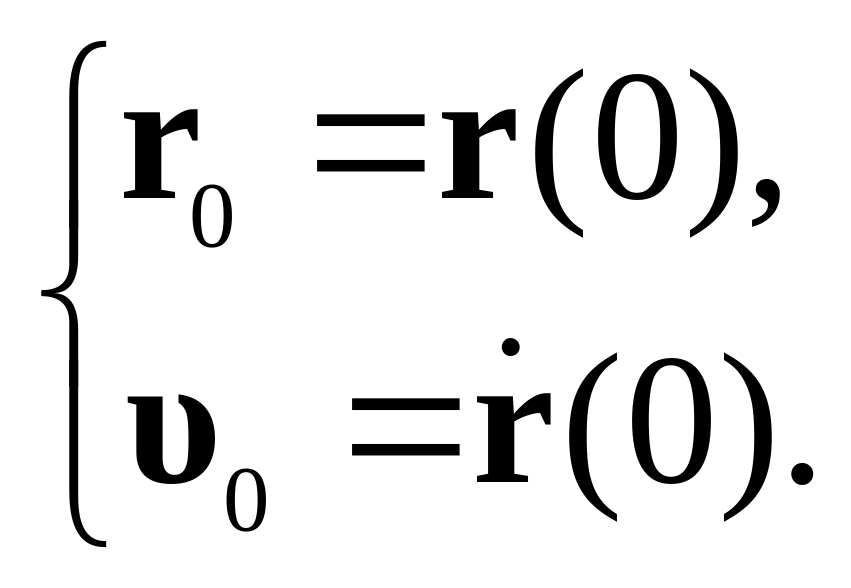(2.2)

Уравнений должно быть столько, сколько степеней свободы.

Переменные вида (2.2) называются динамическими переменными – это координаты и скорости в данный момент времени. и - также динамические переменные. Зная и мы задаём механическое состояние системы в начальный момент времени.

Зная все силы, действующие на рассматриваемую систему, можно построить траекторию движения, если при этом решить уравнение движения.