17. Точечные оценки параметров (математическое ожидание и др.).

1. Среднее значение (математическое ожидание): .

2. Несмещенная (исправленная) дисперсия: .

3. Несмещенное среднеквадратическое отклонение: .

4. Коэффициент вариации: .

18. Интервальные оценки параметров трафика (доверительные интервалы).

Доверительный интервал представляет собой диапазон, для которого можно утверждать, с заданной вероятностью , называемой степенью доверия (или надежностью оценки), что он будет содержать оцениваемый параметр.

Доверительный интервал имеет следующую структуру: Точечная оценка ± Фактор надежности × Ошибка

• Точечная оценка – точечная оценка параметра (значение выборочной статистики).

• Фактор надежности – коэффициент, основанный на предполагаемом распределении точечной оценки и степени доверия для доверительного интервала.

• Ошибка – стандартная ошибка выборочной статистики, значение которой получено с помощью точечной оценки.

Доверительный интервал через медиану и СКО (используется редко): .

Основная процедура для расчета:

1. Определение выборочного среднего .

2. Если распределение не отлично от нормального (-оценка) и СКО известно:

   1. Главная формула: , где – надежность оценки (в районе 0.95-0.99), – оценка для уровня значимости (значение аргумента функции Лапласа, по таблице), – объем выборки.

   2. Находим значение функции Лапласа и аргумент по этому значению: , .

   3. Доверительный интервал: .

3. Если распределение отлично от нормального (t-распределение) или СКО неизвестно:

   1. Главная формула: , где – плотность распределения Стьюдента, – объем выборки, – исправленное СКО выборки, – критерий Стьюдента для уровня статистической значимости 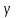и количества степеней свободы (по таблице).

   2. Находим 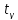из таблицы значений .

   3. Доверительный интервал: .

Пример.

7 измерений. Даны: среднее арифметическое – 30, выборочная дисперсия – 36, надежность – 0.99.

. . . . .

Доверительный интервал: .

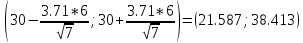19. Гистограммы. Интервалы между пакетами, длина пакетов. Смысловое значение гистограмм. Функции плотности вероятности и функции распределения.

Гистограмма — способ графического представления табличных данных. Количественные соотношения некоторого показателя представлены в виде прямоугольников, площади которых пропорциональны.

	Среднее значение задержки Где – значение -той задержки, n – количество измерений. Джиттер или среднее отклонение Коэффициент вариации:
Функция распределения

Плотность вероятности — один из способов задания распределения случайной величины, который характеризует сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).

Функция распределения — функция, характеризующая вероятность того, что случайная величина примет значение, меньшее или равное , где — произвольное действительное число.

Примеры абсолютно непрерывных распределений
Многомерное нормальное распределение Непрерывное равномерное распределение Нормальное распределение	Распределение Парето Распределение Стьюдента Экспоненциальное распределение

Показательный закон распределения (пример)

Плотность вероятности	Функция распределения