- •Математические модели в сетях связи Экзаменационные вопросы и ответы
- •1. Моделирование сетей связи, задачи моделирования, виды моделей. Математические модели сетей связи: назначение, области применения (предметная область).
- •Структура сети связи
- •2. Сеть связи как система массового обслуживания. Основные процессы в сети связи, показатели (параметры) функционирования сети связи.
- •3. Показатели качества обслуживания трафика. Понятия потерь (для сетей с кк и кп), задержки доставки данных, вариации задержки (джиттера).
- •4. Обозначения систем массового обслуживания по Кендаллу-Башарину.
- •5. Модель трафика как потока заявок. Понятие случайного потока. Характеристики потока.
- •6. Простейший поток заявок – математическая модель, основные свойства простейшего потока.
- •7. Случайный процесс. Понятие самоподобного трафика, коэффициент Херста, метод оценки коэффициента Херста.
- •8. Понятие абонентской нагрузки. Удельная абонентская нагрузка. Поступающая (производимая), обслуженная, потерянная нагрузка.
- •9. Модель сети с кк как системы массового обслуживания: система м/m/V при дисциплине обслуживания с потерями. Постановка задачи, оценка потерь в сети связи, 1 формула Эрланга.
- •10. Сети с кп. Дисциплины обслуживания заявок (пакетов), модели обслуживания, показатели качества. Система м/m/V (до с ожиданием), 2 формула Эрланга.
- •11. Формула Полячека-Хинчина. Область применения, параметры. Частные случаи для моделей m/m/1 и m/d/1. Время ожидания в очереди, время доставки сообщения (пакета).
- •Свертка:
- •16. Измерения параметров трафика. Объекты измерений, анализируемые параметры, план измерений.
- •Объект измерений:
- •17. Точечные оценки параметров (математическое ожидание и др.).
- •18. Интервальные оценки параметров трафика (доверительные интервалы).
- •19. Гистограммы. Интервалы между пакетами, длина пакетов. Смысловое значение гистограмм. Функции плотности вероятности и функции распределения.
- •20. Имитационное моделирование. Принцип построения дискретных событийных моделей. Упрощенная структура системы моделирования и алгоритм функционирования.
- •21. Получение потока событий с заданными свойствами. Получение случайных чисел с заданной функцией распределения. Метод обратной функции.
- •22. Расчет необходимой пропускной способности канала (линии связи) на примере услуг VoIp.
- •23. Задачи динамического программирования. Общее определение подхода к решению задачи. Пример постановки задачи, решаемой методом динамического программирования.
- •24. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Краскала.
- •25. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Прима.
- •26. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум расстояний до всех вершин графа (узлов сети) – поиск центра графа.
- •27. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум суммы расстояний до всех вершин графа (узлов сети) – поиск медианы графа.
- •28. Кластерный анализ, постановка задачи кластеризации. Алгоритм forel.
- •29. Кластерный анализ, постановка задачи кластеризации. Алгоритм k-средних.
- •30. Надежность сети связи, общие определения. Коэффициент готовности сети связи.
- •31. Надежность простейших сетевых структур. Оценка коэффициента готовности (вероятности исправного состояния) для параллельной и последовательной структур, метод декомпозиции.
- •36. Задачи прогнозирования развития технологий связи (проникновения). Основные характеристики уровня развития. Логистическая модель прогнозирования (логистическая регрессия).
- •38. Пример постановки задачи оптимизации надежности сети связи (максимум надежности).
- •39. Задачи оптимизации. Безусловная оптимизация. Условная оптимизация.
- •40. Экстремумы функций: определения локального и глобального экстремумов.
- •41. Безусловная оптимизация. Необходимые и достаточные условия существования экстремума функции нескольких переменных.
- •42. Условная оптимизация. Метод множителей Лагранжа.
- •43. Условная оптимизация. Условия Каруша-Куна-Таккера.
- •44. Численные методы оптимизации. Общая структура алгоритма. Привести примеры численных методов условной и безусловной оптимизации.
- •45. Оптимизация функции одной переменной. Метод дихотомии.
- •46. Оптимизация функции одной переменной. Метод золотого сечения.
- •47. Оптимизация функции нескольких переменных. Безусловная оптимизация. Покоординатный спуск.
- •48. Оптимизация функции нескольких переменных. Безусловная оптимизация. Симплекс метод Нелдера-Мида (поиск по деформируемому многограннику).
- •49. Оптимизация функции нескольких переменных. Условная оптимизация. Метод штрафных функций.
- •50. Оптимизация функции нескольких переменных. Невыпуклые функции. Эволюционный метод (генетический алгоритм).
42. Условная оптимизация. Метод множителей Лагранжа.
Математическое программирование – это область математики, разрабатывающая теорию, численные методы решения многомерных задач с ограничениями. В отличие от классической математики, математическое программирование занимается математическими методами решения задач нахождения наилучших вариантов из всех возможных.
|
Условная оптимизация. Метод множителей Лагранжа |
|
Пусть задана
функция нескольких
Требуется
найти экстремумы
|
|
Необходимые условия существования локального экстремума Функция Лагранжа:
Если точка
|
|
I. Достаточные условия существования локального экстремума (из лекций) Если
где
При всех
ненулевых
То
|
|
II. Достаточные условия существования локального экстремума (из интернета4) Окаймленный Гессиан:
Теорема 1 (достаточное
условие минимума). Пусть в точке
(означает,
что все миноры
Теорема 2 (достаточное
условие максимума). Пусть в точке
(означает, что в последовательности
миноров
|
|
Пример Мат. модель:
Задача Минимизировать функцию
Решение Перепишем условия в
виде
Составим функцию Лагранжа:
Составим систему:
Найдём
Составим окаймленный Гессиан:
|
|
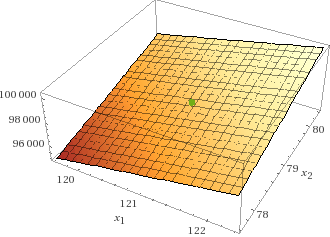
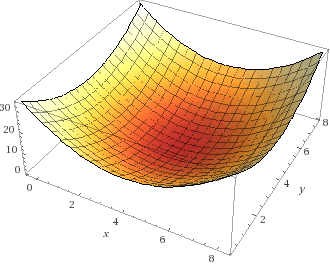
Wolfram Alpha:
|
43. Условная оптимизация. Условия Каруша-Куна-Таккера.
|
Выпуклое программирование – раздел нелинейного программирования, совокупность методов решения нелинейных экстремальных задач с выпуклыми целевыми функциями и выпуклыми системами ограничений. Пусть функция
Тогда каковы бы ни
были числа
Т. е.
Если функция
Многие задачи
оптимизации можно привести к этой
стандартной форме. Например, задача
максимизации вогнутой функции
Свойства выпуклой функции:
|
||||||||
|
Условия Каруша-Куна-Таккера (ККТ)5 Метод является обобщением метода множителей Лагранжа. В отличие от него, ограничения, накладываемые на переменные, представляют собой не уравнения, а неравенства. Пусть задана непрерывно
дифференцируемая выпуклая функция
Требуется найти
экстремумы
Функция Лагранжа:
Необходимые и достаточные условия существования минимума Точка
|
||||||||
|
Пример
Задача Найти
минимизировать
Ограничения:
Решение Перепишем условия так, чтобы справа был нуль:
Составим функцию Лагранжа:
Выписываем условия Каруша-Куна-Таккера:
Рассмотрим
4 случая (
В результате
получена единственная точка
Точка
удовлетворяет необходимым и достаточным
условиям, значит
|
||||||||
|
Wolfram
Alpha: |
||||||||

 переменных
переменных
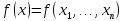 .
. при заданных ограничениях:
при заданных ограничениях: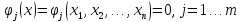
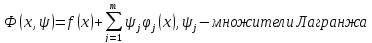
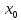 является локальным экстремумом и в
окрестности этой точки функции
является локальным экстремумом и в
окрестности этой точки функции
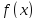 и
и
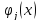 непрерывно дифференцируемы, то в этой
точке выполняются условия:
непрерывно дифференцируемы, то в этой
точке выполняются условия: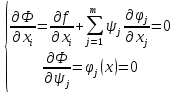
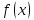 и
и
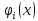 дважды дифференцируемы в точке
дважды дифференцируемы в точке
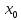 и в этой точке выполняются условия
и в этой точке выполняются условия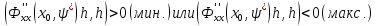
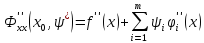
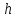 ,
удовлетворяющих условиям
,
удовлетворяющих условиям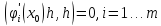
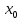 строгий локальный минимум (максимум)
строгий локальный минимум (максимум)
 при заданных ограничениях.
при заданных ограничениях.
 – главный минор матрицы
– главный минор матрицы
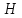 ,
образованный строками и столбцами
,
образованный строками и столбцами
 .
.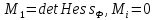 ,
при
,
при
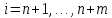
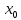 ранг матрицы
ранг матрицы
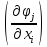 максимален и эта точка удовлетворяет
необходимым условиям наличия экстремума.
Тогда достаточным условием локального
минимума в задаче (
максимален и эта точка удовлетворяет
необходимым условиям наличия экстремума.
Тогда достаточным условием локального
минимума в задаче (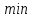 )
является выполнение неравенств:
)
является выполнение неравенств: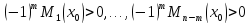
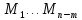 имеют знак
имеют знак
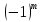 .
. ранг матрицы
ранг матрицы
 максимален и эта точка удовлетворяет
необходимым условиям наличия экстремума.
Тогда достаточным условием локального
максимума в задаче (
максимален и эта точка удовлетворяет
необходимым условиям наличия экстремума.
Тогда достаточным условием локального
максимума в задаче (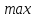 )
является выполнение неравенств:
)
является выполнение неравенств: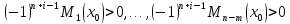
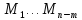 есть знакочередование, начиная со
знака
есть знакочередование, начиная со
знака
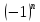 .
.
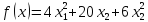 ,
,
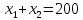 ,
,
 ,
,
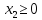 ,.
,.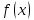 .
.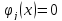 :
: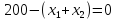
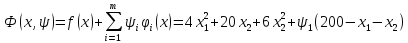
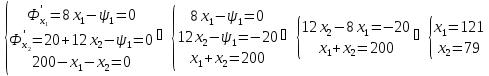
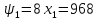 .
.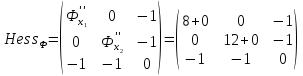
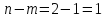 .
Рассматриваем только
.
Рассматриваем только
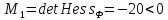 .
Минимум по достаточному условию.
.
Минимум по достаточному условию.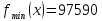
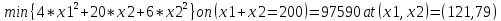
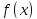 является выпуклой на некотором
промежутке
является выпуклой на некотором
промежутке
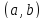 и числа
и числа
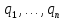 таковы, что
таковы, что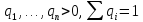
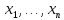 из промежутка
из промежутка
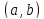 ,
выполняется неравенство:
,
выполняется неравенство: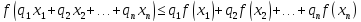
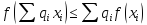
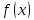 вогнута (выпукла вверх), то знак в
неравенстве меняется на противоположный.
вогнута (выпукла вверх), то знак в
неравенстве меняется на противоположный.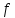 может быть переформулирована
эквивалентно как задача минимизации
выпуклой функции
может быть переформулирована
эквивалентно как задача минимизации
выпуклой функции
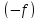 ,
так что о задаче максимизации вогнутой
функции на выпуклом множестве часто
говорят как о задаче выпуклого
программирования.
,
так что о задаче максимизации вогнутой
функции на выпуклом множестве часто
говорят как о задаче выпуклого
программирования.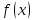 и
и
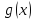 выпуклы, то их линейная комбинация
тоже выпуклая функция;
выпуклы, то их линейная комбинация
тоже выпуклая функция;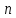 переменных
переменных
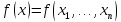 .
.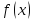 при заданных
при заданных
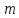 ограничениях в виде выпуклых функций
ограничениях в виде выпуклых функций
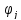 :
: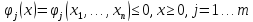
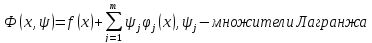
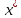 при наложенных ограничениях – решение
задачи.
при наложенных ограничениях – решение
задачи.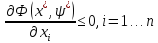
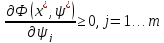
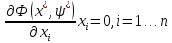
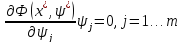
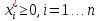
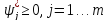
 .
.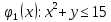 [ограничения задачи]
[ограничения задачи]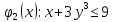 [ограничения задачи]
[ограничения задачи]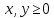 [стандартные ограничения]
[стандартные ограничения]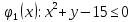
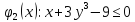
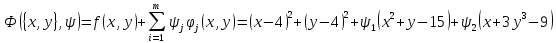
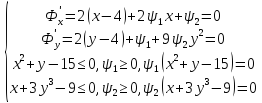
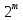 случаев для рассмотрения):
случаев для рассмотрения):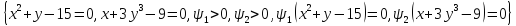
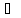 .
Решая систему, получаем
.
Решая систему, получаем
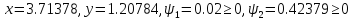 .
.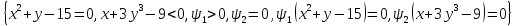
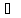 .
Корней нет.
.
Корней нет.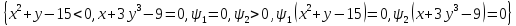
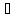 .
Корней нет.
.
Корней нет.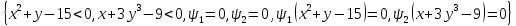
 .
Корней нет.
.
Корней нет.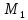 :
:
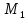 — минимум
— минимум
 для заданных условий.
для заданных условий.