
- •Математические модели в сетях связи Экзаменационные вопросы и ответы
- •1. Моделирование сетей связи, задачи моделирования, виды моделей. Математические модели сетей связи: назначение, области применения (предметная область).
- •Структура сети связи
- •2. Сеть связи как система массового обслуживания. Основные процессы в сети связи, показатели (параметры) функционирования сети связи.
- •3. Показатели качества обслуживания трафика. Понятия потерь (для сетей с кк и кп), задержки доставки данных, вариации задержки (джиттера).
- •4. Обозначения систем массового обслуживания по Кендаллу-Башарину.
- •5. Модель трафика как потока заявок. Понятие случайного потока. Характеристики потока.
- •6. Простейший поток заявок – математическая модель, основные свойства простейшего потока.
- •7. Случайный процесс. Понятие самоподобного трафика, коэффициент Херста, метод оценки коэффициента Херста.
- •8. Понятие абонентской нагрузки. Удельная абонентская нагрузка. Поступающая (производимая), обслуженная, потерянная нагрузка.
- •9. Модель сети с кк как системы массового обслуживания: система м/m/V при дисциплине обслуживания с потерями. Постановка задачи, оценка потерь в сети связи, 1 формула Эрланга.
- •10. Сети с кп. Дисциплины обслуживания заявок (пакетов), модели обслуживания, показатели качества. Система м/m/V (до с ожиданием), 2 формула Эрланга.
- •11. Формула Полячека-Хинчина. Область применения, параметры. Частные случаи для моделей m/m/1 и m/d/1. Время ожидания в очереди, время доставки сообщения (пакета).
- •Свертка:
- •16. Измерения параметров трафика. Объекты измерений, анализируемые параметры, план измерений.
- •Объект измерений:
- •17. Точечные оценки параметров (математическое ожидание и др.).
- •18. Интервальные оценки параметров трафика (доверительные интервалы).
- •19. Гистограммы. Интервалы между пакетами, длина пакетов. Смысловое значение гистограмм. Функции плотности вероятности и функции распределения.
- •20. Имитационное моделирование. Принцип построения дискретных событийных моделей. Упрощенная структура системы моделирования и алгоритм функционирования.
- •21. Получение потока событий с заданными свойствами. Получение случайных чисел с заданной функцией распределения. Метод обратной функции.
- •22. Расчет необходимой пропускной способности канала (линии связи) на примере услуг VoIp.
- •23. Задачи динамического программирования. Общее определение подхода к решению задачи. Пример постановки задачи, решаемой методом динамического программирования.
- •24. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Краскала.
- •25. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Прима.
- •26. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум расстояний до всех вершин графа (узлов сети) – поиск центра графа.
- •27. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум суммы расстояний до всех вершин графа (узлов сети) – поиск медианы графа.
- •28. Кластерный анализ, постановка задачи кластеризации. Алгоритм forel.
- •29. Кластерный анализ, постановка задачи кластеризации. Алгоритм k-средних.
- •30. Надежность сети связи, общие определения. Коэффициент готовности сети связи.
- •31. Надежность простейших сетевых структур. Оценка коэффициента готовности (вероятности исправного состояния) для параллельной и последовательной структур, метод декомпозиции.
- •36. Задачи прогнозирования развития технологий связи (проникновения). Основные характеристики уровня развития. Логистическая модель прогнозирования (логистическая регрессия).
- •38. Пример постановки задачи оптимизации надежности сети связи (максимум надежности).
- •39. Задачи оптимизации. Безусловная оптимизация. Условная оптимизация.
- •40. Экстремумы функций: определения локального и глобального экстремумов.
- •41. Безусловная оптимизация. Необходимые и достаточные условия существования экстремума функции нескольких переменных.
- •42. Условная оптимизация. Метод множителей Лагранжа.
- •43. Условная оптимизация. Условия Каруша-Куна-Таккера.
- •44. Численные методы оптимизации. Общая структура алгоритма. Привести примеры численных методов условной и безусловной оптимизации.
- •45. Оптимизация функции одной переменной. Метод дихотомии.
- •46. Оптимизация функции одной переменной. Метод золотого сечения.
- •47. Оптимизация функции нескольких переменных. Безусловная оптимизация. Покоординатный спуск.
- •48. Оптимизация функции нескольких переменных. Безусловная оптимизация. Симплекс метод Нелдера-Мида (поиск по деформируемому многограннику).
- •49. Оптимизация функции нескольких переменных. Условная оптимизация. Метод штрафных функций.
- •50. Оптимизация функции нескольких переменных. Невыпуклые функции. Эволюционный метод (генетический алгоритм).
11. Формула Полячека-Хинчина. Область применения, параметры. Частные случаи для моделей m/m/1 и m/d/1. Время ожидания в очереди, время доставки сообщения (пакета).
 — интенсивность нагрузки,
— интенсивность нагрузки,
 — среднее время ожидания в очереди,
— среднее время ожидания в очереди,
 — среднее время обслуживания заявки
— среднее время обслуживания заявки

 — время ожидания в очереди
— время ожидания в очереди
M/M/1:
 ;
M/D/1:
;
M/D/1:
 ;
;
|
M/M/1 |
M/D/1 |
GI/G/1 |
|
|
|
Неравенство Кингмана:
|
|
Аппроксимация Маршалла:
|
||
|
|
||

 — среднеквадратическое отклонение
времени между заявками
— среднеквадратическое отклонение
времени между заявками
 — среднеквадратическое отклонение
времени обслуживания
— среднеквадратическое отклонение
времени обслуживания
12. Неравенство Кингмана. Параметры, область применения.
Неравенство Кингмана:

 — среднее время ожидания в очереди
— среднее время ожидания в очереди
 — интенсивность нагрузки
— интенсивность нагрузки
 — среднее время обслуживания заявки
— среднее время обслуживания заявки
 — среднеквадратическое отклонение
времени между заявками
— среднеквадратическое отклонение
времени между заявками
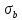 — среднеквадратическое отклонение
времени обслуживания
— среднеквадратическое отклонение
времени обслуживания
 — время доставки сообщения (пакета)
— время доставки сообщения (пакета)
13. Аппроксимация Маршалла. Параметры, область применения.
Аппроксимация Маршалла:

 — среднее время ожидания в очереди
— среднее время ожидания в очереди
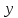 — интенсивность нагрузки
— интенсивность нагрузки
 — среднее время обслуживания заявки
— среднее время обслуживания заявки
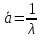 — среднее время между заявками
— среднее время между заявками
 — среднеквадратическое отклонение
времени между заявками
— среднеквадратическое отклонение
времени между заявками
 — среднеквадратическое отклонение
времени обслуживания
— среднеквадратическое отклонение
времени обслуживания
 — время доставки сообщения (пакета)
— время доставки сообщения (пакета)
14. Оценка потерь в сети связи на маршруте предоставления услуги
Вероятность
того, что хотя бы одно обслуживающее
устройство откажет:
 ,
где
,
где
 — вероятность отказа
— вероятность отказа
 -того
обслуживающего устройства.
-того
обслуживающего устройства.
|
M/M/1/K |
GI/G/1/K |
|
|
|
|
|
|
|
|
|
15. Последовательность СМО. Характеристики обслуживания заявки последовательностью СМО. Функция распределения времени доставки.
|
Последовательность СМО с потерями |
Последовательность СМО с ожиданием |
|
|
|
|
|
|
Если
 и
и
 независимые случайные числа, имеющие
функции плотности вероятности
независимые случайные числа, имеющие
функции плотности вероятности
 и
и
 ,
то их сумма
,
то их сумма
 случайное число c плотностью вероятности
случайное число c плотностью вероятности
 .
.
Свертка:
Если
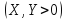 :
:

Преобразование Лапласа:
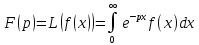
Обратное преобразование Лапласа:

(или заменяется вычислением вычетов по полюсам функции как представлено далее в примере)
|
Пример |
|
|
|
|
16. Измерения параметров трафика. Объекты измерений, анализируемые параметры, план измерений.
Цель измерений трафика: получение сведений о характеристиках и параметрах процесса поступления и обслуживания заявок (вызовов или пакетов).
Цель измерений QoS: получение сведений о характеристиках процесса обслуживания заявок (вызовов или пакетов)
-
Объект измерений:
-
Абонент (группа абонентов): измерения абонентского трафика;
-
Линия связи (пучок соединительных линий): измерения нагрузки;
-
Направление связи: измерения по направлениям связи;
-
Коммутатор: измерения на коммутаторе;
Измеряемые параметры:
-
Интенсивность заявок (интенсивность вызовов, интенсивность поступления пакетов);
-
Продолжительность обслуживания (продолжительность вызова, длина пакета);
-
Интервалы времени между заявками;
-
Зависимость нагрузки от времени;
-
Зависимость продолжительности обслуживания от времени (суток, недели, сезона, года);
-
Зависимость продолжительности обслуживания от вида услуги;
-
Зависимость объема трафика от времени;
-
Вероятность потерь (коэффициент потерь);
-
Задержка доставки пакета данных;
-
Вариация задержки доставки пакета данных (джиттер);
-
Коэффициент ошибок;
-
Время установления соединения;
План проведения измерений:
-
Время проведения измерений (дни, сезоны);
-
Продолжительность измерений (непрерывные, периодические);
-
Объем выборки (репрезентативность результата);
Обработка результатов:
-
Точечные оценки;
-
Интервальные оценки;
-
Распределения;
-
Тренды;
-
Другие зависимости.





 — время доставки сообщения (пакета)
— время доставки сообщения (пакета)












