4. Обозначения систем массового обслуживания по Кендаллу-Башарину.

A	B	C	K	N	D
Поступающий поток вызовов	Закон распределения времени обслуживания	Структура системы обслуживания (число обслуживающих устройств)	Дисциплина обслуживания	Способ выбора из очереди	Сведения о порядке выбора свободного канала
M — простейший поток D — детерминированный поток Ek — поток Эрланга GI — общий вид распределения	M — простейший поток D — детерминированный поток Ek — поток Эрланга G — общий вид распределения	S — любая структура V — число приборов	LL (lossless) — без потерь L (loss) — с явными потерями W — с ожиданием R — с повторением	SP — равновероятный FF — первым пришел, первым ушел LF — последним пришел, первым ушел PR — приоритетный	S — последовательный R — случайный

5. Модель трафика как потока заявок. Понятие случайного потока. Характеристики потока.

Поток трафика (пакетов, вызовов, …) — последовательность событий, происходящих через какие-либо интервалы или в какие-либо моменты времени.

Следует различать детерминированный и случайный потоки вызовов.

Детерминированный поток вызовов — последовательность вызовов, в которой вызовы поступают в определенные, строго фиксированные неслучайные моменты или через определенные, строго фиксированные, неслучайные промежутки времени.

Случайный поток вызовов отличается от детерминированного тем и только тем, что моменты поступления вызовов и промежутки времени между вызовами являются не строго фиксированными, а случайными величинами.

Детерминированные потоки являются частным случаем случайных потоков.

В теории массового обслуживания и теории телетрафика основное внимание уделяется рассмотрению случайных потоков вызовов.

Поток вызовов может быть определен тремя эквивалентными способами:

1. Последовательностью моментов времени ;

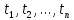2. Последовательностью промежутков времени между моментами событий ;

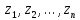3. Последовательностью чисел 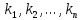, определяющих количество вызовов, поступающих в течение заданных отрезков времени , ,..., .

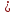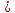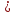Для задания случайных потоков, как и любых других случайных величин и процессов, используются функции распределения.

Функция распределения вероятностей некоторой случайной величины X:

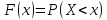
Математическое ожидание числа вызовов, поступающих в интервале времени 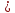, называется ведущей функцией потока. Это неотрицательная, неубывающая функция, и в практических задачах принимает конечное значение.

Потоки с непрерывной ведущей функцией называются регулярными, а со ступенчатой сингулярными.

Свойства потока:

• Стационарность. Поток вызовов является стационарным, если при любом 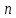совместный закон распределения числа вызовов за промежутки времени , ,...,

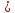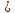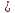
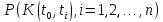
зависит только от длины промежутков времени и не зависит от момента .

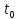Т.е. независимо от того, где на оси времени расположен промежуток времени 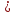, вероятность поступления 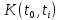вызовов одна и та же.

Другими словами, вероятность появления 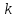событий за промежуток времени длительностью есть функция, зависящая только от 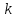и (и 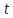не зависящая от начала отсчета).

• Ординарность. Обозначим через 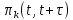вероятность поступления 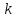и более вызовов за промежуток 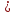. Поток вызовов является ординарным, если при :

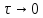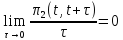
Другими словами, появление двух или более событий за малый промежуток времени практически невозможно.

• Отсутствие последействия. Поток вызовов является потоком без последействия, если вероятность поступления 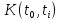вызовов за промежутки 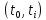, не зависит от вероятностного процесса поступления вызовов до момента .

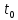Другими словами, вероятность появления 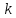событий в любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка.

Характеристики потоков заявок

Основные характеристики потока вызовов:

• Ведущая функция потока — математическое ожидание числа вызовов, поступающих в промежутке времени

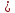
• Параметр потока — характеристика потока вызывающих моментов, которая относится не ко всему отрезку 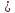, а лишь к фиксированному моменту 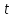. Предел отношения вероятности поступления хотя бы одного вызова за время 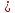к длине этого отрезка времени :

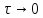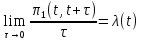
Параметр потока есть плотность вероятности наступления вызывающего момента в момент 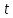. Тогда вероятность поступления одного и более вызовов за время :

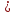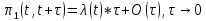
Для стационарного потока, вероятность поступления определенного числа вызовов за некоторый промежуток времени одна и та же и не зависит от месторасположения на оси времени этого промежутка. Следовательно, и плотность вероятности поступления вызовов стационарного потока, т. е. его параметр 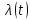, есть величина постоянная, не зависящая от момента t, т. е. :

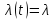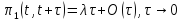
• Интенсивность потока — математическое ожидание числа вызовов, поступающих в единицу времени.