
- •Математические модели в сетях связи Экзаменационные вопросы и ответы
- •1. Моделирование сетей связи, задачи моделирования, виды моделей. Математические модели сетей связи: назначение, области применения (предметная область).
- •Структура сети связи
- •2. Сеть связи как система массового обслуживания. Основные процессы в сети связи, показатели (параметры) функционирования сети связи.
- •3. Показатели качества обслуживания трафика. Понятия потерь (для сетей с кк и кп), задержки доставки данных, вариации задержки (джиттера).
- •4. Обозначения систем массового обслуживания по Кендаллу-Башарину.
- •5. Модель трафика как потока заявок. Понятие случайного потока. Характеристики потока.
- •6. Простейший поток заявок – математическая модель, основные свойства простейшего потока.
- •7. Случайный процесс. Понятие самоподобного трафика, коэффициент Херста, метод оценки коэффициента Херста.
- •8. Понятие абонентской нагрузки. Удельная абонентская нагрузка. Поступающая (производимая), обслуженная, потерянная нагрузка.
- •9. Модель сети с кк как системы массового обслуживания: система м/m/V при дисциплине обслуживания с потерями. Постановка задачи, оценка потерь в сети связи, 1 формула Эрланга.
- •10. Сети с кп. Дисциплины обслуживания заявок (пакетов), модели обслуживания, показатели качества. Система м/m/V (до с ожиданием), 2 формула Эрланга.
- •11. Формула Полячека-Хинчина. Область применения, параметры. Частные случаи для моделей m/m/1 и m/d/1. Время ожидания в очереди, время доставки сообщения (пакета).
- •Свертка:
- •16. Измерения параметров трафика. Объекты измерений, анализируемые параметры, план измерений.
- •Объект измерений:
- •17. Точечные оценки параметров (математическое ожидание и др.).
- •18. Интервальные оценки параметров трафика (доверительные интервалы).
- •19. Гистограммы. Интервалы между пакетами, длина пакетов. Смысловое значение гистограмм. Функции плотности вероятности и функции распределения.
- •20. Имитационное моделирование. Принцип построения дискретных событийных моделей. Упрощенная структура системы моделирования и алгоритм функционирования.
- •21. Получение потока событий с заданными свойствами. Получение случайных чисел с заданной функцией распределения. Метод обратной функции.
- •22. Расчет необходимой пропускной способности канала (линии связи) на примере услуг VoIp.
- •23. Задачи динамического программирования. Общее определение подхода к решению задачи. Пример постановки задачи, решаемой методом динамического программирования.
- •24. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Краскала.
- •25. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Прима.
- •26. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум расстояний до всех вершин графа (узлов сети) – поиск центра графа.
- •27. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум суммы расстояний до всех вершин графа (узлов сети) – поиск медианы графа.
- •28. Кластерный анализ, постановка задачи кластеризации. Алгоритм forel.
- •29. Кластерный анализ, постановка задачи кластеризации. Алгоритм k-средних.
- •30. Надежность сети связи, общие определения. Коэффициент готовности сети связи.
- •31. Надежность простейших сетевых структур. Оценка коэффициента готовности (вероятности исправного состояния) для параллельной и последовательной структур, метод декомпозиции.
- •36. Задачи прогнозирования развития технологий связи (проникновения). Основные характеристики уровня развития. Логистическая модель прогнозирования (логистическая регрессия).
- •38. Пример постановки задачи оптимизации надежности сети связи (максимум надежности).
- •39. Задачи оптимизации. Безусловная оптимизация. Условная оптимизация.
- •40. Экстремумы функций: определения локального и глобального экстремумов.
- •41. Безусловная оптимизация. Необходимые и достаточные условия существования экстремума функции нескольких переменных.
- •42. Условная оптимизация. Метод множителей Лагранжа.
- •43. Условная оптимизация. Условия Каруша-Куна-Таккера.
- •44. Численные методы оптимизации. Общая структура алгоритма. Привести примеры численных методов условной и безусловной оптимизации.
- •45. Оптимизация функции одной переменной. Метод дихотомии.
- •46. Оптимизация функции одной переменной. Метод золотого сечения.
- •47. Оптимизация функции нескольких переменных. Безусловная оптимизация. Покоординатный спуск.
- •48. Оптимизация функции нескольких переменных. Безусловная оптимизация. Симплекс метод Нелдера-Мида (поиск по деформируемому многограннику).
- •49. Оптимизация функции нескольких переменных. Условная оптимизация. Метод штрафных функций.
- •50. Оптимизация функции нескольких переменных. Невыпуклые функции. Эволюционный метод (генетический алгоритм).
50. Оптимизация функции нескольких переменных. Невыпуклые функции. Эволюционный метод (генетический алгоритм).
Стохастические методы.
Целью разработки и использования данных методов является оптимизация невыпуклых функций.
Общего метода численной оптимизации невыпуклых функций не существует. Существуют лишь подходы, позволяющие на основании имеющихся сведений об оптимизируемой функции использовать те или иные методы, позволяющие с достаточной уверенностью находить оптимальные (или приемлемые) решения.
Оптимизацию невыпуклых функций называют многоэкстремальной оптимизацией.
Примеры методов оптимизации:
-
Слепой случайный поиск: поиск экстремума в заданной области путем проб в случайных точках области;
-
Локальный случайный поиск: поиск экстремума в заданной области путем проб в случайных точках, сосредоточенных вокруг некоторой базисной точки с последующим переходом к другой базисной точке;
-
Мультистартовый метод: многократный запуск метода поиска экстремума выпуклой функции из различных стартовых точек;
-
Эволюционный метод (генетический алгоритм): метод имитирующий процесс эволюции, происходящий в живой природе.
Генетический алгоритм (англ. genetic algorithm) — это стохастический эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём последовательного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию. Является разновидностью эволюционных вычислений (англ. evolutionary computation). Отличительной особенностью генетического алгоритма является акцент на использование оператора «скрещивания», который производит операцию рекомбинации решений-кандидатов, роль которой аналогична роли скрещивания в живой природе.
Предполагает имитацию процесса эволюции (различные реализации могут использовать различные приемы имитирующие этапы эволюционного процесса). Например:
-
Значения переменных (точка) – особь.
-
Значение функции в точке характеризует приспособленность особи (выживаемость).
Пусть задана
выпуклая функция
 переменных
переменных
 .
.
Данный метод предполагает следующие шаги:
-
Создание начальной популяции – множества особей, численность
 .
. -
Выбор родителей. Полагаем, что для появления новой особи требуются наследственные признаки двух других особей. Выбор может производится различными способами, например, случайно (панмиксия). Особи
 и
и
 .
. -
Рекомбинация. Передача наследственных признаков потомку. Существуют различные способы реализации данного шага. Например, вектор переменных можно рассматривать как набор генов, при этом одноименные гены родителей объединяются со случайными коэффициентами:
 ,
где
,
где
 – случайное число.
– случайное число.
-
Мутация. Случайное изменение наследственных признаков. Например,
 ,
где
,
где
 (дзета) – случайный коэффициент.
(дзета) – случайный коэффициент. -
Селекция. Новая особь помещается в популяцию на место наименее приспособленной особи, которая, освобождая позицию, погибает.
Сходимость. Процесс смены поколений повторяется пока на протяжении некоторого (заданного) числа поколений не будет происходить уменьшение (увеличение) значения целевой функции.
|
Пример (из лекции) Функция Экли
|
|
|
|
|
|
|
Найденное значение:
Размер популяции 50, число поколений 1000. Реальный экстремум:
|
|
Пример на C++ Программа с генетическим
алгоритмом поиска глобального минимума
функции двух переменных
Представлены вычисления следующих функций6:
|
|
// C++14 #define _USE_MATH_DEFINES #include <cmath> #include <algorithm> #include <iostream> #include <functional> #include <vector> #include <random> #include <stack> #include <iomanip> using namespace std;
template <class T> class GeneticAlgorithm { public: // Инициализация основных переменных в конструкторе GeneticAlgorithm(int number_of_population_members, double percent_of_best_ones_to_live, pair<T, T> section, std::function<T(T, T)> function, double probability) : number_of_population_members_(number_of_population_members), percent_of_best_ones_to_live_(percent_of_best_ones_to_live), section_(std::move(section)), function_(std::move(function)), probability_(probability) { std::random_device rd; random_gen_.seed(rd()); }
// Инициализирует популяцию void generateInitialPopulation() { population_x_ = createNewPopulation(); population_y_ = createNewPopulation(); }
// Создает и возвращает новую популяцию vector<T> createNewPopulation() { T minimum = section_.first; T maximum = section_.second; vector<T> result(number_of_population_members_); std::uniform_real_distribution<> real_dist(minimum, maximum); // Равномерное непрерывное распределение for (auto &k : result) { k = real_dist(random_gen_); } return result; }
// Фитнес-функция (или функция пригодности) // Возвращает пары векторов лучших популяций X и Y (отбор по проценту выживаемости) pair<vector<T>, vector<T>> getBestMembers() { vector<T> function_values(number_of_population_members_); auto tempX = population_x_.begin(); auto tempY = population_y_.begin(); for (auto &k : function_values) { k = function_(*( tempX++ ), *( tempY++ )); } Sort(function_values, population_x_, population_y_); // Сортировка Хоара в классе auto amount_of_best_values = static_cast<int>(function_values.size() * percent_of_best_ones_to_live_); return {vector<T>(population_x_.begin(), population_x_.begin() + amount_of_best_values), vector<T>(population_y_.begin(), population_y_.begin() + amount_of_best_values)}; }
// Мутация популяций void mutate() { auto minimal_population_x = *std::min(population_x_.begin(), population_x_.end()); auto minimal_population_y = *std::min(population_y_.begin(), population_y_.end()); std::normal_distribution<> normal_dist {0, min(probability_ * 1000, 0.001)}; // нормальное распределение for (auto &elem : population_x_) { elem += minimal_population_x * normal_dist(random_gen_); } for (auto &elem : population_y_) { elem += minimal_population_y * normal_dist(random_gen_); } }
// Рекомбинация (размножение) void crossover() { int population_x_length = population_x_.size(); std::uniform_int_distribution<> uniform_dist(0, population_x_length - 1); // Равномерное дискретное распределение population_x_.resize(number_of_population_members_); // Увеличение population_y_.resize(number_of_population_members_); // Увеличение for (int i = population_x_length; i < number_of_population_members_; ++i) { population_x_[i] = ( population_x_[uniform_dist(random_gen_)] + population_x_[uniform_dist(random_gen_)] ) / 2.0; population_y_[i] = ( population_y_[uniform_dist(random_gen_)] + population_y_[uniform_dist(random_gen_)] ) / 2.0; } }
// Поиск минимума функции (количество итераций в аргументах) T searchMinimum(int iterations) { generateInitialPopulation(); for (int i = 0; i < iterations; ++i) { auto temp_population = getBestMembers(); population_x_ = temp_population.first; population_y_ = temp_population.second; crossover(); mutate(); } auto minimumValueIndex = getMinimalValueIndex(); return function_(population_x_[minimumValueIndex], population_y_[minimumValueIndex]); }
// Получение индекса элемента с минимальным значением функции f(x, y) int getMinimalValueIndex() { vector<T> function_values(number_of_population_members_); auto tempX = population_x_.begin(), tempY = population_y_.begin(); for (auto &k : function_values) { k = function_(*( tempX++ ), *( tempY++ )); } return std::min(function_values.begin(), function_values.end()) - function_values.begin(); }
// Получение X и Y координаты минимума pair<T, T> getArgumentsOfMinimumValue() { auto minimum_value_index = getMinimalValueIndex(); return {population_x_[minimum_value_index], population_y_[minimum_value_index]}; }
GeneticAlgorithm(const GeneticAlgorithm &arg) = delete; GeneticAlgorithm &operator=(const GeneticAlgorithm &arg) = delete; GeneticAlgorithm &operator=(GeneticAlgorithm &arg) = delete; GeneticAlgorithm(GeneticAlgorithm &&arg) = delete;
private: int number_of_population_members_; // Количество популяций double percent_of_best_ones_to_live_; // Процент выживаемости (лучшие выживают, остальные погибают) pair<T, T> section_; // Ограничения областей определения std::function<T(T, T)> function_; // Функция, которую необходимо минимизировать double probability_; // Точность vector<T> population_x_; // Популяция X vector<T> population_y_; // Популяция Y std::mt19937 random_gen_; // Генератор рандомных чисел
// Итеративная быстрая сортировка Хоара для трехмерного массива по первому вектору functionValues static void Sort(vector<T> &functionValues, vector<T> &populationX, vector<T> &populationY) { int Left = 0, Right = functionValues.size() - 1, L2, R2; T PivotValue, Temp; std::stack<T> Lows, Highs; Lows.push(Left); Highs.push(Right); while (!Lows.empty()) { Left = Lows.top(); Lows.pop(); Right = Highs.top(); Highs.pop(); L2 = Left; R2 = Right; PivotValue = functionValues[( Left + Right ) / 2]; do { while (functionValues[L2] < PivotValue) { ++L2; } while (functionValues[R2] > PivotValue) { --R2; } if (L2 <= R2) { if (functionValues[L2] > functionValues[R2]) { std::swap(functionValues[L2], functionValues[R2]); std::swap(populationX[L2], populationX[R2]); std::swap(populationY[L2], populationY[R2]); } ++L2; if (R2 > 0) { --R2; } } } while (L2 <= R2); if (L2 < Right) { Lows.push(L2); Highs.push(Right); } if (R2 > Left) { Lows.push(Left); Highs.push(R2); } } } };
// Функция Экли double AckleyFunction(double x, double y) { return -20 * exp(-0.2 * sqrt(0.5 * ( x * x + y * y ))) - exp(0.5 * ( cos(2 * M_PI * x) + cos(2 * M_PI * y) )) + M_E + 20; }
// Функция Била double BealFunction(double x, double y) { return pow(1.5 - x + x * y, 2) + pow(2.25 - x + x * y * y, 2) + pow(2.625 - x + x * y * y * y, 2); }
// Функция Изома double IzomFunction(double x, double y) { return -cos(x) * cos(y) * exp(-pow(x - M_PI, 2) - pow(y - M_PI, 2)); }
// Функция Розенброка double RosenbrokFunction(double x, double y) { return ( 1.0 - x ) * ( 1.0 - x ) + 100.0 * ( y - x * x ) * ( y - x * x ); }
// Функция Шаффера-N2 double ShafferN2Function(double x, double y) { return 0.5 + (pow(sin(x * x - y * y), 2) - 0.5) / pow(1 + 0.001 * (x * x + y * y), 2); }
int main() { cout << setprecision(16); const double EPS = 1e-7; int numberOfPopulationMembers = 10000; int iterations = 10000; double percentOfBestOnesToLive = 0.8; pair<double, double> searchingSection = {-1, 4}; GeneticAlgorithm<double> GA_A(numberOfPopulationMembers, percentOfBestOnesToLive, searchingSection, AckleyFunction, EPS); { cout << "Ackley Function" << endl; auto minimumValue = GA_A.searchMinimum(iterations); auto minimumPoint = GA_A.getArgumentsOfMinimumValue(); cout << "Minimum: f(" << minimumPoint.first << ", " << minimumPoint.second << ") = " << minimumValue << endl; cout << "Real: f(0, 0) = 0" << endl << endl; } GeneticAlgorithm<double> GA_B(numberOfPopulationMembers, percentOfBestOnesToLive, searchingSection, BealFunction, EPS); { cout << "Beal Function" << endl; auto minimumValue = GA_B.searchMinimum(iterations); auto minimumPoint = GA_B.getArgumentsOfMinimumValue(); cout << "Minimum: f(" << minimumPoint.first << ", " << minimumPoint.second << ") = " << minimumValue << endl; cout << "Real: f(3, 0.5) = 0" << endl << endl; } GeneticAlgorithm<double> GA_I(numberOfPopulationMembers, percentOfBestOnesToLive, searchingSection, IzomFunction, EPS); { cout << "Izom Function" << endl; auto minimumValue = GA_I.searchMinimum(iterations); auto minimumPoint = GA_I.getArgumentsOfMinimumValue(); cout << "Minimum: f(" << minimumPoint.first << ", " << minimumPoint.second << ") = " << minimumValue << endl; cout << "Real: f(" << M_PI << ", " << M_PI << ") = -1" << endl << endl; } GeneticAlgorithm<double> GA_R(numberOfPopulationMembers, percentOfBestOnesToLive, searchingSection, RosenbrokFunction, EPS); { cout << "Rosenbrok Function" << endl; auto minimumValue = GA_R.searchMinimum(iterations); auto minimumPoint = GA_R.getArgumentsOfMinimumValue(); cout << "Minimum: f(" << minimumPoint.first << ", " << minimumPoint.second << ") = " << minimumValue << endl; cout << "Real: f(1, 1) = 0" << endl << endl; } GeneticAlgorithm<double> GA_S(numberOfPopulationMembers, percentOfBestOnesToLive, searchingSection, ShafferN2Function, EPS); { cout << "Shaffer-N2 Function" << endl; auto minimumValue = GA_S.searchMinimum(iterations); auto minimumPoint = GA_S.getArgumentsOfMinimumValue(); cout << "Minimum: f(" << minimumPoint.first << ", " << minimumPoint.second << ") = " << minimumValue << endl; cout << "Real: f(0, 0) = 0" << endl << endl; } }
|
|
Ackley Function Minimum: f(-5.98758489061304e-017, -2.48240045892338e-016) = 0 Real: f(0, 0) = 0
Beal Function Minimum: f(2.999222670167661, 0.5000279037180311) = 1.219544345334276e-006 Real: f(3, 0.5) = 0
Izom Function Minimum: f(3.140764183335173, 3.141758819721291) = -0.9999989290393152 Real: f(3.141592653589793, 3.141592653589793) = -1
Rosenbrok Function Minimum: f(0.9915841325064821, 0.9837831595975776) = 0.0001004277983007698 Real: f(1, 1) = 0
Shaffer-N2 Function Minimum: f(1.985576425992537e-007, 4.995542217822875e-007) = 2.220446049250313e-016 Real: f(0, 0) = 0 |
1 Ациклический граф: без циклов.
2 Связный граф: между любой парой вершин графа существует как минимум один путь (непосредственный / посредственный).
3 Громницкий В.С. Методы оптимизации. Курс лекций: Учебное пособие.
4 URL: http://meit.mgimo.ru/sites/default/files/Lecture_2_2.pdf
5 URL: https://projecteuclid.org/download/pdf_1/euclid.bsmsp/1200500249
6 Эти и другие мат. функции можно найти здесь: https://ru.wikipedia.org/wiki/Тестовые_функции_для_оптимизации






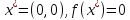
 в виде класса со свойствами и методами.
в виде класса со свойствами и методами.