
- •Математические модели в сетях связи Экзаменационные вопросы и ответы
- •1. Моделирование сетей связи, задачи моделирования, виды моделей. Математические модели сетей связи: назначение, области применения (предметная область).
- •Структура сети связи
- •2. Сеть связи как система массового обслуживания. Основные процессы в сети связи, показатели (параметры) функционирования сети связи.
- •3. Показатели качества обслуживания трафика. Понятия потерь (для сетей с кк и кп), задержки доставки данных, вариации задержки (джиттера).
- •4. Обозначения систем массового обслуживания по Кендаллу-Башарину.
- •5. Модель трафика как потока заявок. Понятие случайного потока. Характеристики потока.
- •6. Простейший поток заявок – математическая модель, основные свойства простейшего потока.
- •7. Случайный процесс. Понятие самоподобного трафика, коэффициент Херста, метод оценки коэффициента Херста.
- •8. Понятие абонентской нагрузки. Удельная абонентская нагрузка. Поступающая (производимая), обслуженная, потерянная нагрузка.
- •9. Модель сети с кк как системы массового обслуживания: система м/m/V при дисциплине обслуживания с потерями. Постановка задачи, оценка потерь в сети связи, 1 формула Эрланга.
- •10. Сети с кп. Дисциплины обслуживания заявок (пакетов), модели обслуживания, показатели качества. Система м/m/V (до с ожиданием), 2 формула Эрланга.
- •11. Формула Полячека-Хинчина. Область применения, параметры. Частные случаи для моделей m/m/1 и m/d/1. Время ожидания в очереди, время доставки сообщения (пакета).
- •Свертка:
- •16. Измерения параметров трафика. Объекты измерений, анализируемые параметры, план измерений.
- •Объект измерений:
- •17. Точечные оценки параметров (математическое ожидание и др.).
- •18. Интервальные оценки параметров трафика (доверительные интервалы).
- •19. Гистограммы. Интервалы между пакетами, длина пакетов. Смысловое значение гистограмм. Функции плотности вероятности и функции распределения.
- •20. Имитационное моделирование. Принцип построения дискретных событийных моделей. Упрощенная структура системы моделирования и алгоритм функционирования.
- •21. Получение потока событий с заданными свойствами. Получение случайных чисел с заданной функцией распределения. Метод обратной функции.
- •22. Расчет необходимой пропускной способности канала (линии связи) на примере услуг VoIp.
- •23. Задачи динамического программирования. Общее определение подхода к решению задачи. Пример постановки задачи, решаемой методом динамического программирования.
- •24. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Краскала.
- •25. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Прима.
- •26. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум расстояний до всех вершин графа (узлов сети) – поиск центра графа.
- •27. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум суммы расстояний до всех вершин графа (узлов сети) – поиск медианы графа.
- •28. Кластерный анализ, постановка задачи кластеризации. Алгоритм forel.
- •29. Кластерный анализ, постановка задачи кластеризации. Алгоритм k-средних.
- •30. Надежность сети связи, общие определения. Коэффициент готовности сети связи.
- •31. Надежность простейших сетевых структур. Оценка коэффициента готовности (вероятности исправного состояния) для параллельной и последовательной структур, метод декомпозиции.
- •36. Задачи прогнозирования развития технологий связи (проникновения). Основные характеристики уровня развития. Логистическая модель прогнозирования (логистическая регрессия).
- •38. Пример постановки задачи оптимизации надежности сети связи (максимум надежности).
- •39. Задачи оптимизации. Безусловная оптимизация. Условная оптимизация.
- •40. Экстремумы функций: определения локального и глобального экстремумов.
- •41. Безусловная оптимизация. Необходимые и достаточные условия существования экстремума функции нескольких переменных.
- •42. Условная оптимизация. Метод множителей Лагранжа.
- •43. Условная оптимизация. Условия Каруша-Куна-Таккера.
- •44. Численные методы оптимизации. Общая структура алгоритма. Привести примеры численных методов условной и безусловной оптимизации.
- •45. Оптимизация функции одной переменной. Метод дихотомии.
- •46. Оптимизация функции одной переменной. Метод золотого сечения.
- •47. Оптимизация функции нескольких переменных. Безусловная оптимизация. Покоординатный спуск.
- •48. Оптимизация функции нескольких переменных. Безусловная оптимизация. Симплекс метод Нелдера-Мида (поиск по деформируемому многограннику).
- •49. Оптимизация функции нескольких переменных. Условная оптимизация. Метод штрафных функций.
- •50. Оптимизация функции нескольких переменных. Невыпуклые функции. Эволюционный метод (генетический алгоритм).
47. Оптимизация функции нескольких переменных. Безусловная оптимизация. Покоординатный спуск.
Пусть задана
выпуклая функция
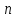 переменных
переменных
 .
.
Данный метод предполагает следующие шаги:
-
Фиксируются все значения переменных кроме одной.
-
Производится поиск экстремума по одной переменной одним из известных методов.
-
Найденное значение присваивается данной переменной и для поиска выбирается следующая переменная.
-
После нахождения экстремумов по каждой из переменных проверяется критерий сходимости. Если условие сходимости не выполняется, то к 1, если выполняется, то полученные значения переменных и принимаются как искомый экстремум.
Данный метод может быть эффективен только при оптимизации относительно простых функций.
|
Пример (из лекции) |
|
|
|
Функция Розенброка
|
|
|
Шаги поиска экстремума (на каждом из шагов используется метод золотого сечения) |
|
Результат:
Вывод: маленькая
точность. Должно быть
Потребовалось около
|
|
48. Оптимизация функции нескольких переменных. Безусловная оптимизация. Симплекс метод Нелдера-Мида (поиск по деформируемому многограннику).
Пусть задана
выпуклая функция
 переменных
переменных
 .
.
Данный метод предполагает следующие шаги:
-
Подготовка. Задается исходный многогранник, содержащий
 вершину (т.е.
вершину (т.е.
 точка – симплекс).
точка – симплекс). -
Оценка. Вычисляются значения функции в вершинах многогранника. Находят «худшую»
 ,
«лучшую»
,
«лучшую»
 ,
и предшествующую «худшей» (по величине)
вершину
,
и предшествующую «худшей» (по величине)
вершину
 .
. -
Отражение. Относительно «наихудшей» точки определяется центр тяжести противоположной грани. Выполняется попытка отражения наихудшей точки через найденный центр тяжести. В результате чего получают точку
 .
. -
Растяжение. Если отраженная точка «лучше» «лучшей», то делается попытка растянуть многогранник в данном направлении. Если растяжение успешное, то полученная точка
 включается в список вершин многогранника,
в противном случае в список вершин
включается отраженная точка
включается в список вершин многогранника,
в противном случае в список вершин
включается отраженная точка
 .
. -
Сокращение. Сокращение производится, если отраженная точка
 хуже точки
хуже точки
 .
Если
.
Если
 лучше
лучше
 ,
то выполняется внешнее сокращение, в
результате которого получают точку
,
то выполняется внешнее сокращение, в
результате которого получают точку
 .
Если
.
Если
 хуже
хуже
 выполняется внутреннее сокращение , в
результате которого получают точку
выполняется внутреннее сокращение , в
результате которого получают точку
 .
Если
.
Если
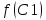 или
или
 ,
то соответствующая точка включается
в список вершин.
,
то соответствующая точка включается
в список вершин. -
Перемещение. Включенная в многогранник точка замещает наихудшую точку
 .
Точка
.
Точка
 исключается, этим достигается перемещение
многогранника.
исключается, этим достигается перемещение
многогранника. -
Сжатие. Сжатие многогранника производится во всех направлениях. При этом лучшая вершина
 остается на месте, а остальные
пересчитываются.
остается на месте, а остальные
пересчитываются. -
Проверка сходимости. Вычисляется среднеквадратическое отклонение значений функции в вершинах многогранника. Если вычисленное значение меньше заданной величины, то сходимость достигнута.
|
Пример (из лекции) |
|
|
|
Функция Розенброка
|
|
|
Шаги поиска экстремума из
точки
|
|
Результат:
Вывод: высокая
точность. Должно быть
Потребовалось всего
|
|
49. Оптимизация функции нескольких переменных. Условная оптимизация. Метод штрафных функций.
Метод заключается в замене исследуемой функции некоторой модифицированной функцией, которая в области допустимых значений близка к исходной функции, а вблизи области ограничений ее значение резко увеличивается.
Задача:
минимизировать функцию
 при ограничениях
при ограничениях
 .
.
Начальный этап.
Выбрать
 в качестве константы остановки, начальную
допустимую точку
в качестве константы остановки, начальную
допустимую точку
 ,
для которой
,
для которой
 ,
скаляр
,
скаляр
 и
и
 .
Положить
.
Положить
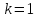 и перейти к основному этапу.
и перейти к основному этапу.
Основной
этап.
 -тая
итерация.
-тая
итерация.
-
При исходной точке
 решить следующую задачу оптимизации:
решить следующую задачу оптимизации:

Минимизировать, где
 – параметр, значение которого убывает
с каждой итерацией
– параметр, значение которого убывает
с каждой итерацией
 при
при
 ,
,
 – положительные весовые коэффициенты,
– положительные весовые коэффициенты,
 .
.
Примерами штрафных функций являются:
-
Обратная функция:
 .
. -
Логарифмическая функция:
 .
.
Положить
 равным оптимальному решению задачи
минимизации и перейти ко второму шагу.
равным оптимальному решению задачи
минимизации и перейти ко второму шагу.
-
Если
 ,
то остановиться. Решение является
искомым.
,
то остановиться. Решение является
искомым.
Иначе положить
 .
Изменить
.
Изменить
 и перейти к первому шагу
и перейти к первому шагу
 -й
итерации.
-й
итерации.
|
Пример (из лекции) |
|
|
|
|
|
Пример на C++ Программа нахождения минимума функции Розенброка. |
|
// C++14 #include <iostream> #include <cmath> #include <functional> #include <algorithm> using namespace std; // Константы: точность и макс. кол-во итераций const double EPS = 1e-8; const int ITERATIONS = 10000; // Функция Розенброка double f(double x, double y) { return (1.0 - x) * (1.0 - x) + 100 * (y - x * x) * (y - x * x); } // Требование 1: x > 3 double psi_1(double x, double y) { return x - 3; } // Требование 2: y > 3 double psi_2(double x, double y) { return y - 3; } // Покоординатный спуск как часть метода штрафных функций void minimize(int k, double &x, double &y, std::function<double(double, double)> &func) { double phi = (1.0 + sqrt(5.0)) / 2.0; // золотое сечение double startX = x - x / (k * phi), stopX = x + x / (k * phi); double startY = y - y / (k * phi), stopY = y + y / (k * phi); for (int i = 0; i < ITERATIONS; ++i) { if (i % 2 == 0) { // оптимизируем X double a = startX, b = stopX; while (fabs(b - a) >= EPS) { double x1 = b - (b - a) / phi, x2 = a + (b - a) / phi; double f1 = func(x1, y), f2 = func(x2, y); a = (f1 >= f2) ? x1 : a; b = (f1 <= f2) ? x2 : b; } x = a + (b - a) / 2.0; } else { // оптимизируем Y double a = startY, b = stopY; while (fabs(b - a) >= EPS) { double y1 = b - (b - a) / phi, y2 = a + (b - a) / phi; double f1 = func(x, y1), f2 = func(x, y2); a = (f1 >= f2) ? y1 : a; b = (f1 <= f2) ? y2 : b; } y = a + (b - a) / 2.0; } } } // Метод штрафных функций int main() { int i = 1; // координаты начальных точек следует устанавливать больше, чем может находится экстремальная точка, например, (20, 20); Экстремальная точка находится f(3, 9) = 4. // значение r устанавливается равным 1 // b в данном случае характеризует приоритет ограничений: чем больше, тем выше вероятность соблюдения ограничений, но 0 < b < 1 double point_x = 20, point_y = 20, r = 1.0, b = 0.7; // Создаем указатель на функцию типа "double func(double, double)". std::function<double(double, double)> func; do { cout << point_x << ' ' << point_y << " -> " << f(point_x, point_y) << endl; // Меняем функцию в соответствии со значением r func = [r] (double x, double y) { return f(x, y) + r / psi_1(x, y) + r / psi_2(x, y); }; // Минимизируем minimize(i, point_x, point_y, func); r *= b; ++i; } while (i < ITERATIONS && func(point_x, point_y) >= EPS); cout << "Result: " << endl; cout << point_x << ' ' << point_y << " -> " << f(point_x, point_y); return 0; }
|
|
20 20 -> 1.44404e+007 7.63932 32.3607 -> 67636.5 5.27864 27.8641 -> 18.3068 4.70318 22.1237 -> 13.715 4.32455 18.7054 -> 11.054 4.04842 16.3933 -> 9.29417 3.83421 14.7047 -> 8.034 3.66101 13.4064 -> 7.08215 3.51673 12.3707 -> 6.33504 3.39381 11.5212 -> 5.7314 3.28726 10.8092 -> 5.23251 3.19359 10.2019 -> 4.81264 3.11036 9.67643 -> 4.45406 3.058 9.35139 -> 4.23538 3.04864 9.29419 -> 4.19691 3.04077 9.24628 -> 4.16474 3.03416 9.20615 -> 4.13782 3.02862 9.17255 -> 4.11531 3.02397 9.14442 -> 4.09647 3.02008 9.12087 -> 4.08071 3.01681 9.10115 -> 4.06753 3.01407 9.08465 -> 4.0565 3.01178 9.07083 -> 4.04727 3.00986 9.05927 -> 4.03955 3.00825 9.0496 -> 4.03309 Result: 3 9 -> 4 |
|
Wolfram
Alpha: |




 .
.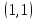 .
. вычислений функции.
вычислений функции.



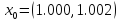 .
. .
. вычислений функции.
вычислений функции.



