- •Математические модели в сетях связи Экзаменационные вопросы и ответы
- •1. Моделирование сетей связи, задачи моделирования, виды моделей. Математические модели сетей связи: назначение, области применения (предметная область).
- •Структура сети связи
- •2. Сеть связи как система массового обслуживания. Основные процессы в сети связи, показатели (параметры) функционирования сети связи.
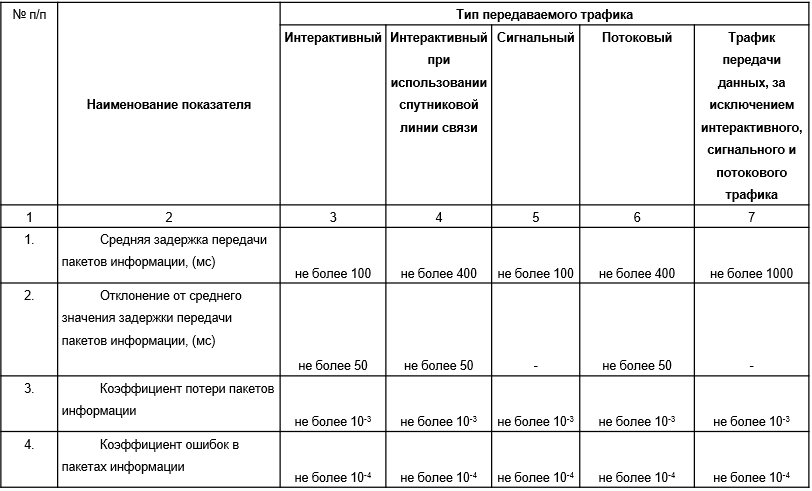
- •3. Показатели качества обслуживания трафика. Понятия потерь (для сетей с кк и кп), задержки доставки данных, вариации задержки (джиттера).
- •4. Обозначения систем массового обслуживания по Кендаллу-Башарину.
- •5. Модель трафика как потока заявок. Понятие случайного потока. Характеристики потока.
- •6. Простейший поток заявок – математическая модель, основные свойства простейшего потока.
- •7. Случайный процесс. Понятие самоподобного трафика, коэффициент Херста, метод оценки коэффициента Херста.
- •8. Понятие абонентской нагрузки. Удельная абонентская нагрузка. Поступающая (производимая), обслуженная, потерянная нагрузка.
- •9. Модель сети с кк как системы массового обслуживания: система м/m/V при дисциплине обслуживания с потерями. Постановка задачи, оценка потерь в сети связи, 1 формула Эрланга.
- •10. Сети с кп. Дисциплины обслуживания заявок (пакетов), модели обслуживания, показатели качества. Система м/m/V (до с ожиданием), 2 формула Эрланга.
- •11. Формула Полячека-Хинчина. Область применения, параметры. Частные случаи для моделей m/m/1 и m/d/1. Время ожидания в очереди, время доставки сообщения (пакета).
- •Свертка:
- •16. Измерения параметров трафика. Объекты измерений, анализируемые параметры, план измерений.
- •Объект измерений:
- •17. Точечные оценки параметров (математическое ожидание и др.).
- •18. Интервальные оценки параметров трафика (доверительные интервалы).
- •19. Гистограммы. Интервалы между пакетами, длина пакетов. Смысловое значение гистограмм. Функции плотности вероятности и функции распределения.
- •20. Имитационное моделирование. Принцип построения дискретных событийных моделей. Упрощенная структура системы моделирования и алгоритм функционирования.
- •21. Получение потока событий с заданными свойствами. Получение случайных чисел с заданной функцией распределения. Метод обратной функции.
- •22. Расчет необходимой пропускной способности канала (линии связи) на примере услуг VoIp.
- •23. Задачи динамического программирования. Общее определение подхода к решению задачи. Пример постановки задачи, решаемой методом динамического программирования.
- •24. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Краскала.
- •25. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Прима.
- •26. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум расстояний до всех вершин графа (узлов сети) – поиск центра графа.
- •27. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум суммы расстояний до всех вершин графа (узлов сети) – поиск медианы графа.
- •28. Кластерный анализ, постановка задачи кластеризации. Алгоритм forel.
- •29. Кластерный анализ, постановка задачи кластеризации. Алгоритм k-средних.
- •30. Надежность сети связи, общие определения. Коэффициент готовности сети связи.
- •31. Надежность простейших сетевых структур. Оценка коэффициента готовности (вероятности исправного состояния) для параллельной и последовательной структур, метод декомпозиции.
- •36. Задачи прогнозирования развития технологий связи (проникновения). Основные характеристики уровня развития. Логистическая модель прогнозирования (логистическая регрессия).
- •38. Пример постановки задачи оптимизации надежности сети связи (максимум надежности).
- •39. Задачи оптимизации. Безусловная оптимизация. Условная оптимизация.
- •40. Экстремумы функций: определения локального и глобального экстремумов.
- •41. Безусловная оптимизация. Необходимые и достаточные условия существования экстремума функции нескольких переменных.
- •42. Условная оптимизация. Метод множителей Лагранжа.
- •43. Условная оптимизация. Условия Каруша-Куна-Таккера.
- •44. Численные методы оптимизации. Общая структура алгоритма. Привести примеры численных методов условной и безусловной оптимизации.
- •45. Оптимизация функции одной переменной. Метод дихотомии.
- •46. Оптимизация функции одной переменной. Метод золотого сечения.
- •47. Оптимизация функции нескольких переменных. Безусловная оптимизация. Покоординатный спуск.
- •48. Оптимизация функции нескольких переменных. Безусловная оптимизация. Симплекс метод Нелдера-Мида (поиск по деформируемому многограннику).
- •49. Оптимизация функции нескольких переменных. Условная оптимизация. Метод штрафных функций.
- •50. Оптимизация функции нескольких переменных. Невыпуклые функции. Эволюционный метод (генетический алгоритм).
1. Моделирование сетей связи, задачи моделирования, виды моделей. Математические модели сетей связи: назначение, области применения (предметная область).
Модель – это описание основных характеристик (качеств и функций) объекта.
Моделирование – способ исследования свойств (получения знаний) об объекте: аналитическое / имитационное.

Любая модель обладает следующими свойствами:
-
Конечностью: модель отображает оригинал лишь в конечном числе его отношений;
-
Упрощенностью: модель отображает только существенные стороны объекта;
-
Приблизительностью: действительность отображается моделью грубо или приблизительно;
-
Адекватностью: модель успешно описывает моделируемую систему;
-
Информативностью: модель должна содержать достаточную информацию о системе в рамках гипотез.
Основная задача моделирования – описание свойств сетей связи и их элементов.
Области применения:
-
Развитие технологий связи и услуг;
-
Качество обслуживания трафика (предоставления услуг);
-
Надежность сети связи (доступность услуг связи);
-
Экономические показатели.
Состав сети связи:
-
Узлы сети (УС)
-
Линии связи (ЛС)


Структура сети связи

|
Разделение каналов |
||
|
Пространственное |
Использование многопарного кабеля |
|
|
Частотное [аналоговый сигнал] |
Канал делится на различные диапазоны полосы пропускания (каналы).
|
|
|
Временное (формирование Импульсно-Кодовой Модуляции) [аналоговый сигнал, цифровой сигнал] |
Разделение времени посредством использования временных интервалов для сигналов
|
|
Специфика сетей связи:
-
Значительные масштабы исследуемой сиcтемы;
-
Изменение свойств системы в процессе развития;
-
Случайные процессы при функционировании;
-
Использование различных технологии реализации услуг…
2. Сеть связи как система массового обслуживания. Основные процессы в сети связи, показатели (параметры) функционирования сети связи.
Сеть связи выполняет работу по обслуживанию трафика. Трафик в сети связи представляет собой процесс поступления и обслуживания заявок пользователей. Процесс поступления заявок, чаще всего, представляет собой случайный процесс. Заявки (вызовы или пакеты данных) поступают в случайные моменты времени. Для обслуживания каждой заявки сеть предоставляет некоторый ресурс, если в момент поступления заявки свободных ресурсов нет, то в зависимости от дисциплины обслуживания, заявка получает либо отказ в обслуживании, либо ставится на ожидание (в очередь).
Сеть связи и ее элементы могут быть представлены как системы массового обслуживания (СМО).
Функционирование СМО характеризуется параметрами трафика, параметрами пропускной способности и параметрами качества обслуживания.
Система массового обслуживания (СМО) – математический (абстрактный) объект, содержащий один или несколько приборов П (каналов), обслуживающих заявки З, поступающие в систему, и накопитель Н, в котором находятся заявки, образующие очередь О и ожидающие обслуживания.
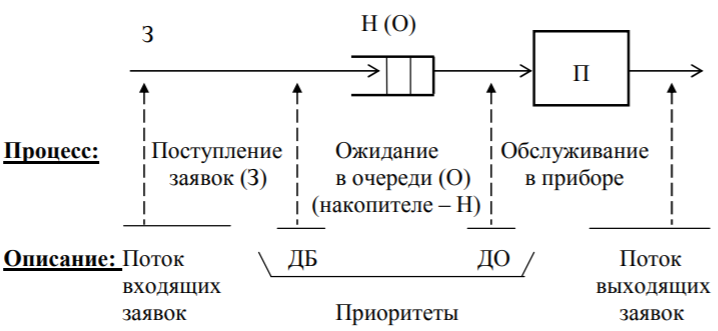
Дисциплина буферизации (ДБ) – правило занесения поступающих заявок в накопитель (буфер).
Дисциплина обслуживания (ДО) – правило выбора заявок из очереди для обслуживания в приборе.
Основная задача моделирования сети связи – определить соотношение между трафиком, ресурсами сети и качеством обслуживания QoS (Quality of Service).

|
Параметры функционирования и параметры надежности |
|
|
|
|
|
|
|