
- •Математические модели в сетях связи Экзаменационные вопросы и ответы
- •1. Моделирование сетей связи, задачи моделирования, виды моделей. Математические модели сетей связи: назначение, области применения (предметная область).
- •Структура сети связи
- •2. Сеть связи как система массового обслуживания. Основные процессы в сети связи, показатели (параметры) функционирования сети связи.
- •3. Показатели качества обслуживания трафика. Понятия потерь (для сетей с кк и кп), задержки доставки данных, вариации задержки (джиттера).
- •4. Обозначения систем массового обслуживания по Кендаллу-Башарину.
- •5. Модель трафика как потока заявок. Понятие случайного потока. Характеристики потока.
- •6. Простейший поток заявок – математическая модель, основные свойства простейшего потока.
- •7. Случайный процесс. Понятие самоподобного трафика, коэффициент Херста, метод оценки коэффициента Херста.
- •8. Понятие абонентской нагрузки. Удельная абонентская нагрузка. Поступающая (производимая), обслуженная, потерянная нагрузка.
- •9. Модель сети с кк как системы массового обслуживания: система м/m/V при дисциплине обслуживания с потерями. Постановка задачи, оценка потерь в сети связи, 1 формула Эрланга.
- •10. Сети с кп. Дисциплины обслуживания заявок (пакетов), модели обслуживания, показатели качества. Система м/m/V (до с ожиданием), 2 формула Эрланга.
- •11. Формула Полячека-Хинчина. Область применения, параметры. Частные случаи для моделей m/m/1 и m/d/1. Время ожидания в очереди, время доставки сообщения (пакета).
- •Свертка:
- •16. Измерения параметров трафика. Объекты измерений, анализируемые параметры, план измерений.
- •Объект измерений:
- •17. Точечные оценки параметров (математическое ожидание и др.).
- •18. Интервальные оценки параметров трафика (доверительные интервалы).
- •19. Гистограммы. Интервалы между пакетами, длина пакетов. Смысловое значение гистограмм. Функции плотности вероятности и функции распределения.
- •20. Имитационное моделирование. Принцип построения дискретных событийных моделей. Упрощенная структура системы моделирования и алгоритм функционирования.
- •21. Получение потока событий с заданными свойствами. Получение случайных чисел с заданной функцией распределения. Метод обратной функции.
- •22. Расчет необходимой пропускной способности канала (линии связи) на примере услуг VoIp.
- •23. Задачи динамического программирования. Общее определение подхода к решению задачи. Пример постановки задачи, решаемой методом динамического программирования.
- •24. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Краскала.
- •25. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Прима.
- •26. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум расстояний до всех вершин графа (узлов сети) – поиск центра графа.
- •27. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум суммы расстояний до всех вершин графа (узлов сети) – поиск медианы графа.
- •28. Кластерный анализ, постановка задачи кластеризации. Алгоритм forel.
- •29. Кластерный анализ, постановка задачи кластеризации. Алгоритм k-средних.
- •30. Надежность сети связи, общие определения. Коэффициент готовности сети связи.
- •31. Надежность простейших сетевых структур. Оценка коэффициента готовности (вероятности исправного состояния) для параллельной и последовательной структур, метод декомпозиции.
- •36. Задачи прогнозирования развития технологий связи (проникновения). Основные характеристики уровня развития. Логистическая модель прогнозирования (логистическая регрессия).
- •38. Пример постановки задачи оптимизации надежности сети связи (максимум надежности).
- •39. Задачи оптимизации. Безусловная оптимизация. Условная оптимизация.
- •40. Экстремумы функций: определения локального и глобального экстремумов.
- •41. Безусловная оптимизация. Необходимые и достаточные условия существования экстремума функции нескольких переменных.
- •42. Условная оптимизация. Метод множителей Лагранжа.
- •43. Условная оптимизация. Условия Каруша-Куна-Таккера.
- •44. Численные методы оптимизации. Общая структура алгоритма. Привести примеры численных методов условной и безусловной оптимизации.
- •45. Оптимизация функции одной переменной. Метод дихотомии.
- •46. Оптимизация функции одной переменной. Метод золотого сечения.
- •47. Оптимизация функции нескольких переменных. Безусловная оптимизация. Покоординатный спуск.
- •48. Оптимизация функции нескольких переменных. Безусловная оптимизация. Симплекс метод Нелдера-Мида (поиск по деформируемому многограннику).
- •49. Оптимизация функции нескольких переменных. Условная оптимизация. Метод штрафных функций.
- •50. Оптимизация функции нескольких переменных. Невыпуклые функции. Эволюционный метод (генетический алгоритм).
40. Экстремумы функций: определения локального и глобального экстремумов.
Экстремум — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Стационарная точка — точка, в которой значение производной функции равно 0.
Критическая
точка — точка, в которой значение
производной функции равно 0 (стационарная
точка) или не существует (например,
 при
при
 – минимум, но производной в этой точке
не существует).
– минимум, но производной в этой точке
не существует).
Теорема
Ферма (необходимый признак существования
экстремума функции). Если точка
 – точка экстремума функции
– точка экстремума функции
 ,
то в этой точке производная функции
равна нулю (
,
то в этой точке производная функции
равна нулю ( )
или не существует.
)
или не существует.
Теорема
(первый достаточный признак существования
экстремума функции). Критическая
точка
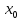 является точкой экстремума функции
является точкой экстремума функции
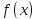 ,
если при переходе через эту точку
производная функции меняет знак, причём,
если знак меняется с "плюса" на
"минус", то точкой максимума, а если
с "минуса" на "плюс", то точкой
минимума.
,
если при переходе через эту точку
производная функции меняет знак, причём,
если знак меняется с "плюса" на
"минус", то точкой максимума, а если
с "минуса" на "плюс", то точкой
минимума.
Теорема
(второй достаточный признак существования
экстремума функции). Критическая
точка
 является точкой экстремума функции
является точкой экстремума функции
 ,
если
,
если
 дважды дифференцируема в точке
дважды дифференцируема в точке
 и
и
 .
Причём, если вторая производная меньше
нуля (
.
Причём, если вторая производная меньше
нуля ( ),
то
),
то
 – точка максимума, а если вторая
производная больше нуля (
– точка максимума, а если вторая
производная больше нуля ( ),
то
),
то
 – точка минимума.
– точка минимума.
|
|
Функция (синяя) и её производная (красная). Глобальный максимум функции — «звездочка» Глобальный минимум — «квадрат». Локальный максимум — «ромб». Локальный минимум — «плюс». Нуль производной без экстремума – «крест». Видно, что остальные нули производной соответствуют точкам экстремума функции. |
|
Пусть дана функция
Тогда
Т. е. если значение функции в этой точке больше значений функции в достаточно близких к ней точках, расположенных справа и слева от неё.
Т. е. если значение функции в этой точке меньше значений функции в достаточно близких к ней точках, расположенных справа и слева от неё.
|
|
41. Безусловная оптимизация. Необходимые и достаточные условия существования экстремума функции нескольких переменных.
|
Необходимое и достаточное условия существования экстремума функции нескольких переменных |
|||||||||
|
Пусть задана
функция нескольких
Необходимое условие существования локального экстремума В точке
Если условия
выполняются, то точка
Достаточное условие существования локального экстремума Теорема 1.
Если в точке
Если вторая
производная функции в точке
Теорема 2.
Если функция одной переменной имеет
в точке
Для анализа поведения функции в точке потребуются некоторые свойства квадратичных функций. Квадратичная функция (форма):
Если квадратичная форма:
Определитель Гессе (Гессиан):
Собственные значения можно найти как корни уравнения:
Теорема3.
Пусть для функции
Тогда:
|
|||||||||
|
Пример №1 Исследовать
на экстремум функцию
Вычислим частные производные первого порядка:
Составляем систему:
Находим два
решения – две стационарные точки:
Находим частные производные второго порядка:
Находим определитель Гессе:
При
При
Находим собственные значения и определяем тип экстремума:
Собственные значения
положительны. Точка
|
|||||||||
|
Пример №2 Исследовать
на экстремум функцию
Вычислим частные производные первого порядка:
Составляем систему:
Находим девять
решений – девять стационарных точек:
Находим частные производные второго порядка:
Находим определитель Гессе:
Находим собственные значения и определяем типы экстремумов:
Подставляя
координаты точек в последнее уравнение
|


 и
и
 — внутренняя точка области определения
— внутренняя точка области определения
 .
. :
: .
. .
. .
. .
. переменных
переменных
 .
.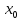 имеет место экстремум тогда, когда
она дифференцируема в данной точке и
все частные производные функции в
этой точке равны нулю.
имеет место экстремум тогда, когда
она дифференцируема в данной точке и
все частные производные функции в
этой точке равны нулю.
 называется стационарной точкой.
называется стационарной точкой. первая производная функции равна нулю
первая производная функции равна нулю
 ,
а вторая производная
,
а вторая производная
 ,
то функция в точке
,
то функция в точке
 имеет локальный минимум, если
имеет локальный минимум, если
 ,
то локальный максимум.
,
то локальный максимум. равна
нулю, то необходимо исследовать
производные высших порядков в
соответствии со следующей теоремой.
равна
нулю, то необходимо исследовать
производные высших порядков в
соответствии со следующей теоремой.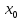 производные до
производные до
 порядка равными нулю и производная
порядка равными нулю и производная
 ,
то тогда точка
,
то тогда точка
 :
:

 ,
то в точке
,
то в точке
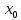 имеет место максимум.
имеет место максимум. ,
то в точке
,
то в точке
 имеет место минимум.
имеет место минимум.
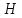 отрицательны. Имеет место максимум.
отрицательны. Имеет место максимум.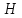 положительны. Имеет место минимум.
положительны. Имеет место минимум. имеют разные знаки, то экстремума в
данной точке нет.
имеют разные знаки, то экстремума в
данной точке нет.
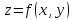 в окрестности точки
в окрестности точки
 выполняются условия:
выполняются условия: и
и
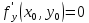 .
.
 ,
то функция
,
то функция
 в точке
в точке
 не имеет экстремума.
не имеет экстремума. ,
то функция
,
то функция
 в точке
в точке
 может иметь или не иметь экстремума
(нужны дополнительные исследования).
может иметь или не иметь экстремума
(нужны дополнительные исследования). ,
то функция
,
то функция
 в точке
в точке
 имеет экстремум.
имеет экстремум.
 .
.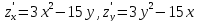
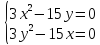
 и
и
 .
.
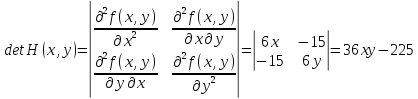
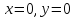 :
:
 .
Экстремума нет.
.
Экстремума нет. :
:
 .
Экстремум есть.
.
Экстремум есть.

 – точка минимума.
– точка минимума.
 .
.
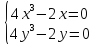
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.

 :
:
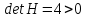 .
Экстремум +
.
Экстремум +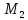 :
:

 :
:

 :
:

 :
:
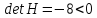
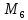 :
:
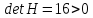 .
Экстремум +
.
Экстремум + :
:
 .
Экстремум +
.
Экстремум + :
:
 .
Экстремум +
.
Экстремум + :
:
 .
Экстремум +
.
Экстремум +
 ,
получим:
,
получим: :
:
 .
Точка максимума.
.
Точка максимума. :
:
 .
Точки минимума.
.
Точки минимума.