
- •Математические модели в сетях связи Экзаменационные вопросы и ответы
- •1. Моделирование сетей связи, задачи моделирования, виды моделей. Математические модели сетей связи: назначение, области применения (предметная область).
- •Структура сети связи
- •2. Сеть связи как система массового обслуживания. Основные процессы в сети связи, показатели (параметры) функционирования сети связи.
- •3. Показатели качества обслуживания трафика. Понятия потерь (для сетей с кк и кп), задержки доставки данных, вариации задержки (джиттера).
- •4. Обозначения систем массового обслуживания по Кендаллу-Башарину.
- •5. Модель трафика как потока заявок. Понятие случайного потока. Характеристики потока.
- •6. Простейший поток заявок – математическая модель, основные свойства простейшего потока.
- •7. Случайный процесс. Понятие самоподобного трафика, коэффициент Херста, метод оценки коэффициента Херста.
- •8. Понятие абонентской нагрузки. Удельная абонентская нагрузка. Поступающая (производимая), обслуженная, потерянная нагрузка.
- •9. Модель сети с кк как системы массового обслуживания: система м/m/V при дисциплине обслуживания с потерями. Постановка задачи, оценка потерь в сети связи, 1 формула Эрланга.
- •10. Сети с кп. Дисциплины обслуживания заявок (пакетов), модели обслуживания, показатели качества. Система м/m/V (до с ожиданием), 2 формула Эрланга.
- •11. Формула Полячека-Хинчина. Область применения, параметры. Частные случаи для моделей m/m/1 и m/d/1. Время ожидания в очереди, время доставки сообщения (пакета).
- •Свертка:
- •16. Измерения параметров трафика. Объекты измерений, анализируемые параметры, план измерений.
- •Объект измерений:
- •17. Точечные оценки параметров (математическое ожидание и др.).
- •18. Интервальные оценки параметров трафика (доверительные интервалы).
- •19. Гистограммы. Интервалы между пакетами, длина пакетов. Смысловое значение гистограмм. Функции плотности вероятности и функции распределения.
- •20. Имитационное моделирование. Принцип построения дискретных событийных моделей. Упрощенная структура системы моделирования и алгоритм функционирования.
- •21. Получение потока событий с заданными свойствами. Получение случайных чисел с заданной функцией распределения. Метод обратной функции.
- •22. Расчет необходимой пропускной способности канала (линии связи) на примере услуг VoIp.
- •23. Задачи динамического программирования. Общее определение подхода к решению задачи. Пример постановки задачи, решаемой методом динамического программирования.
- •24. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Краскала.
- •25. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Прима.
- •26. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум расстояний до всех вершин графа (узлов сети) – поиск центра графа.
- •27. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум суммы расстояний до всех вершин графа (узлов сети) – поиск медианы графа.
- •28. Кластерный анализ, постановка задачи кластеризации. Алгоритм forel.
- •29. Кластерный анализ, постановка задачи кластеризации. Алгоритм k-средних.
- •30. Надежность сети связи, общие определения. Коэффициент готовности сети связи.
- •31. Надежность простейших сетевых структур. Оценка коэффициента готовности (вероятности исправного состояния) для параллельной и последовательной структур, метод декомпозиции.
- •36. Задачи прогнозирования развития технологий связи (проникновения). Основные характеристики уровня развития. Логистическая модель прогнозирования (логистическая регрессия).
- •38. Пример постановки задачи оптимизации надежности сети связи (максимум надежности).
- •39. Задачи оптимизации. Безусловная оптимизация. Условная оптимизация.
- •40. Экстремумы функций: определения локального и глобального экстремумов.
- •41. Безусловная оптимизация. Необходимые и достаточные условия существования экстремума функции нескольких переменных.
- •42. Условная оптимизация. Метод множителей Лагранжа.
- •43. Условная оптимизация. Условия Каруша-Куна-Таккера.
- •44. Численные методы оптимизации. Общая структура алгоритма. Привести примеры численных методов условной и безусловной оптимизации.
- •45. Оптимизация функции одной переменной. Метод дихотомии.
- •46. Оптимизация функции одной переменной. Метод золотого сечения.
- •47. Оптимизация функции нескольких переменных. Безусловная оптимизация. Покоординатный спуск.
- •48. Оптимизация функции нескольких переменных. Безусловная оптимизация. Симплекс метод Нелдера-Мида (поиск по деформируемому многограннику).
- •49. Оптимизация функции нескольких переменных. Условная оптимизация. Метод штрафных функций.
- •50. Оптимизация функции нескольких переменных. Невыпуклые функции. Эволюционный метод (генетический алгоритм).
38. Пример постановки задачи оптимизации надежности сети связи (максимум надежности).
|
Надежность сети связи |
Рассматривается
сеть связи с коммутацией каналов (КК).
Структура сети задана графом. Сеть
состоит из
Выберем в качестве целевого показателя средневзвешенную вероятность исправного состояния сети
Целевая функция
|
39. Задачи оптимизации. Безусловная оптимизация. Условная оптимизация.
Оптимизация — процесс нахождения экстремума (глобального максимума или минимума) определённой функции или выбора наилучшего (оптимального) варианта из множества возможных. Наиболее надёжным способом нахождения наилучшего варианта является сравнительная оценка всех возможных вариантов (альтернатив). Если число альтернатив велико, при поиске наилучшей обычно используют методы математического программирования. Применить эти методы можно, если есть строгая постановка задачи: задан набор переменных, установлена область их возможного изменения (заданы ограничения) и определён вид целевой функции (функции, экстремум которой нужно найти) от этих переменных. Последняя представляет собой количественную меру (критерий) оценки степени достижения поставленной цели.
Выбор оптимального решения или сравнение двух альтернативных решений проводится с помощью некоторой зависимой величины, которая называется целевой функцией (или критерием качества). В процессе решения задачи оптимизации должны быть найдены такие значения параметров, при которых целевая функция имеет минимум (или максимум).
Задача безусловной оптимизации (задача не имеет ограничений) состоит в нахождении минимума или максимума функции в отсутствие каких-либо ограничений. Многие алгоритмы решения задачи с ограничениями предполагают сведение ее к последовательности задач безусловной оптимизации. Другой класс методов основан на поиске подходящего направления и последующей минимизации вдоль этого направления.
Задача
условной оптимизации (задача имеет
ограничения) заключается в поиске
минимального или максимального значения
скалярной функции
 .
Решение задачи основывается на линейной
или квадратичной аппроксимации целевой
функции для определения приращений
.
Решение задачи основывается на линейной
или квадратичной аппроксимации целевой
функции для определения приращений
 на каждой итерации. Существуют также
приближенные методы решения нелинейных
задач, основанные на методе кусочно-линейной
аппроксимации.
на каждой итерации. Существуют также
приближенные методы решения нелинейных
задач, основанные на методе кусочно-линейной
аппроксимации.
Аналитические методы оптимизации:
-
Безусловная оптимизация (необходимые и достаточные условия существования экстремума функции).
-
Условная оптимизация (метод множителей Лагранжа, условия Каруша-Куна-Таккера).

 узлов связи и
узлов связи и
 направлений связи (ребер графа).
направлений связи (ребер графа).
 — число каналов в
— число каналов в
 направлений связи
направлений связи — надежность канала в
— надежность канала в
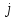 направлений связи (вероятность
исправного состояния)
направлений связи (вероятность
исправного состояния) — значимость
— значимость
 направления связи,
направления связи,

 — общее число каналов в сети
— общее число каналов в сети
 .
. .
.
