- •Математические модели в сетях связи Экзаменационные вопросы и ответы
- •1. Моделирование сетей связи, задачи моделирования, виды моделей. Математические модели сетей связи: назначение, области применения (предметная область).
- •Структура сети связи
- •2. Сеть связи как система массового обслуживания. Основные процессы в сети связи, показатели (параметры) функционирования сети связи.
- •3. Показатели качества обслуживания трафика. Понятия потерь (для сетей с кк и кп), задержки доставки данных, вариации задержки (джиттера).
- •4. Обозначения систем массового обслуживания по Кендаллу-Башарину.
- •5. Модель трафика как потока заявок. Понятие случайного потока. Характеристики потока.
- •6. Простейший поток заявок – математическая модель, основные свойства простейшего потока.
- •7. Случайный процесс. Понятие самоподобного трафика, коэффициент Херста, метод оценки коэффициента Херста.
- •8. Понятие абонентской нагрузки. Удельная абонентская нагрузка. Поступающая (производимая), обслуженная, потерянная нагрузка.
- •9. Модель сети с кк как системы массового обслуживания: система м/m/V при дисциплине обслуживания с потерями. Постановка задачи, оценка потерь в сети связи, 1 формула Эрланга.
- •10. Сети с кп. Дисциплины обслуживания заявок (пакетов), модели обслуживания, показатели качества. Система м/m/V (до с ожиданием), 2 формула Эрланга.
- •11. Формула Полячека-Хинчина. Область применения, параметры. Частные случаи для моделей m/m/1 и m/d/1. Время ожидания в очереди, время доставки сообщения (пакета).
- •Свертка:
- •16. Измерения параметров трафика. Объекты измерений, анализируемые параметры, план измерений.
- •Объект измерений:
- •17. Точечные оценки параметров (математическое ожидание и др.).
- •18. Интервальные оценки параметров трафика (доверительные интервалы).
- •19. Гистограммы. Интервалы между пакетами, длина пакетов. Смысловое значение гистограмм. Функции плотности вероятности и функции распределения.
- •20. Имитационное моделирование. Принцип построения дискретных событийных моделей. Упрощенная структура системы моделирования и алгоритм функционирования.
- •21. Получение потока событий с заданными свойствами. Получение случайных чисел с заданной функцией распределения. Метод обратной функции.
- •22. Расчет необходимой пропускной способности канала (линии связи) на примере услуг VoIp.
- •23. Задачи динамического программирования. Общее определение подхода к решению задачи. Пример постановки задачи, решаемой методом динамического программирования.
- •24. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Краскала.
- •25. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Прима.
- •26. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум расстояний до всех вершин графа (узлов сети) – поиск центра графа.
- •27. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум суммы расстояний до всех вершин графа (узлов сети) – поиск медианы графа.
- •28. Кластерный анализ, постановка задачи кластеризации. Алгоритм forel.
- •29. Кластерный анализ, постановка задачи кластеризации. Алгоритм k-средних.
- •30. Надежность сети связи, общие определения. Коэффициент готовности сети связи.
- •31. Надежность простейших сетевых структур. Оценка коэффициента готовности (вероятности исправного состояния) для параллельной и последовательной структур, метод декомпозиции.
- •36. Задачи прогнозирования развития технологий связи (проникновения). Основные характеристики уровня развития. Логистическая модель прогнозирования (логистическая регрессия).
- •38. Пример постановки задачи оптимизации надежности сети связи (максимум надежности).
- •39. Задачи оптимизации. Безусловная оптимизация. Условная оптимизация.
- •40. Экстремумы функций: определения локального и глобального экстремумов.
- •41. Безусловная оптимизация. Необходимые и достаточные условия существования экстремума функции нескольких переменных.
- •42. Условная оптимизация. Метод множителей Лагранжа.
- •43. Условная оптимизация. Условия Каруша-Куна-Таккера.
- •44. Численные методы оптимизации. Общая структура алгоритма. Привести примеры численных методов условной и безусловной оптимизации.
- •45. Оптимизация функции одной переменной. Метод дихотомии.
- •46. Оптимизация функции одной переменной. Метод золотого сечения.
- •47. Оптимизация функции нескольких переменных. Безусловная оптимизация. Покоординатный спуск.
- •48. Оптимизация функции нескольких переменных. Безусловная оптимизация. Симплекс метод Нелдера-Мида (поиск по деформируемому многограннику).
- •49. Оптимизация функции нескольких переменных. Условная оптимизация. Метод штрафных функций.
- •50. Оптимизация функции нескольких переменных. Невыпуклые функции. Эволюционный метод (генетический алгоритм).
31. Надежность простейших сетевых структур. Оценка коэффициента готовности (вероятности исправного состояния) для параллельной и последовательной структур, метод декомпозиции.
|
Тип |
Расчет |
Иллюстрация |
|
Надежность последовательной простейшей структуры |
|
|
|
Надежность параллельной простейшей структуры |
|
|
Декомпозиция, как процесс расчленения, позволяет рассматривать любую исследуемую систему как сложную, состоящую из отдельных взаимосвязанных подсистем, которые, в свою очередь, также могут быть расчленены на части.
В общей теории систем доказано, что большинство систем могут быть декомпозированы на базовые представления подсистем. К ним относят:
-
Последовательное соединение элементов,
-
Параллельное соединение элементов,
-
Соединение с помощью обратной связи.
|
Пример |
||
|
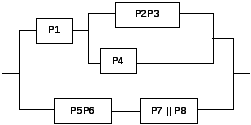
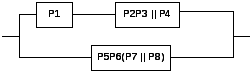
Исходная структура |
Действие |
Результирующая структура |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
32. Оценка коэффициента готовности (вероятности исправного состояния) для мостовой структуры.
|
|
|
|
|
|
|
|
|
|
|
|
33. Оценка коэффициента готовности (вероятности исправного состояния) для структуры общего вида. Метод включения-исключения.
Пусть граф
сети имеет
 путей между заданными двумя узлами.
путей между заданными двумя узлами.
 — событие, означающее исправность всех
элементов пути
— событие, означающее исправность всех
элементов пути
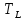 .
.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
34. Поиск самого надежного пути в сети. Постановка задачи, весовые коэффициенты ребер графа.
|
Граф |
Самый надежный путь |
|
|
Трехместная операция, в алгоритме Флойда-Уоршалла
|
35. Задачи прогнозирования развития технологий связи (проникновения). Основные характеристики уровня развития. Линейная модель прогнозирования (линейная регрессия).
Основными
показателями развития технологий
телекоммуникаций являются степень и
динамика их распространения. Обычно,
этот показатель оценивается проникновением
той или иной технологии, т.е. числом
пользователей на 100 жителей. Динамика
изменения проникновения характеризуется
некоторой функцией
 ,
определяющей зависимость проникновения
от времени. Для построения этой зависимости
применяются методы аппроксимации
исходных данных
,
определяющей зависимость проникновения
от времени. Для построения этой зависимости
применяются методы аппроксимации
исходных данных
 (временного ряда) некоторой функцией.
Для этой цели может быть использован,
например, метод наименьших квадратов
или другие методы выбора параметров
функции
(временного ряда) некоторой функцией.
Для этой цели может быть использован,
например, метод наименьших квадратов
или другие методы выбора параметров
функции
 путем минимизации отклонений ее значений,
от значений определяемых исходным рядом
путем минимизации отклонений ее значений,
от значений определяемых исходным рядом
 .
.
Существенную роль при построении прогноза имеет выбор аппроксимирующей функции. Основным требованием к данной функции является непрерывность на интервале прогнозирования. Однако выполнения этого требования не достаточно для получения адекватного прогноза. Понятно, что выбираемая функция, по возможности, должна наилучшим образом, отражать процесс изменения прогнозируемой величины. Поэтому, при выборе функции следует руководствоваться знаниями об исследуемом процессе и подобных процессах, возможно в других областях знаний, т.е. использовать ассоциативный подход.
Практически, при построении краткосрочных прогнозов, часто используется линейная регрессия.
|
Линейная регрессия |
|
|
Линейная регрессия |
Линейная регрессия с доверительным интервалом |
|
Доверительный
интервал для прогнозируемых значений
В этом случае предполагается, что имеет место линейная тенденция изменения прогнозируемой величины, а также сохраняется случайный характер ее изменения, поэтому результатом прогноза является доверительный интервал. Ширина доверительного интервала расширяется с увеличением интервала прогнозирования, а ее минимальное значение приходится на середину интервала исходных данных. |
|












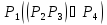





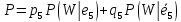







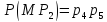







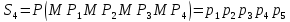




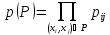




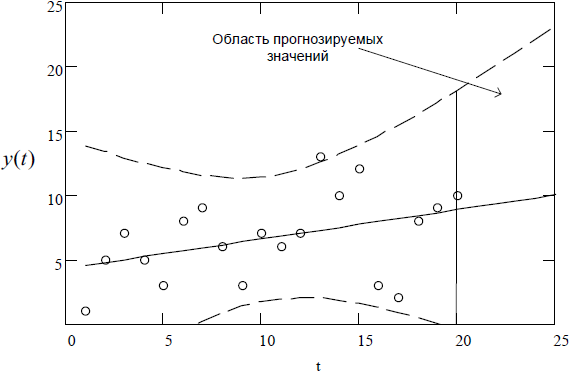
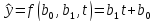



 будет определяться как:
будет определяться как: