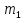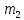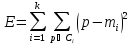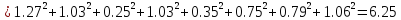- •Математические модели в сетях связи Экзаменационные вопросы и ответы
- •1. Моделирование сетей связи, задачи моделирования, виды моделей. Математические модели сетей связи: назначение, области применения (предметная область).
- •Структура сети связи
- •2. Сеть связи как система массового обслуживания. Основные процессы в сети связи, показатели (параметры) функционирования сети связи.
- •3. Показатели качества обслуживания трафика. Понятия потерь (для сетей с кк и кп), задержки доставки данных, вариации задержки (джиттера).
- •4. Обозначения систем массового обслуживания по Кендаллу-Башарину.
- •5. Модель трафика как потока заявок. Понятие случайного потока. Характеристики потока.
- •6. Простейший поток заявок – математическая модель, основные свойства простейшего потока.
- •7. Случайный процесс. Понятие самоподобного трафика, коэффициент Херста, метод оценки коэффициента Херста.
- •8. Понятие абонентской нагрузки. Удельная абонентская нагрузка. Поступающая (производимая), обслуженная, потерянная нагрузка.
- •9. Модель сети с кк как системы массового обслуживания: система м/m/V при дисциплине обслуживания с потерями. Постановка задачи, оценка потерь в сети связи, 1 формула Эрланга.
- •10. Сети с кп. Дисциплины обслуживания заявок (пакетов), модели обслуживания, показатели качества. Система м/m/V (до с ожиданием), 2 формула Эрланга.
- •11. Формула Полячека-Хинчина. Область применения, параметры. Частные случаи для моделей m/m/1 и m/d/1. Время ожидания в очереди, время доставки сообщения (пакета).
- •Свертка:
- •16. Измерения параметров трафика. Объекты измерений, анализируемые параметры, план измерений.
- •Объект измерений:
- •17. Точечные оценки параметров (математическое ожидание и др.).
- •18. Интервальные оценки параметров трафика (доверительные интервалы).
- •19. Гистограммы. Интервалы между пакетами, длина пакетов. Смысловое значение гистограмм. Функции плотности вероятности и функции распределения.
- •20. Имитационное моделирование. Принцип построения дискретных событийных моделей. Упрощенная структура системы моделирования и алгоритм функционирования.
- •21. Получение потока событий с заданными свойствами. Получение случайных чисел с заданной функцией распределения. Метод обратной функции.
- •22. Расчет необходимой пропускной способности канала (линии связи) на примере услуг VoIp.
- •23. Задачи динамического программирования. Общее определение подхода к решению задачи. Пример постановки задачи, решаемой методом динамического программирования.
- •24. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Краскала.
- •25. Постановка задачи выбора оптимальной структуры сети (минимальной протяженности линий). Алгоритмы поиска кратчайшего остова графа. Алгоритм Прима.
- •26. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум расстояний до всех вершин графа (узлов сети) – поиск центра графа.
- •27. Постановка задачи оптимального размещения оборудования в сети, заданной графом. Минимум суммы расстояний до всех вершин графа (узлов сети) – поиск медианы графа.
- •28. Кластерный анализ, постановка задачи кластеризации. Алгоритм forel.
- •29. Кластерный анализ, постановка задачи кластеризации. Алгоритм k-средних.
- •30. Надежность сети связи, общие определения. Коэффициент готовности сети связи.
- •31. Надежность простейших сетевых структур. Оценка коэффициента готовности (вероятности исправного состояния) для параллельной и последовательной структур, метод декомпозиции.
- •36. Задачи прогнозирования развития технологий связи (проникновения). Основные характеристики уровня развития. Логистическая модель прогнозирования (логистическая регрессия).
- •38. Пример постановки задачи оптимизации надежности сети связи (максимум надежности).
- •39. Задачи оптимизации. Безусловная оптимизация. Условная оптимизация.
- •40. Экстремумы функций: определения локального и глобального экстремумов.
- •41. Безусловная оптимизация. Необходимые и достаточные условия существования экстремума функции нескольких переменных.
- •42. Условная оптимизация. Метод множителей Лагранжа.
- •43. Условная оптимизация. Условия Каруша-Куна-Таккера.
- •44. Численные методы оптимизации. Общая структура алгоритма. Привести примеры численных методов условной и безусловной оптимизации.
- •45. Оптимизация функции одной переменной. Метод дихотомии.
- •46. Оптимизация функции одной переменной. Метод золотого сечения.
- •47. Оптимизация функции нескольких переменных. Безусловная оптимизация. Покоординатный спуск.
- •48. Оптимизация функции нескольких переменных. Безусловная оптимизация. Симплекс метод Нелдера-Мида (поиск по деформируемому многограннику).
- •49. Оптимизация функции нескольких переменных. Условная оптимизация. Метод штрафных функций.
- •50. Оптимизация функции нескольких переменных. Невыпуклые функции. Эволюционный метод (генетический алгоритм).
29. Кластерный анализ, постановка задачи кластеризации. Алгоритм k-средних.
Метод
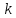 -средних
(англ. k-means) — наиболее популярный
метод кластеризации.
-средних
(англ. k-means) — наиболее популярный
метод кластеризации.
Действие алгоритма таково, что он стремится минимизировать суммарное квадратичное отклонение точек кластеров от центров этих кластеров.
|
Метод
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Изображение |
Описание |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Шаг 1. Определим
число кластеров, на которое требуется
разбить исходное множество
Шаг 2. Случайным образом выберем
две точки, которые будут начальными
центрами кластеров. Пусть это будут
точки
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Шаг 3. Проход 1. Для каждой точки определим к ней ближайший центр кластера с помощью расстояния Евклида. В таблице представлены вычисленные с помощью формулы
расстояния
между центрами кластеров
Таким
образом, кластер 1 содержит точки A,
E, G, а кластер 2 – точки B,
C, D, F, H. Как только
определятся члены кластеров, может
быть рассчитана сумма квадратичных
ошибок (
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
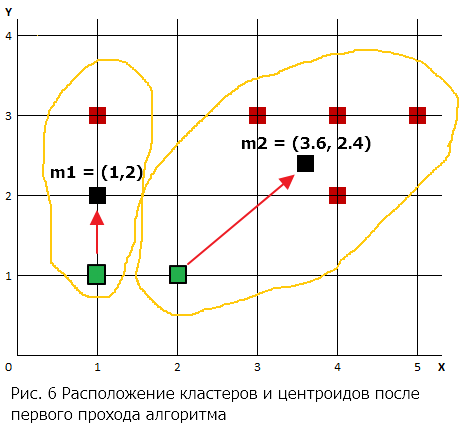
Шаг 4. Проход 1. Для каждого кластера вычисляется его центроид, и центр кластера перемещается в него. Центроид
для кластера 1:
Центроид
для кластера 2:
Начальные центры кластеров закрашены зеленым цветом, а центроиды, вычисленные при 1-м проходе алгоритма, – закрашены черным цветом. Они и будут являться новыми центрами кластеров, к которым будет определяться принадлежность точек данных на втором проходе. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Шаг 3. Проход 2. После того, как найдены новые центры кластеров, для каждой точки снова определяется ближайший к ней центр и ее отношение к соответствующему кластеру. Для это еще раз вычисляются евклидовы расстояния между точками и центрами кластеров. Относительно
большое изменение
Результат показывает уменьшение ошибки относительно начального состояния центров кластеров (которая на первом проходе составляла 36). Это говорит об улучшении качества кластеризации, т.е. более высокую «кучность» объектов относительно центра кластера. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
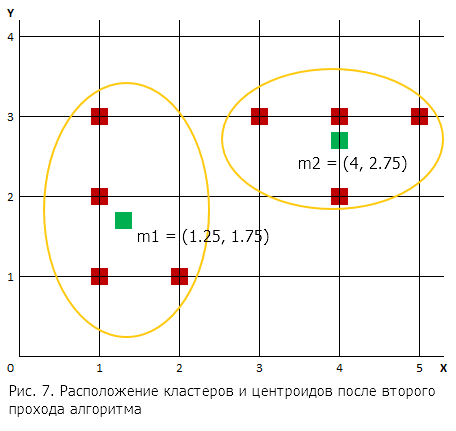
Шаг 4. Проход 2. Для каждого кластера вновь вычисляется его центроид, и центр кластера перемещается в него. Новый центроид для 1-го кластера:
Центроид для кластера 2:
Расположение кластеров и центроидов после второго прохода алгоритма представлено на рисунке. По сравнению с предыдущим проходом центры кластеров изменились незначительно. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Шаг 3. Проход 3. Для каждой записи вновь ищется ближайший к ней центр кластера. Следует отметить, что записей, сменивших кластер на данном проходе алгоритма, не было. Новая сумма квадратов ошибок составит:
Таким образом, изменение суммы квадратов ошибок является незначительным по сравнению с предыдущим проходом. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Шаг 4. Проход 3. Для каждого кластера вновь вычисляется его центроид, и центр кластера перемещается в него. Но поскольку на данном проходе ни одна запись не изменила своего членства в кластерах, то положение центроида не поменялось, и алгоритм завершает свою работу. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
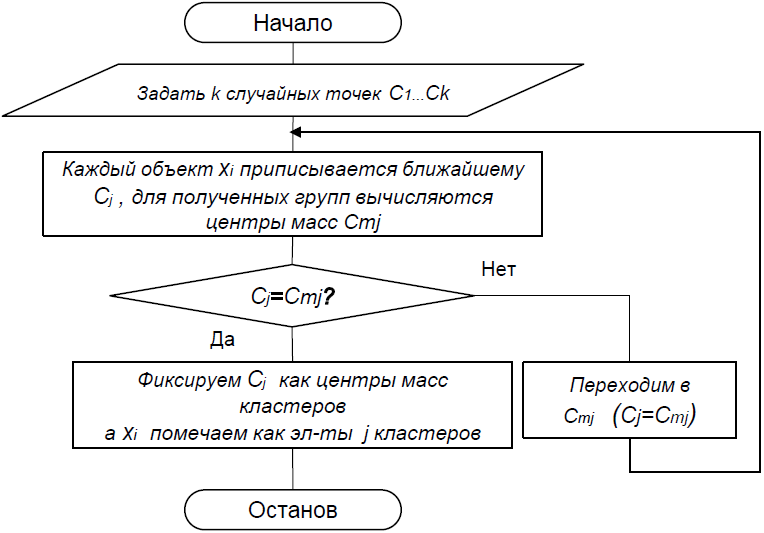
Блок-схема |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

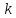 -средних
на примере
-средних
на примере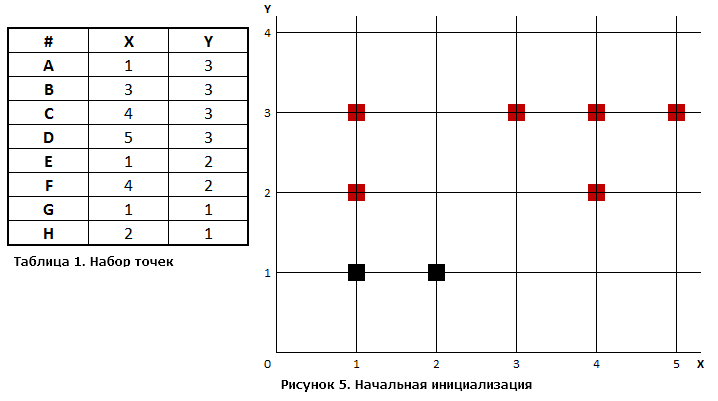
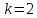 .
.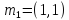 и
и
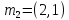 .
На рисунке они закрашены черным
цветом.
.
На рисунке они закрашены черным
цветом.
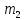
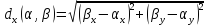
 ,
,
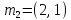 и каждой точкой исходного множества,
а также указано, к какому кластеру
принадлежит та или иная точка.
и каждой точкой исходного множества,
а также указано, к какому кластеру
принадлежит та или иная точка.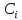 — точки
— точки
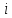 -того
кластера):
-того
кластера):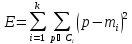

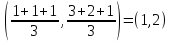 .
.
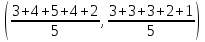
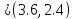 .
.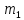
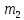
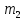 привело к тому, что запись H
оказалась ближе к центру
привело к тому, что запись H
оказалась ближе к центру
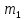 ,
что автоматически сделало ее членом
кластера 1. Все остальные записи
остались в тех же кластерах, что и на
предыдущем проходе алгоритма. Таким
образом, кластер 1 будет A, E,
G, H, а кластер 2 – B, C,
D, F. Новая сумма квадратов
ошибок составит (
,
что автоматически сделало ее членом
кластера 1. Все остальные записи
остались в тех же кластерах, что и на
предыдущем проходе алгоритма. Таким
образом, кластер 1 будет A, E,
G, H, а кластер 2 – B, C,
D, F. Новая сумма квадратов
ошибок составит (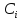 — точки
— точки
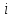 -того
кластера):
-того
кластера):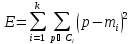
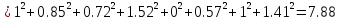

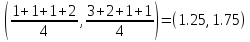 .
.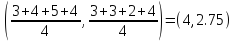 .
.