1.4. Вынужденные колебания в параллельном контуре

Параллельное соединение элементов контура L и C с источником внешней ЭДС образует параллельный колебательный контур.

Полное сопротивление (импеданс) простейшего параллельного контура (рис.7а) в комплексной форме, без учета внутреннего сопротивления R_i источника внешней ЭДС

(26)

где и — сопротивление его ветвей,

a знаменатель — полное сопротивление последовательного контура.

Модули сопротивления ветвей соответственно равны:

, .

Вблизи резонанса R << ωL, а из выражения (20), можно считать равным R. Тогда сопротивление Z₀ параллельного контура при резонансе, согласно (26), будет активным, максимальным и очень большим по величине

(27)

Если ω ≠ ω₀, сопротивление контура уменьшается и приобретает реактивный характер (при ω < ω ₀ — индуктивный, при ω > ω ₀ — емкостный).

Внутреннее сопротивление источника внешней ЭДС существенно влияет на работу параллельного контура. В этом случае ток в неразветвленной части цепи

а напряжение на контуре

При ток I_общ практически не зависит от и

Очевидно, что коэффициент передачи напряжения

a добротность Q, полоса пропускания 2∆ω и другие характеристики контура определяются практически только его параметрами L, C, R.

Если Z₀ сравнимо с R_i , то последнее шунтирует контур (эквивалентная схема рис.7б), резонансное сопротивление контура (эквивалентное) уменьшается.

(28)

добротность контура (эквивалентная) снижается

(29)

Здесь Q и R₀ соответственно собственные добротность и резонансное сопротивление контура (без учета влияния R_i ).

При этом К_U приближается к единице, но ухудшаются резонансные свойства и расширяется полоса пропускания 2∆ω параллельного контура

(30)

Резонансные кривые параллельных контуров (рис.8) по построению аналогичны резонансным кривым последовательных контуров, но могут быть противоположны по ходу кривой.

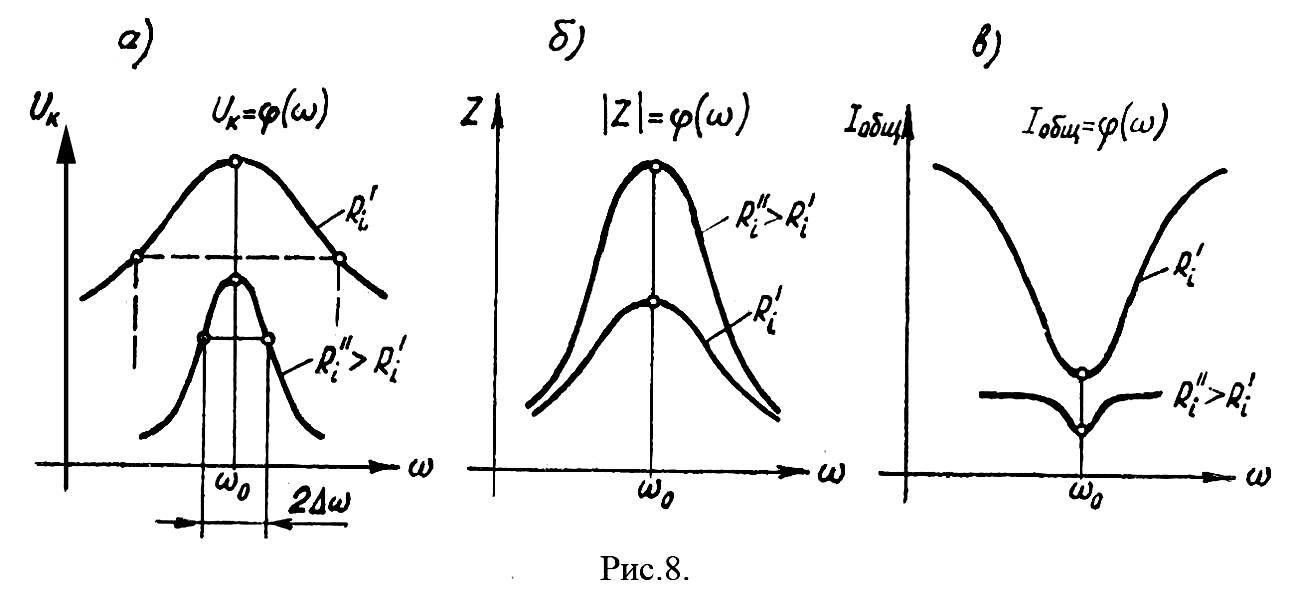
Параллельные контуры в радиотехнических устройствах применяются в качестве селективной нагрузки каскадов, обеспечивающей значительно большее усиление в полосе пропускания, чем за ее пределами, и для получения выигрыша в токе в ветвях контура от сигнала выделенной частоты.

2. Связанные колебательные контуры

2.1. Общие сведения

Одиночные колебательные контуры имеют непостоянный коэффициент передачи в области полосы пропускания и недостаточное подавление частот за ее пределами. Эти недостатки в значительно меньшей степени присущи связанным колебательным контурам.

Связанные контуры — система из двух или нескольких колебательных контуров, в которой изменения электрического состояния одного контура вызывает соответствующие изменения электрических состояний в других контурах. Связь между контурами осуществляется или через магнитное поле – индуктивная связь (трансформаторная – рис. 9,а; автотрансформаторная – рис.9,б) или через электрическое поле – емкостная связь (внутренняя – рис. 9,в; внешняя – рис. 9,г).

Система связанных контуров позволяет уменьшить влияние внутреннего сопротивления источника сигнала и нагрузки на контур и получать резонансные кривые близкие к П – образным или специальной формы.

В системе из двух связанных контуров одинаковые собственные частоты ₀ , во вторичном контуре наводится ЭДС

(31)

Здесь İ_1m — ток в первичном контуре, а Ż_CB — коэффициент пропорциональности, называемый сопротивлением связи. В зависимости от вида связи Ż_CB может иметь индуктивный, емкостной, активный или смешанный характер.

Связь между контурами характеризуется коэффициентом связи

Для индуктивной трансформаторной связи с взаимной индуктивностью М (рис. 9, а)

X_1СВ = ωL₁ , X_2СВ = ωL, X_СВ = ωM

Тогда

, а при (32)

Вторичный контур, в котором возникают вынужденные колебания, в свою очередь оказывает обратное воздействие на контур первичный, изменяя его параметры и внося в него добавочное сопротивление. Для двух связанных контуров второй закон Кирхгофа выражается системой уравнений:

в которой

;

(33)

Отсюда ток в 1-ом контуре

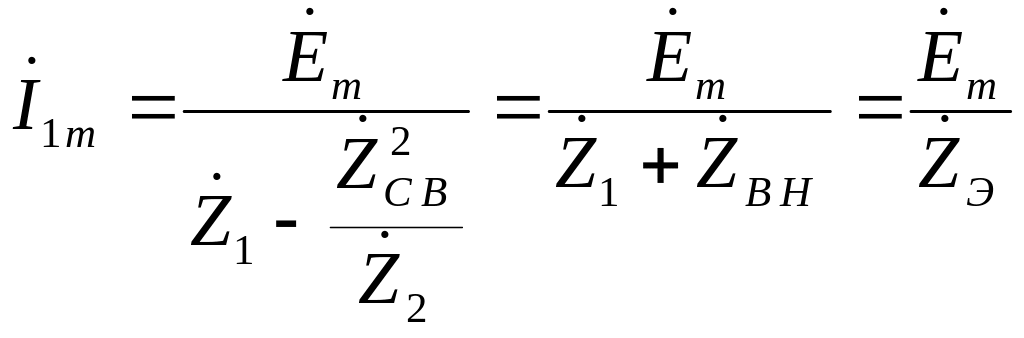(34)

где — называют вносимым сопротивлением.

а — эквивалентным сопротивлением.

Вносимое сопротивление можно выразить через параметры связанных контуров.

Обозначая

(35)

получаем

Тогда эквивалентное сопротивление равно:

(36)

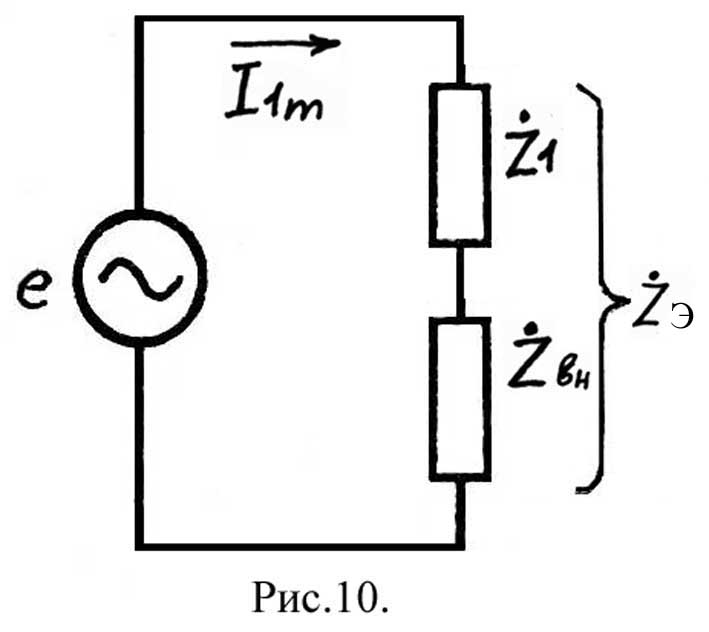
Введение понятий и позволяет заменить реальную систему связанных контуров (рис.9) ее эквивалентной схемой (рис.10).

Ток во 2-м контуре, учитывая (31) и (34),

(37)