5.11.Пример на вычисление условной вероятности зависимых событий

П р и м е р. В урне находятся 4 красных шара и 2 белых. Извлекается последовательно два шара.

1) Пусть первым шаром появился белый (Б1).

Найти вероятность того, что:

а) второй шар белый (Б2), б) второй шар красный (К2):

2) Пусть первым шаром появился красный (К1).

Найти вероятность того, что:

а) второй шар белый (Б2), б) второй шар красный (К2) при:

Решение.

Пусть

Б1 = {первый шар белый}; К1 = {первый шар красный};

Б2 = {второй шар белый}; К2 = {второй шар красный};

Тогда, условные вероятности легко подсчитать.

1. а) Р_Б1(Б2)=1/5; б) Р_Б1(К2)=4/5;

2. а) Р_К1(Б2)=2/5; б) Р_К1(К2)=3/5.

3) Найти вероятность того что появятся:

а) два белых; б) первый красный, второй белый;

в) первый белый второй красный; г) два красных шара;

Обрзначим 4 попарно несовместных событий:

К1К2 = два шара красных;

К1Б2 = первый шар красный, второй белый;

Б1К2 = первый шар белый, второй красный;

Б1Б2 = два белых шара.

Эти четыре случая образуют полную группу попарно несовместных событий (сумма их вероятностей должна быть равна единице) и в результате опыта появится только одно из них)

а) ;

Проверка с помощью комбинаторных формул: 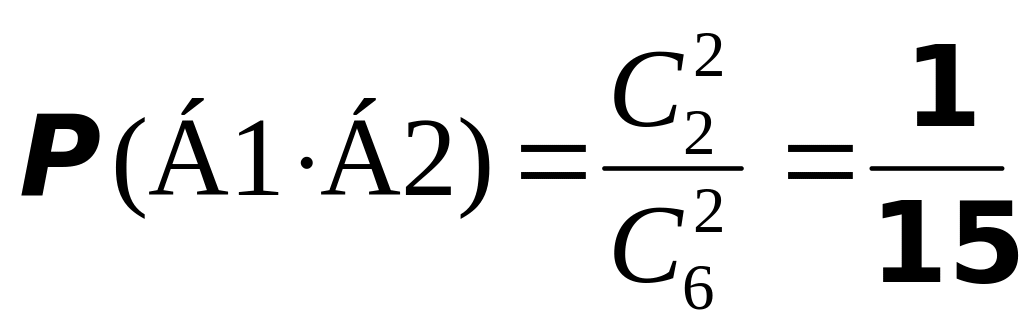. Задача решена правильно.

б)

Проверка: .

в) .

Проверка: .

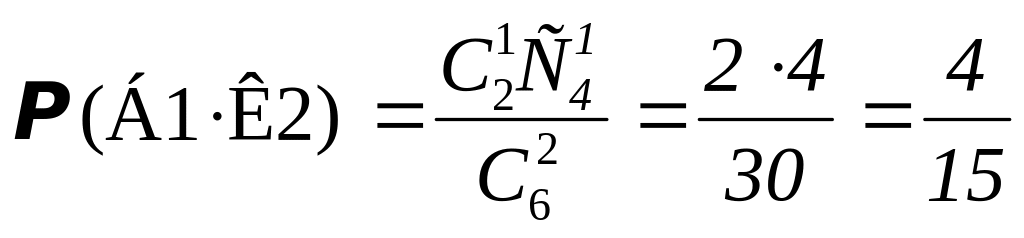г)

Проверка: .

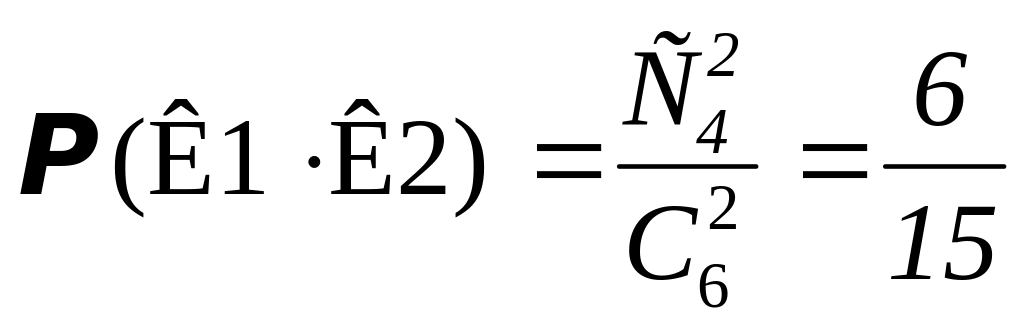4) Найти вероятность того, что среди двух вынутых появится ровно один белый шар.

Решение.

Событие А= {среди двух вынутых появится ровно один белый шар} = К1Б2 + Б1К2.

Вероятность P (А) можно вычислить используя формулу сложения вероятностей, учитывая то, что К1Б2 и Б1К2 есть несовместные события можно воспользоваться формулой для двух несовместных событий

P(С + D) = P(C) + P(D)

поэтому

P(А) = P(К1Б2 + Б1К2) = P(К1Б2)+Р(Б1К2) = 4/15 + 4/15= 8/15

5) Найти вероятность того, что среди двух вынутых появится хотя бы один белый шар.

Решение.

Событие В = { среди двух вынутых появится хотя бы один белый шар} = К1Б2 + Б1К2 + Б1Б2 .

Вероятность P (В) можно вычислить используя формулу сложения вероятностей, учитывая то, что К1Б2 и Б1К2 и Б1Б2 есть несовместные события можно воспользоваться формулой для трех несовместных событий

P(С + D+ Е) = P(C) + P(D) + Р(Е)

поэтому

P(В) = P(К1Б2 + Б1К2 + Б1Б2) = P(К1Б2)+Р(Б1К2) = 4/15 + 4/15 + 1/15= 9/15

Замечание. Событие В и событие К1К2 противоположны, поэтому вероятность P(В) можно было вычислить по формуле для противоположных событий

P(В) = 1 Р(К1К2) = 1 6/9 = 9/15.

П р и м е р. В барабане револьвера находятся 4 патрона из 6 возможных в произвольном порядке. Барабан раскручивают, после чего нажимают на спусковой крючок один раз и тут же второй раз. Найти вероятности того что при двух нажатиях произойдут:

1) два выстрела 2) один выстрел в) две осечки г) хотя бы один выстрел.

Пусть

А = {выстрел при первом нажатии};

{осечка при первом нажатии};

{выстрел при втором нажатии};

={осечка при втором нажатии}.

Имеется 4 попарно несовместных событий, которые можно найти с помощью умножения событий

 два выстрела подряд;

 первый выстрел, вторая осечка;

 первая осечка, второй выстрел;

 две осечки.

Эти четыре случая образуют полную группу попарно несовместных событий (сумма их вероятностей должна быть равна единице) и в результате опыта появится только одно из них)

События которые можно найти с помощью сложения событий

 один выстрел;

− хотя бы один выстрел.

Найдем вероятности этих событий используя формулу умножения вероятностей для зависимых событий

1)

Вероятность выстрела при первом нажатии на курок (событие А) равна . Если в первом случае произошел выстрел, то в барабане осталось только 3 патрона, причем они распределены по 5 гнездам, т.к. при втором нажатии на курок напротив ствола не может оказаться гнездо, в котором был патрон при первом нажатии на курок. Поэтому . Итак вероятность двух выстрелов подряд равна .

2. Вероятность того, что при первом нажатии появится выстрел, а при втором осечка вычислим рассуждая аналогично.

− первый выстрел, вторая осечка.

Аналогично

 первая осечка, второй выстрел.

Вероятность одного выстрела при двух нажатиях равна сумме вероятностей несовместных событий .

= .

3) Вероятность хотя бы одного выстрела равна

.

4) Рассуждая аналогично вычислим вероятность двух осечек подряд

− две осечки подряд.

Замечание. Две рассмотренные задачи по математическому существу дела ничем не отличаются.

Пример 3. В барабане револьвера находятся 4 патрона из 6 возможных в произвольном порядке. Барабан раскручивают, после чего нажимают на спусковой крючок один раз. Затем барабан вновь раскручивается и нажимают на спусковой крючок еще один раз. Найти вероятности того что при двух нажатиях произойдут:

1) два выстрела 2) один выстрел в) две осечки г) хотя бы один выстрел.

Замечание. Отличие третьей задачи от предыдущих двух является то, что условные вероятности вычисляются таким образом, что в знаменателе вместо 5 должно стоять 6. Последовательность вычислений одна и та же.