2. Теорема умножения вероятностей

Для вычисления вероятностей составных событий кроме теоремы сложения применяется теорема умножения. Здесь возникают новые понятия: произведение событий и условная вероятность.

5.6.Произведение двух событий

П р и м е р 1. Пусть эксперимент состоит в подбрасывании 2 монет одновременно. В результате эксперимента первая может упасть орлом вверх (О), а может упасть решкой вверх (Р). То же самое относится и ко второй монете, которая тоже может выпасть “орлом” вверх, либо решкой “вверх”. В результате проведения такого эксперимента имеется четыре непосредственных события ОО, ОР, РО, РР.

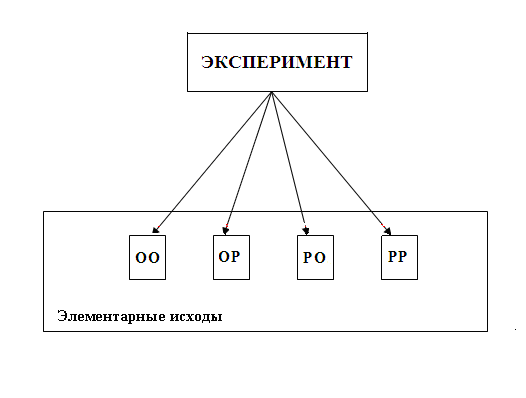
Рис.2. Эксперимент по подбрасыванию двух монет и элементарные исходы.

Пусть

А = { только на одной из монет появляется орел О или на обоих решка Р } = ОР+РО +PP.

В = { на первой О , а на второй О или Р } = ОО+ОР.

Видно, что события А и В совместны т.к. элементарный исход ОР входит в событие А и в событие В. Если в результате эксперимента появляется исход ОР, то это может рассматриваться как событие С состоящее в одновременном появлении события А и события В при подбрасывании двух монет. Это записывают так

С = А  В (или С =А ⋂ В).

Произведением двух событий А и В называется событие С, которое состоит в совместном появлении этих событий в эксперименте и обозначается как С = А  В.

П р и м е р 1. Пусть сложный эксперимент состоит в подбрасывании 3 монет. Элементарным исходом сложного эксперимента будет какая то одна комбинация из букв О или Р в трёх позициях. OOO, OOP, OPO, OPP, POO, POP, PPO, PPP.

Пусть А = { на одной монете появляется О } = ОРР+РОР+РРО .

Пусть В = ООР+ОРО+ОРР+РОО.

Видно, что события А и В совместны. Если исход эксперимента ОРР, то это может рассматриваться как событие С состоящее в одновременном появлении события А и события В. Это записывают так С = А  В (или С =А ⋂ В).

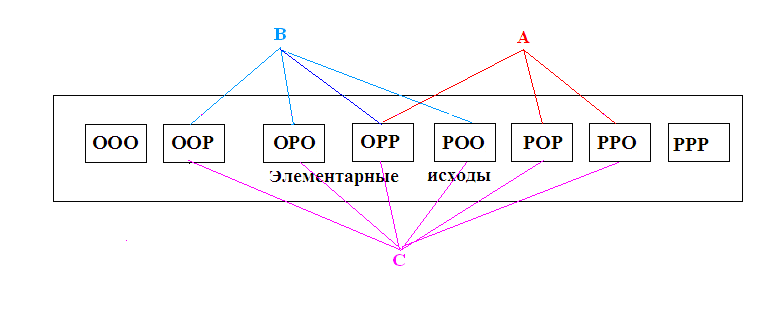
Рис. Элементарные и сложные события.

Если два события несовместны, то их произведение есть невозможное событие С = А  В = .

Например, Пусть А = ОРР + РОР + РРО, В = ООР + ОРО, тогда А и В несовместны, у них нет общих событий.

Определение. Пересечением или произведением событий A_k называется событие А, которое заключается в осуществлении всех событий A_k.

Рассмотри пример который близок к эксперименту по подбрасыванию двух монет.

Пример 2.

Два орудия стреляют по цели. Событие А ={ поражение цели первым орудием }, тогда пусть есть противоположное событие , т.е. первое орудие промахнулось. В = { поражение цели вторым орудием } и тогда есть противоположное событие, т.е. второе орудие промахнулось. Имеем совокупность четырех элементарных исходов АВ, В, А , . Каждое из этих событий есть произведение двух событий. АB = A  B или АB = A⋂B и т.д..

5.7.Пример на вычисление вероятности произведения событий

С понятием произведения двух событий тесно связано понятие зависимых и независимых событий и соответственно условной и безусловной вероятности. Это наиболее трудный для восприятия материал, поэтому рассмотрим пример в котором используются эти понятия, и постараемся понять их интуитивно, а в дальнейших параграфах введем их строгие определения.

Пример.

Пусть подбрасывается две монеты. Этот эксперимент можно рассматривать как сложный, состоящий из двух экспериментов. Первый эксперимент состоит в подбрасывании первой монеты, а второй эксперимент состоит в подбрасывании второй монеты.

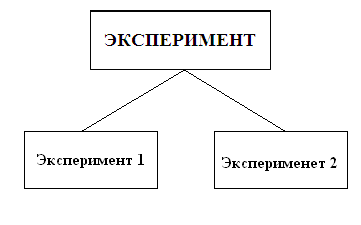
В каждом простом эксперименте может появиться Орел или Решка О1, Р1, О2, Р2.

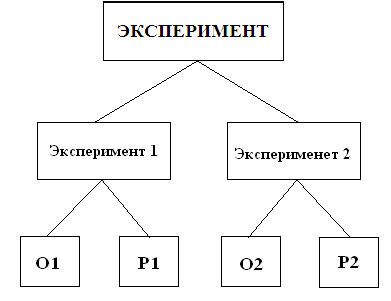
Из этих простых исходов образуются 6 сложных событий, равное количеству сочетаний из 4 по 2

Это будут произведения событий:

О1Р1, О1О2, О1Р2, Р1О2, Р1Р2, О2 Р2.

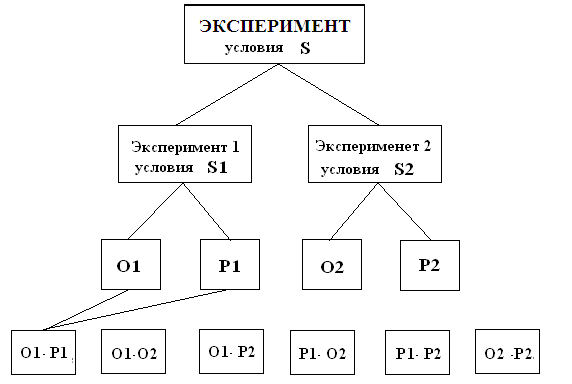
Вычислим вероятности появления сложных событий. Вероятности событий О1, Р1 при условии, что S1 произошло равны по 1/2. Вероятности событий О2, Р2 при условии что S2 произошло то же равны по 1/2. Поэтому можно записать условные вероятности

P_S1(O1)= P_S1(Р1)= P_S2 (O2) =P_S2 (Р2)=1/2 .

Тогда вероятности совместных событий должны подсчитываться по формулам для произведения событий

Р(О1Р1), Р(О1О2), Р(О1Р2), Р(Р1О2), Р(Р1Р2), Р(О2 Р2)

Два из этих шести событий невозможны: О1Р1= и О2Р2=, Поэтому их вероятности равны нулю

Р(О1Р1)=0, Р(О2 Р2) =0.

Отметим, что из 6 простых событий можно получить и другие невозможные события, например О1О1, О1О1+ О2, Р1Р2, О1О1 Р1, и т.д. до бесконечности. Однако эти события бессодержательны, они невозможны.

Остальные четыре вероятности можно подсчитать по формуле для независимых событий.

Р(О1О2)=(1/2)(1/2)=1/4,

Р(О1Р2)= (1/2)(1/2)=1/4,

Р(Р1О2)= (1/2)(1/2)=1/4,

Р(Р1Р2)= (1/2)(1/2)=1/4.

Знак умножения и цифры обозначающие эксперименты можно не ставить и получим

P(ОО)=1/4, P(ОР)=1/4, P(РО)=1/4, P(РР)=1/4.

Мы получили вероятности которые раньше подсчитывали по классической формуле для равновозможных, несовместных и образующих полную группу событий и ОО, ОР, РО, РР.

Замечание 1. В данной постановке задачи по подбрасыванию двух монет рационально рассматривать события ОО, ОР, РО, РР как элементарные (непосредственные) исходы эксперимента. Вообще говоря, любой исход в этом примере, например ОР можно представить в виде совместного появления двух ещё более элементарных исходов: “орёл” на первой монете и “решка 2” на второй и тогда ОР есть совместное появление двух исходов орла на 1 и решка на 2. Но этот вопрос мы отложим до параграфа.

Из этого замечания следует, что событие может считаться элементарным даже тогда, когда оно разложимо на ещё более простые события.