Непрерывные случайные величины
5.31.Функция распределения непрерывной с.В.
Как мы уже были приведены примеры, кроме д.с.в. имеются и непрерывные случайные величины (н.с.в.). Еще пример н.с.в.
Пример 1 Пусть на интервале (a, b) ставится произвольно точка х. Тогда длина Х= хa есть случайная непрерывная величина. Можно рассматривать идеализированный опыт и считать, что точка бросается на отрезок совершенно произвольно. Вероятность того что длина отрезка Х = x-a окажется в точности равной заданному отрезку l < b-a , равна нулю так как значениями X являются действительными числами.
Пример 2. В телефонном справочнике телефонные номера имеют 6 и более цифр. Пусть совершенно произвольно выбираются страницы справочника, берётся наугад номер, берутся в нём 4 последние цифры, образующие четырехзначное число и оно делится на 10000. Тогда в результате каждого выбора мы будем иметь случайное число значения которой заключены в интервале (0, 1). Можно сказать что имеем непрерывную случайную величину Х с равномерным распределением все значения которой заключены в интервале (0, 1).
Во
всех примерах с непрерывными случайными
величинами нельзя поступить по аналогии
с д.с.в. Нельзя построить закон
распределения
,
так как нет дискретных значений, которые
принимает с.в. с какими то определёнными
вероятностями. Однако определение
функции распределения
годится как для д.с.в , так и для н.с.в.
Вполне можно поставить вопрос в примере
1 или 2, чему равна вероятность того, что
н.с.в. в результате эксперимента примет
значение меньшее x
и задать функцию
.
В
примере 1 функцию
разумно задать линейную.
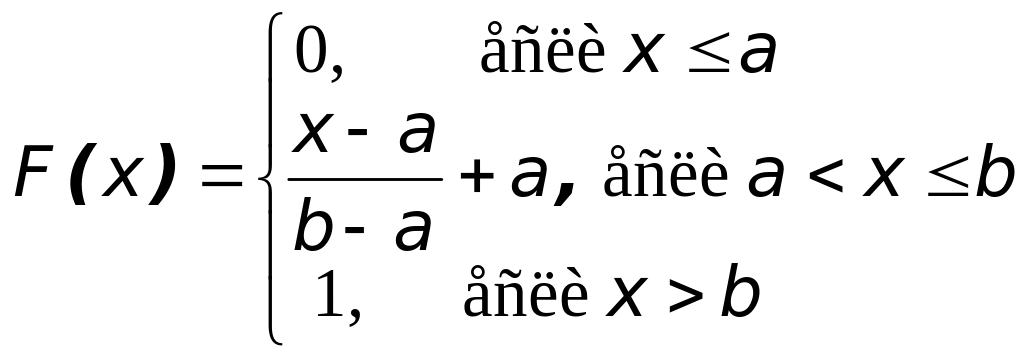
Смысл такой функции распределения заключается в том, что при росте x “накопленная вероятность” равномерно растёт по линейному закону. Другой смысл рассмотрим позже, с точки зрения закона распределения.
Например, пусть концы интервала (a, b) равны а=0, b=2. Тогда функция имеет вид
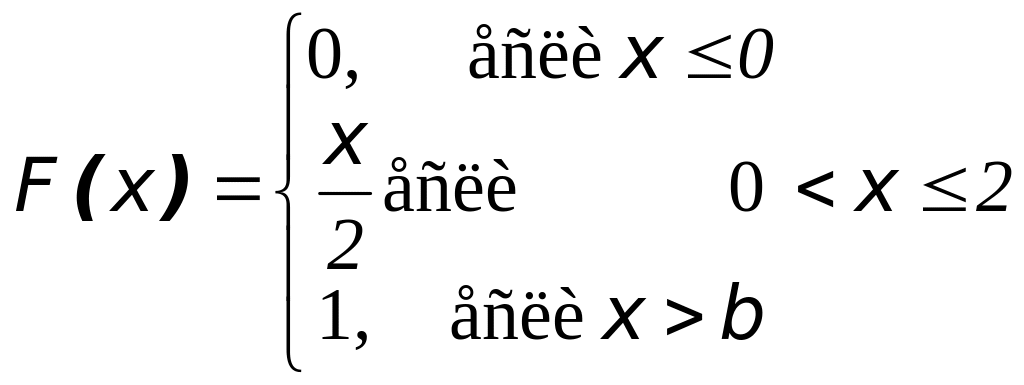
И имеет график
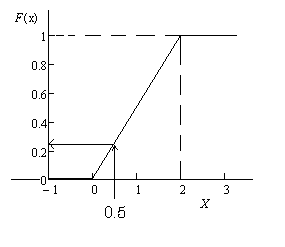
Для
того чтобы узнать, какова вероятность
того, что с.в. примет значение меньшее,
скажем, 1/2 нужно подставить это значение
в функцию распределения
,
Определение функции распределения н.с.в. не отличается от соответствующего определения для д.с.в.
Определение. Функцией распределения случайной величины (безразлично дискретной или непрерывной) называют функцию F(x), с помощью которой определяют вероятность, того, что в результате эксперимента случайная величина примет значение меньшее x, т.е.
.
5.32.Закон распределения н.С.В.
Для закона распределения н.с.в. как раз наоборот. Определение для н.с.в должно отличаться от определения закона распределения для д.с.в., так как уже было сказано, что значения непрерывной с.в. есть действительные числа из сплошного промежутка (интервала) (a, b). Чтобы лучше понять способ введения определения закона распределения для н.с.в. рассмотрим физическую задачу.
Пример. Дан кусок металла массой 1 кг. Из него сделаны вытянута проволока с постоянной (равномерной) плотностью металла. Проволока имеет длину 2 м. Раз плотность по длине постоянна, то она равна f(x)=(x)=1/2 кг/м. На графике это есть постоянная функция.
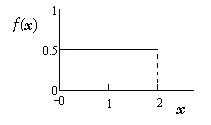
Чтобы найти массу проволоки длиной x < 2 нужно плотность умножить на длину m(x) = x, так как константа.
Если
(x)
изменяется по длине, то вычислить массу
можно вычислить с помощью интеграла
.
Тогда график m(x) при = 1/2 кг/м будет линейной функцией.
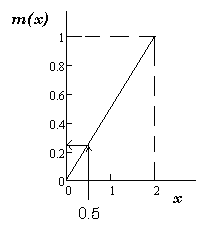
Чтобы найти массу проволоки длиной x можно по графику. Например, при х=0.5 м масса m равна 0.25 кг. Наоборот, если задана функция массы проволоки от длины х можно найти с помощью дифференцирования
.
Вполне
аналогично введем определение плотности
распределения
непрерывной случайной величины.
Определение. Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(x) первую производную от функции распределения F(x):
.
Тогда функция распределения непрерывной с.в. выражается через закон распределения f(x) с помощью интеграла
.