
- •Часть 1
- •Теорема сложения вероятностей для несовместных событий.
- •5.1.Сумма двух несовместных составных событий.
- •5.2.Сумма двух совместных событий
- •5.3.Вероятность суммы двух несовместных событий.
- •5.4.Полная группа событий
- •5.5.Противоположные события.
- •Теорема умножения вероятностей
- •5.6.Произведение двух событий
- •5.7.Пример на вычисление вероятности произведения событий
- •5.8.Условная вероятность
- •5.9.Теорема умножения вероятностей для зависимых событий
- •5.10.Вероятность произведения двух независимых событий
- •5.11.Пример на вычисление условной вероятности зависимых событий
- •5.12.События независимые в совокупности.
- •5.13.Теорема умножения для n независимых событий
- •5.14.Совместное применение теорем сложения и умножения вероятностей
- •5.15.Вероятность появления хотя бы одного из событий независимых в совокупности.
- •Следствия теорем сложения и умножения
- •5.16.Вероятность суммы двух совместных событий
- •1) Если события а и в несовместны, то
- •2) Если события а и в совместны и зависимы то
- •3) Если события а и в совместны и независимы то
- •5.17.Формула полной вероятности
- •5.18.Формула Бейеса (формула гипотез)
- •Повторение испытаний.
- •5.19. Формула Бернулли
- •5.20.Наивероятнейшее число появления события в независимых испытаниях
- •Дискретные случайные величины и законы их распределения
- •5.21.Случайная величина
- •5.22.Закон распределения вероятностей дискретной случайной величины
- •5.23.Закон и функция равномерного распределения д.С.В.
- •5.24.Закон и функция биномиального распределения
- •5.25.Асимптотические формулы биномиального распределения
- •1. Формула Лапласа.
- •5.26.Простейший поток событии
- •5.27.Гипергеометрическое распределение
- •5.28. Выводы
- •Числовые характеристики дискретных случайных величин
- •5.29.Математическое ожидание
- •5.30.Дисперсия и среднеквадратичное отклонение
- •Непрерывные случайные величины
- •5.31.Функция распределения непрерывной с.В.
- •5.32.Закон распределения н.С.В.
- •5.33.Вероятность попадания непрерывной с.В. В заданный интервал
- •5.34.Вероятностный смысл плотности распределения вероятности н.С.В.
- •Числовые характеристики непрерывных случайных величин
- •Законы распределения для случайных непрерывных велич
- •5.35.Равномерное распределение
- •5.36.Нормальное распределение
5.30.Дисперсия и среднеквадратичное отклонение
Определение. Дисперсией (рассеиванием) дискретной случайной величины X называется математическое ожидание квадрата отклонения случайной величины X от ее математического ожидания M(X)
![]() ,
,
где
![]() случайная
величина равная отклонению случайной
величины X от своего математического
ожидания. Случайная величина
является центрированной, её математическое
ожидание равно нулю M()
= 0. Однако математическое ожидание от
квадрата центрированной величины будет
всегда положительным числом. Геометрически
корень квадратный из дисперсии
характеризует “рассеивание” случайной
величины X вокруг своего
математического ожидания.
случайная
величина равная отклонению случайной
величины X от своего математического
ожидания. Случайная величина
является центрированной, её математическое
ожидание равно нулю M()
= 0. Однако математическое ожидание от
квадрата центрированной величины будет
всегда положительным числом. Геометрически
корень квадратный из дисперсии
характеризует “рассеивание” случайной
величины X вокруг своего
математического ожидания.
Определение. Средним квадратическим отклонением случайной величины Х называется число равное квадратному корню из дисперсии
![]() .
.
Пример. Пусть бросается монета. Выпадению О(рла ) припишем случайной величине Х значение 1, а при выпадении Р(ешки) припишем Х значение 2. Найти математическое ожидание, дисперсию и среднеквадратическое уклонение.
Решение.
Математическое ожидание равно М(X) = 1 1/2 + 2 1/2 = 1,5. Заполняем таблицу
-
Xi
1
2
Pi
1/2
1/2

1/2
1/2

1/4
1/4
Вычисляем дисперсию
D(X)= M(2) = 1/4 1/2 + 1/4 1/2 = 1/4.
Среднее квадратичное отклонение случайной величины X равно
![]() .
.
Мы получили, в общем, тривиальный результат. Уклонение Х от математического ожидания равно = 1/2, т.е. значения случайной величины X = 1 или Х = 2 отстоят от математического ожидания на длину = 1/2.
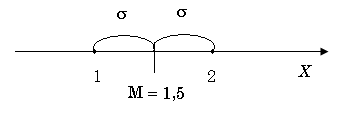
П р и м е р 1. Пусть эксперимент состоит из двух испытаний. Каждое испытание состоит в подбрасывании 1 одной и той же монеты. В каждом испытании по подбрасыванию одной монеты О(рел) появляется с вероятностью Р(О) = p = 1/2. В этих двух испытаниях О может:
а) не появиться вовсе, б) может появиться только один раза, в) может появиться два раза.
В этом эксперименте случайная величина X принимает значения Х= {0, 1, 2}. Вероятности появления этих чисел Р2 (k) , где k = 0, 1, 2, мы уже рассчитали ранее по упрощенной формуле Бернулли.
Р2 (0) = ; Р2 (1) = ;
Р2 (2) = . Имеем таблицу для биномиального закона
Хi |
0 |
1 |
2 |
pi |
1/4 |
1/2 |
1/4 |
|
-1 |
0 |
1 |
|
1 |
0 |
1 |
Найти математическое ожидание, дисперсию и средне- квадратичное уклонение.
Р е ш е н и е.
М(X) = 0 1/4 + 1 1/2 + 2 1/4 = 1
D(X)= M(2) = 1 1/4 + 0 1/2 + 1 1/4 = 1/2.
![]()
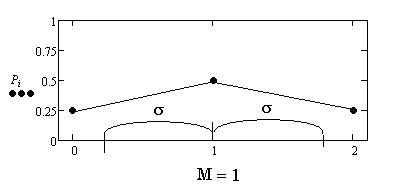
Свойство характеризовать рассеивание случайной величины хорошо будет видно на следующем примере.
Пример.
Эксперимент состоит в том, что два стрелка разной квалификации стреляют по 20 раз в мишень. Результаты (очки) от 4 до 10 попадания в мишень приведены в таблице.
Очки |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
1 стрелок |
3 |
7 |
6 |
4 |
|
|
|
2 стрелок |
1 |
2 |
4 |
5 |
3 |
3 |
2 |
Построить законы распределения, найти математические ожидания, среднеквадратичные уклонения.
Решения. Для каждого из стрелков постоим таблицы. В качестве вероятностей возьмем частоту.
1 стрелок
Очки Xi |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
1 стрелок |
3 |
7 |
6 |
4 |
|
|
|
p |
3/20 |
7/20 |
6/20 |
4/20 |
|
|
|
|
1,55 |
0,55 |
-0,45 |
-1,45 |
|
|
|
|
2.40 |
0.30 |
0.20 |
2.10 |
|
|
|
М(X) = 10 3/20 + 9 7/20 + 8 6/20 + 7 4/20 = 8,45
D(X)= M(2) = 2.4 3/20+0.37/20+0.26/20+2.14/20 =0,945
![]()
2 стрелок
Очки Xi |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
2 стрелок |
1 |
2 |
4 |
5 |
3 |
3 |
2 |
p |
1/20 |
2/20 |
4/20 |
5/20 |
3/20 |
3/20 |
2/20 |
|
3,2 |
2,2 |
1,2 |
0,2 |
0,8 |
1,8 |
2,8 |
|
10,24 |
4,84 |
1,44 |
0,04 |
0,64 |
3,24 |
7,87 |
М(X) = 10 1/20 + 9 2/20 + 8 4/20 + 7 5/20 +6 3/20 + 5 3/20 + 4 2/20 = 6,8
D(X)= M(2) = 10,24 1/20 + 4,84 2/20 + 1,44 4/20 + 0,04 5/20 +0,64 3/20 + 3,24 3/20 + 7,87 2/20 = 2,66
![]()
Из сравнения результатов вычислений M и можно сделать вывод, что первый стрелок имеет математическое ожидание ближе к 10, чем у второго стрелка. Среднеквадратичное уклонение меньше у второго стрелка, это означает, что пули первого стрелка лежаться ближе к математическому ожиданию, чем у второго стрелка или как говорят “кучность” стрельбы у первого стрелка лучше. В идеале требуется, чтобы М ожидание было бы равно 10 и среднеквадратичное уклонение равно нулю. Так мог бы стрелять автоматическое устройство, жестко закрепленное и отлаженное на попадание в центр.
На практике подобный способ вычисления дисперсии неудобен, т.к. приводит при большом количестве значений случайной величины к громоздким вычислениям.
Второй способ вычисление дисперсии.
Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания.
![]()
Применим эту формулу для рассмотренного выше примера для первого стрелка:
Очки Xi |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
(Xi)2 |
100 |
81 |
64 |
49 |
36 |
25 |
16 |
1 стрелок ni |
3 |
7 |
6 |
4 |
|
|
|
pi |
3/20 |
7/20 |
6/20 |
4/20 |
|
|
|
М(X2) = 100 3/20 + 81 7/20 + 64 6/20 + 49 4/20 = 72,35
Тогда дисперсия равна
D(X)= 72,35 (8.45)2 = 0.948
Что совпадает, в пределах точности вычислений, с результатом, подсчитанным первым способом.
