5.22.Закон распределения вероятностей дискретной случайной величины

Для задания дискретной случайной величины необходимо указать все её возможные значения и указать вероятности появления этих значений в эксперименте.

Законом распределения дискретной случайной величины называют функцию (соответствие) между возможными её значениями и их вероятностями .

Как известно, функцию можно задать тремя способами:

1) аналитическим (с помощью формулы),

2) таблично (с помощью таблицы)

3) в системе координат (с помощью графика).

Для дискретных случайных величин, основным способом задания закона является табличный, который более нагляден, но с ним, конечно, неразрывно связаны и два других способа.

5.23.Закон и функция равномерного распределения д.С.В.

Пример 1. Пусть подбрасывается монета. Если выпадет О(рел), то припишем этому событию значение 1, если выпадет Р(ешка), то припишем этому событию значение 2. Можно сказать, что в результате эксперимента появляется случайная величина X имеющая всего два значения 1 или 2. Вероятности этих значений равны по 1/2.

Замечание. Значение случайной величине можно было приписать и 0 и 1, как в предыдущем параграфе или другие значения. Это зависит от назначения задачи, но выбор значений не влияет на все дальнейшие рассуждения по существу математического дела. Саму с.в. обозначили буквой Х, вместо .

1)Закон можно задать следующей простой таблицей.

X	x1= 1	x2 =2
p	1/2	1/2

2)Аналитическая формула закона совсем простая

3)Графически закон будет изображаться дискретным графиком

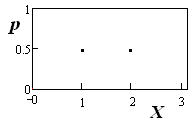
Областью определения закона распределения является два значения X = x: 1 , 2. Областью значений закона является одно значение P=p: 0.5.

В результате эксперимента случайная величина X принимает одно и только одно из значений x₁ = 1 или x₂ = 2 . Эти события образуют полную группу несовместных событий и поэтому сумма вероятностей равна р₁+р₂=1.

Определение.Равномерным распределением д.с.в. является такой закон распределения, когда все значения с.в. x_{i ,} i=1, n появляются с одной и той же вероятностью p= 1/n.

Имея закон распределения легко построить и функцию распределения.

Познакомимся с функцией распределения.

Пусть x ∊ R действительное число, R  множество действительных чисел. В законе распределения указана вероятность события x = x_i. Зададимся вопросом, о том, чему равна вероятность P события x < x_i . Это и будет функцией распределения, которую обозначают F(x).

Определение. Функцией распределения случайной величины (безразлично дискретной или непрерывной) называют функцию F(x), с помощью которой определяют вероятность, того, что в результате эксперимента случайная величина примет значение меньшее x , т.е.

Имея закон распределения легко построить и функцию распределения .

Построим её для нашей задачи.

а)Пусть x ≤ x₁ =1. Тогда вероятность того, что случайная величина примет значение меньшее 1, очевидно равно нулю P(X < 1) = 0, так как при выпадении орла, с.в. принимает значение 1, а решки значение 2 и меньшее значение выпасть не может.

б) Пусть число x заключено в полуинтервале x₁= 1 < x ≤ x₂ =2 тогда вероятность P(X < x) =1/2. Вероятность события 1< X≤ 2 равна 1/2, так как при выпадении орла, с.в. принимает значение 1, а решки значение 2 и если взять, например x = 1.3 , то вероятность того, что с.в. примет значение X меньшее x=1.3 будет только в том случае, когда выпадет орёл, а это событие осуществляется с вероятностью 1/2.

c) Пусть x > x₂ =2 , Вероятность события X < х равна 1, так как при выпадении орла, с.в. принимает значение 1, а решки значение 2 и если взять, например x = 2.2 , то вероятность того, что с.в. примет значение X меньшее x=2.2 будет осуществляется всегда. При любой реализации эксперимента по подбрасыванию монеты, получим X равное либо 1, либо 2 и в любом случае это меньше чем 2.2.

Запишем результат этих рассуждений в виде аналитической формулы

.

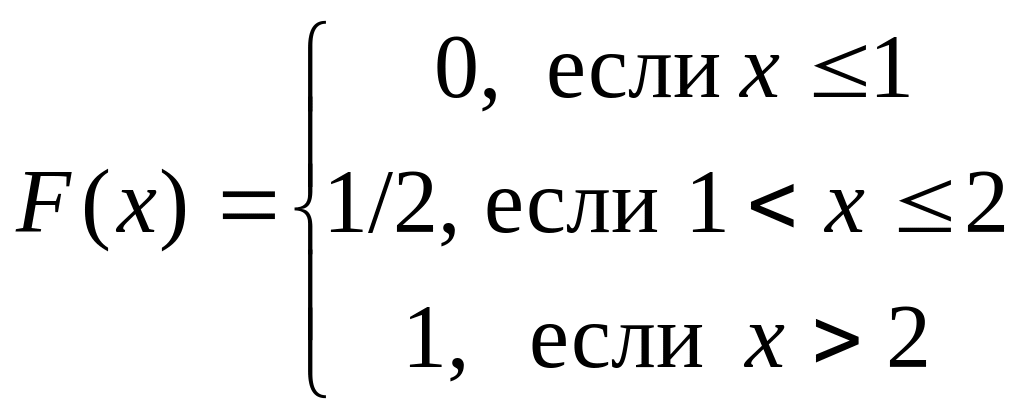Функцию можно рассматривать как сумму вероятностей , где , за исключением самих точек , когда . Таким образом , назначение функции распределения отражать “накопление” вероятности.

График этой функции представляется в виде кусочнопостоянной функции, имеющее разрывы первого рода в двух точках.

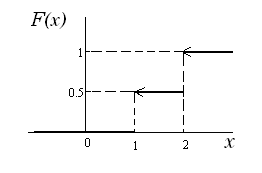
Следует отметить, что оба способа задания с.в. ( с помощь закона и функции распределения) совершенно равноправны и, имея одну из них, всегда можно построить другую.

Областью определения функции F(x) является все множество действительных чисел X = x:  < x < + . Областью значений функции является отрезок P = p: 0 ≤ p ≤ 1.

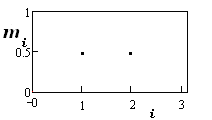
Пример. Дан кусок металла массой 1 кг. Из него сделаны 2 шар массами m₁ = 1/2 (кг/шар) и m₂ = 1/2 (кг/шар). Для большей аналогии с предыдущей вероятностной задачей, шары будем нумеровать с нуля:

10.5; 20.5.

Функция , отражающую зависимость массы шара от номера шара будет иметь в точности вид на рис.

Требуется построить функцию , k = 1  2 , которая равна массе всех шаров от 0 до k, где k  меняется от 0 до 2. По этой функции построить функцию , где [х]  целая часть от действительного числа x.

Решение дано на следующих рисунках.

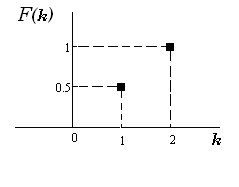
На этом графике ордината первой точки соответствует массе первого шара, ордината второй точки сумме масс первого и второго шара.

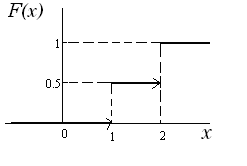
Этот график получен из предыдущего, по формуле , где [х]  целая часть от действительного числа x. Он отражает как бы “накопляемую массу” при переходе от номера шара к следующему номеру. С физической точки зрения он конечно не даёт ничего нового по сравнению с графиком , k = 1  2, но практически идейно совпадает с функцией распределения вероятностей.

П р и м е р 2. Пусть эксперимент состоит в подбрасывании 2 монет одновременно. В результате проведения такого эксперимента имеется четыре результата ОО, ОР, РО, РР, которым припишем номера 0, 1, 2, 3. Говорят, что при проведении эксперимента случайная величина X может принят четыре числовых значений X = x: 0, 1, 2, 3.

1) Табличный способ. Закон можно задать следующей простой таблицей.

Х	x1= 0	x2 =1	x3= 2	x4= 3
pi	1/4	1/4	1/4	1/4

В результате эксперимента случайная величина принимает одно и только одно из значений X=x₁ = 1 или Х=x₂ = 2 или X=x₃ = 3 или Х=x₄ =4 . Эти события образуют полную группу несовместных событий и поэтому сумма вероятностей равна р₁ + р₂ + р₃ + р₄ = 1.

2) Графический способ. Мы имеем функцию р = р(x_i) которую можно изобразить графически.

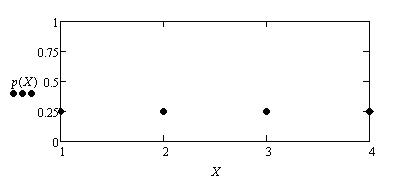
Из таблицы и графика хорошо видно, что значения дискретной случайной величины 1, 2, 3, 4 появляются в эксперименте с одной и той же вероятностью равной 1/4.

3) Функцию можно задать и аналитически с помощью формулы.

Область определения функции есть множество X ={ 1, 2, 3, 4}, а областью значений P = 1/4, сама функция задается простой формулой

P(x_i) = 1/4 , i=1, 4.

В этой функции аргументом является переменная дискретная величина Х. Функцией является величина вероятности появления того или иного значения x_{i .}

Рассмотренные два примера дают представление о простейшем равномерном законе распределения.

Функцию распределения легко построить. Она будет кусочно постоянной, с тремя точками разрыва. Область определения и область значений не отличаются от предыдущего примера с одной монетой.