Министерство образования и науки Российской Федерации
КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
К.А. ЛЕБЕДЕВ
С.С. СУЛЕЙМАНОВ
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Учебное пособие
Часть 1
Допущено отделением Научно-методического совета
по математике Министерства образования и науки РФ
и ЮФО в качестве учебного пособия для студентов
и школьников
Краснодар
2012
Теорема сложения вероятностей для несовместных событий.
5.1.Сумма двух несовместных составных событий.
Мы уже показали, что нужно понимать под составным событием. Показали, что есть аналогия между образованием натурального числа и образованием составного события.
Теперь покажем, что нужно понимать под суммой двух составных событий. Вновь обратимся к аналогии со сложением двух натуральных чисел. Когда складываются два натуральных числа, например 2+3, то в результате появляется третье число, которое есть объединение единиц двух исходных чисел, т.е. 2 + 3 = 1+1 + 1+1+1 = 5. Сумма 5, имеет столько же единиц, сколько имеют оба слагаемых 2 и 3 вместе. Сумма есть объединение единиц, из которых состоят слагаемые. Сумма 5 есть сумма двух чисел 2 и 3 и в то же время есть объединение пяти единиц, из которых состоят исходные числа 2 и 3.
П р и м е р 1. Пусть эксперимент состоит в подбрасывании 3 монет одновременно. Элементарным исходом будет комбинация из букв О или Р в трёх позициях. В пункте 1.1 было показано, что исходами эксперимента являются восемь следующих исходов
OOO, OOP, OPO, OPP, POO, POP, PPO, PPP.
Можно рассмотреть разнообразные составные явления.
Пусть А = { только на одной монете появляется О }. Это обозначается А = ОРР+РОР+РРО.
Пусть В = { на одной монете появляется Р }.
В = ООР+ОРО+РОО.
События А и В несовместны т. к. если в результате эксперимента только на одной монете появляется орел, то на двух других будет обязательно решка, следовательно результат эксперимента не может быть событием В, так как событие B заключается в том, что только на одной монете появляется решка. Наоборот, если в результате эксперимента только на одной монете появляется решка, то на двух других будет орел и, следовательно результат эксперимента не может быть событием А у которого только на одной монете появляется орёл.
Суммой двух несовместных событий А и В называют событие С, состоящее в появлении события либо А, либо В.
Тогда С = OOP + ОРО + ОРР + РОО +РОР + РРО
Или
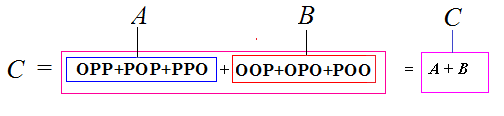
Отсюда видно, что событие С есть сумма элементарных исходов OOO, OOP, … , а с другой стороны сумма двух составных событий А и В. Можно сказать, что сумма двух несовместных составных событий А и В есть объединение элементарных исходов, из которых состоят события А и В. Мы видим, что имеется аналогия между сложением двух натуральных чисел и суммой двух несовместных составных событий.
5.2.Сумма двух совместных событий
Пусть в эксперименте по подбрасыванию трёх монет событие А состоит в том, что ровно на одной из трёх монет появляется О.
А={на одной из трёх монет появляется О} или
А =ОРР+РОР+РРО.
Пусть другое составное событие В состоит из суммы четырёх исходов В = ООР+ОРО+ОРР+РОО. Видно, что события А и В совместны. Если исходом эксперимента является ОРР, то это может рассматриваться как одновременное появление события А и события В.
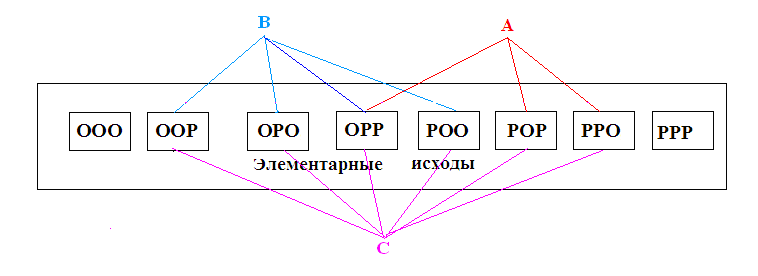
Суммой двух событий А и В называют событие С, состоящее в появлении события либо А, либо В, либо в появлении событий А и В одновременно (С означает, что появится хотя бы одно из событий А или В, или оба вместе).
Согласно определению в данном примере С = ООР + ОРО + ОРР+ РОО + РОР + РРО.
Если результатом бросания трёх монет будет исход ООР или ОРО или РОО, то появляется событие В.
Если результатом бросания трёх монет будет исход РОР или РРО, то появляется событие А.
Если результатом бросания трёх монет будет исход ОРР, то в результате эксперимента появляются одновременно событие А и В.
Несмотря на то, что появление ОРР в эксперименте означает появление двух событий А и В, тем не менее, складывая элементарные исходы из которых состоят события А и В , мы исход ОРР записали в сумму С только один раз.
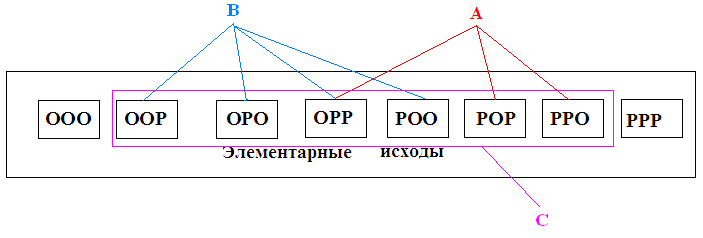
Рис. 5. Событие С есть сумма двух событий А и В т.е. С = А + В. События А и В совместны.