2.4 Верифікація моделі

Тісноту зв'язку між залежною змінною Y та незалежною змінною X оцінюють за допомогою статистичних характеристик: коефіцієнт детермінації, коефіцієнт кореляції. За допомогою цих коефіцієнтів перевіряється відповідність побудованої регресійної моделі (теоретичної) фактичним даним.

У поняття «тіснота зв'язку» вкладається оцінка впливу незалежної змінної (X) на залежну змінну (Y).

Після встановлення тісноти зв'язку між змінними моделі характеризують значимість зв'язку, яка в кореляційному аналізі частіше всього здійснюється за допомогою F-критерію Фішера.

Коефіцієнт детермінації показує, якою мірою варіація залежної змінної (результативного показника) Y визначається варіацією незалежної змінної (вхідного показника) X. Тобто дається відповідь на запитання, чи справді зміна значення Y лінійно залежить саме від зміни значення Х, а не відбувається під впливом різних випадкових факторів. Він використовується як при лінійному, так і при нелінійному зв'язку між змінними та розраховується за формулою:

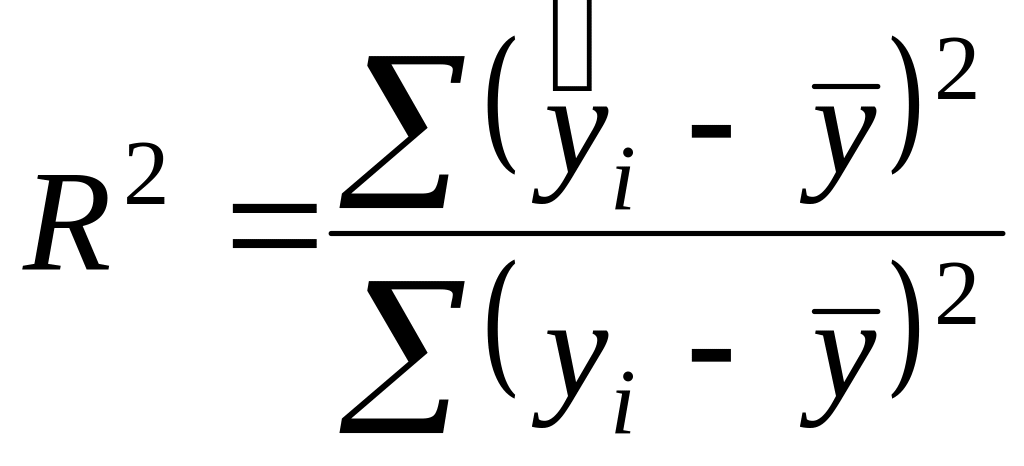(2.14)

де – теоретичні значення залежної змінної на підставі побудованої регресійної моделі;

– загальна середня фактичних даних залежної змінної;

y_i – фактичні індивідуальні значення залежної змінної.

Коефіцієнт детермінації приймає значення від 0 (відсутній лінійний зв'язок між показниками) до 1 (відсутній кореляційний зв'язок між показниками).

Найпростішим критерієм, який дає кількісну оцінку зв’язку між двома показниками, є коефіцієнт кореляції (або індекс кореляції). Він розраховується за такою формулою:

(2.15)

Чим ближче коефіцієнт кореляції до одиниці, тим тісніше зв'язок між незалежною та залежною змінними.

Іноді для спрощення розрахунків тісноту кореляційного зв'язку характеризують коефіцієнтом кореляції, який розраховується за формулою:

(2.16)

Значення R лежить у діапазоні від –1 до +1. При R=0 змінні не можуть мати лінійного кореляційного зв'язку. Ступінь тісноти їх лінійної залежності зростає при наближенні R до ±1. Кореляційний зв'язок між показниками відсутній при R=±1 Коли R>0, то зв'язок між показниками прямий, якщо R<0 – обернений.

В залежності від значення коефіцієнта кореляції зв’язок між перемінними класифікується так:

Значення коефіцієнта кореляції	0	0,1–0,3	0,3–0,5	0,5–0,7	0,7–0,9	0,9–0,99	1
Висновок про силу кореляційного зв’язку	відсутній	слабкий	помірний	середній	високий	досить високий	близький до функціонального

Щоб мати загальне судження про якість моделі із відносних відхилень по кожному спостереженню, визначають середню похибку апроксимації:

(2.17)

Вважається, що середня похибка апроксимація не має перевищувати 8-10%.