1.5 Роль і місце економетричних моделей в математичному моделюванні

Під моделюванням розуміється процес побудови, вивчення і застосування моделей. Воно тісно пов'язане з такими категоріями, як абстракція, аналогія, гіпотеза та ін Процес моделювання обов'язково включає й побудова абстракцій, і умовиводи за аналогією, і конструювання наукових гіпотез. Головна особливість моделювання в тому, що це метод опосередкованого пізнання за допомогою об'єктів-заступників. Модель виступає як своєрідний інструмент пізнання, який дослідник ставить між собою і об'єктом і за допомогою якого вивчає його. Саме ця особливість методу моделювання визначає специфічні форми використання абстракцій, аналогій, гіпотез, інших категорій і методів пізнання.

Можливості моделювання, тобто перенесення результатів, отриманих в ході побудови і дослідження моделі, на оригінал засновані на тому, що модель у певному сенсі відображає (відтворює, моделює, описує, імітує) деякі цікаві для дослідника риси об'єкта.

Математичне моделювання — метод дослідження процесів або явищ шляхом створення їхніх математичних моделей і дослідження цих моделей.

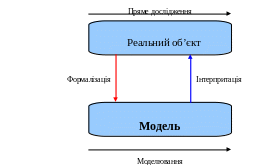
Рисунок 1.8 – Процес моделювання

Формалізація – процес подання інформації про об'єкт, процес, явище в формалізованому вигляді. Формалізація – це метод відображення певної області у вигляді формальної системи, коли форма виділяється у якості особливого предмета дослідження незалежно від змісту. Такий метод полегшує вивчення предмета.

Інтерпретація – це відношення, що переносить формули формальної системи на змінні та зв’язки реальної системи.

До основних проблем економетричного моделювання належать:

• iдентифiкацiя змінних та висування гіпотези про специфiкацiю моделі;

• специфiкацiя економетричної моделі;

• методи оцінювання параметрів моделі;

• верифiкацiя моделі;

• прогноз пояснюваних змінних на основі моделі.

Розв'язання цих проблем значною мірою базується на математично-статистичному iнструментарiї. Велика увага приділяється методам багатовимірного аналізу i, передусім, методам розпізнавання соцiально-економiчних образів, їх типологiзацiї.

Самостійна робота №1 – Приклади економетричних моделей

Виробнича функція Кобба-Дугласа [3, c. 20-24]. Моделі пропозиції і попиту на конкурентному ринку [3, c. 24-26]. Модель Кейнса [3, c. 26-28]. Модель споживання [3, c. 28-30].

Лекція 2.Методи побудови загальної лінійної моделі

Анотація

Загальний вигляд лінійної економетричної моделі, її структура та етапи побудови. Лінійна модель з двома змінними. Передумови застосування методу найменших квадратів (1МНК). Метод найменших квадратів 1МНК. Верифікація моделі. Перевірка значущості та довірчі інтервали. Прогнозування за лінійною моделлю. Методи побудови багатофакторної регресійної моделі. Етапи дослідження загальної лінійної моделі множинної регресії.

2.1 Загальний вигляд лінійної економетричної моделі, її структура та етапи побудови. Лінійна модель з двома змінними.

Модель, що описує кореляційно-регресивний зв’язок між економічними показниками називається загальною, яка дійсна для всієї генеральної сукупності спостережень. У лінійній економетричній моделі має місце лінійний зв’язок між змінними, що характеризують досліджуваний економічний процес чи явище. Зауважимо, що лінійні регресійні моделі є найбільш прості і в переважній більшості випадків – достатні для практики.

У загальному вигляді проста вибіркова регресійна модель запишеться так:

, (2.1)

де Y – вектор спостережень за залежною змінною;

х – вектор спостережень за незалежною змінною;

a₀, а₁ – невідомі параметри регресійної моделі;

u – вектор випадкових величин (помилок).

У загальному матричному вигляді економетрична модель записується так:

(2.2)

де А – матриця параметрів моделі розміром m×n (m – кількість незалежних змінних, n – число спостережень);

Y – матриця значень залежної змінної;

Х – матриця незалежних змінних;

u – матриця випадкової складової.

Регресійна модель називається лінійною, якщо вона лінійна за своїми параметрами. Отже, модель (2.1) є лінійною регресійною моделлю.

Побудова будь-якої економетичної моделі базується на використанні таких специфічних послідовних етапів:

Постановочний етап – визначаються кінцеві цілі дослідження, моделювання, набір факторів та показників, що включаються в модель та їх роль.

Апріорний етап – розробка описувальної моделі, де формулюються та обгрунтовуються показники та система основних припущень.

Етап параметризації та специфікації – розробка математичної моделі досліджуваного об’єкту з вибором методів дослідження, програмного забезпечення ПК або складання алгоритму та програми для ПК за новими задачами.

Інформаційний етап – спостереження і збір необхідної інформації, статистичних даних, їх обробка.

Етап ідентифікації моделі – статистичне оцінювання невідомих параметрів моделі по зібраним даним, статистичний аналіз моделі.

Верифікація моделі – співставлення фактичних, реальних даних і змодельованих, перевірка адекватності моделі, оцінка її точності і прогнозних якостей.

У загальному випадку парна лінійна регресія (з двома змінними)є лінійною функцією між залежною змінною Y і однією пояснюючою змінною Х:

(2.3)

При цьому співвідношення (2.3) називається теоретичною лінійною регресійною моделлю; а₀ і а₁ – теоретичні параметри (коефіцієнти) регресії.

Параметр а₁ (коефіцієнт регресії) — величина іменована, має розмірність результативної ознаки і розглядається як ефект впливу Х на Y. Параметр a₀ — вільний член рівняння регресії, це значення Y при X = 0. Якщо межі варіації X не містять нуля, то цей параметр має лише розрахункове значення.

Щоб визначити значення теоретичних коефіцієнтів регресії, необхідно знати й використовувати всі значення змінних Х і У генеральної сукупності, що практично неможливо. Тому за вибіркою обмеженого обсягу будують так зване емпіричне рівняння регресії, у якому коефіцієнтами є оцінки теоретичних коефіцієнтів регресії:

(2.3)

де â₀, â₁ – оцінки невідомих параметрів а₀ і а₁.

Можливе співвідношення між теоретичним та емпіричним рівнянням регресії схематично зображене на рисунку 2.1.

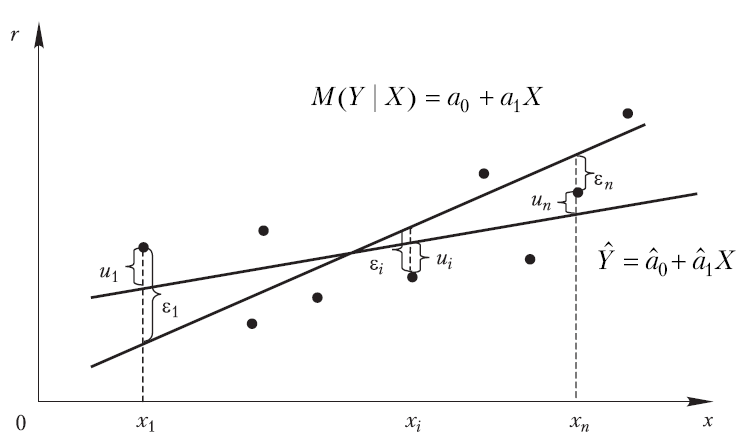
Рисунок 2.1

Найпоширенішим та теоретично обґрунтованим методом визначення коефіцієнтів рівняння регресії є метод найменших квадратів (1 МНК). Оцінки коефіцієнттів регресії, знайдені за методом МНК при визначених передумовах, мають ряд оптимальних властивостей (незміщеність, ефективність, обгрунтованість). Також з даною ціллю використовують такі методи як метод моментів, метод найменших модулів і метод максимальної правдоподібності.