10.4 Оцінювання параметрів авторегресійних моделей

Три авторегресійних моделі – Койка (10.7), адаптивних сподівань (10.8) і часткового коригування (10.9) – можна подати в загальній формі:

. (10.10)

Наявність лагових залежних змінних у динамічних моделях створює певні проблеми при оцінюванні параметрів: серед пояснюючих змінних є стохастичні (залежні лагові змінні), а також існує проблема серійної кореляції залишків моделі та лагових змінних. Залежно від гіпотез щодо залишків таких моделей використовують відповідні методи оцінювання.

Гіпотеза 1. Залишки є нормально розподіленими випадковими величинами з нульовим математичним сподіванням та сталою дисперсією.

Гіпотеза 2. Залишки описуються авторегресійною схемою першого порядку:

. (10.11)

Гіпотеза 3. Залишки автокорельовані та описуються авторегресійною схемою першого порядку:

, (10.12)

крім того, .

Перша гіпотеза виконується лише для моделі часткового коригування (10.9); саме для неї можливе застосування звичайного МНК. Однак залежність залишків від лагової змінної у цій моделі призводить до зміщення оцінок параметрів. Та хоча оцінки параметрів будуть завищеними, вони матимуть найменшу середньоквадратичну похибку. І після визначення величини зміщення МНК-оцінки будуть найприйнятнішими.

Якщо залишки моделі визначаються через автокорельовані випадкові величини, то МНК-оцінки параметрів моделі також матимуть зміщення, до того ж зміщення матиме також критерій Дарбіна-Уотсона. Тому для перевірки автокореляції залишків застосовують узагальнений критерій Дарбіна-Уотсона. Оцінювання параметрів таких моделей виконують узагальненим методом найменших квадратів (методом Ейткена), в операторі оцінювання якого

(10.13)

коригуюча матриця має вигляд:

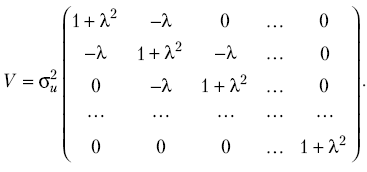(10.14)

Якщо лагову модель можна подати у вигляді

, (10.15)

то до перетворених у такий спосіб даних залежної змінної застосовують звичайний МНК. Причому параметр  вибирають з інтервалу так, щоб мінімізувати суму квадратів залишків .

Якщо відносно залишків моделі приймається третя гіпотеза, то параметри оцінюють за допомогою таких методів:

1. класичного МНК після попереднього перетворення вхідних даних;

2. методу Ейткена (узагальненого МНК);

3. ітераційного методу;

4. методу інструментальних змінних;

5. алгоритму Уолліса.

10.5 Виявлення автокореляції залишків в авторегресійних моделях

Автокореляцію в авторегресійних моделях практично неможливо визначити за допомогою статистики DW Дарбіна-Уотсона, так як для цих моделей значення DW навіть за наявності автокореляції близьке до 2, що за критерієм Дарбіна-Уотсона рівносильне відсутності автокореляції.

Для виявлення автокореляції в авторегресійних моделях Дарбін запропонував використовувати h-статистику, що має вигляд:

, (10.16)

де n – об’єм вибірки;

D(g) — дисперсія оцінки коефіцієнта при лаговій змінній y_t-1;

— оцінка коефіцієнта автокореляції першого порядку, яку можна визначити на основі формули:

(10.17)

Схема використання h-статистики для аналізу автокореляції має такі особливості використання:

• незалежно від того, скільки лагів змінної y включено в модель, значення h необхідно обчислювати з використанням дисперсії коефіцієнта при y_t-1;

• статистика h не обчислюється, якщо 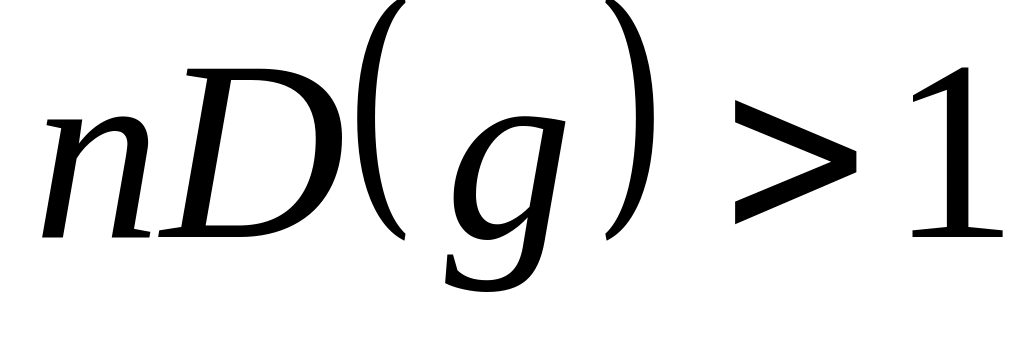(на практиці такі ситуації майже не зустрічаються);

• застосування h доцільно лише при досить великому обсязі вибірки n.

Як зазначалося раніше, автокореляція залишків призводить до отримання зміщених і неефективних оцінок. Автокореляція може вказувати або на невірну специфікацію рівняння, або на наявність важливих неврахованих факторів. Але часто автокореляція викликається наявністю регресійної залежності між відхиленнями, тобто внутрішніми властивостями ряду {_t}. Існує кілька способів усунення даної проблеми. Зокрема, для авторегресійних моделей пропонуються авторегресійне перетворення, перетворення методом ковзних середніх, моделі ARMA і ARIMA.