4.2 Методи визначення гетероскедастичності

Як і в разі мультиколінеарності, єдиних правил виявлення гетероскедастичності немає, а є різноманітні тести (критерії): аналіз змісту проблеми, графічний аналіз, тест рангової кореляції Спірмена, тест Гейзера, критерій , параметричний та непараметричний тести Гольдфельда-Квандта, тест Глейзера, тест рангової кореляції Спірмана та ін. Розглянемо деякі з них.

1. Аналіз змісту проблеми.

Інколи при проведенні економетричних досліджень гетероскедастичність вгадується інтуїтивно або висувається як абсолютне припущення. Попередній аналіз проблеми, що вивчається, може навести на думку про наявність гетероскедастичності. Наприклад, при вивченні бюджету сім'ї можна помітити, що дисперсія залишків зростає відповідно до зростання доходу. При зведеному аналізі діяльності різних за розміром фірм також можна очікувати гетероскедастичність. І таких прикладів багато. Отже, перший крок до вияву гетероскедастичності — глибокий аналіз досліджуваної проблеми.

2. Графічний аналіз

Досить наочним та простим методом тестування припущення про наявність гетероскедастичності є графічний метод. Не завжди дослідник володіє необхідним для аналізу проблеми емпіричним матеріалом. Крім того, його висновки щодо наявності або відсутності гетероскедастичності носять суб'єктивний характер, і в цих умовах на допомогу приходять графіки.

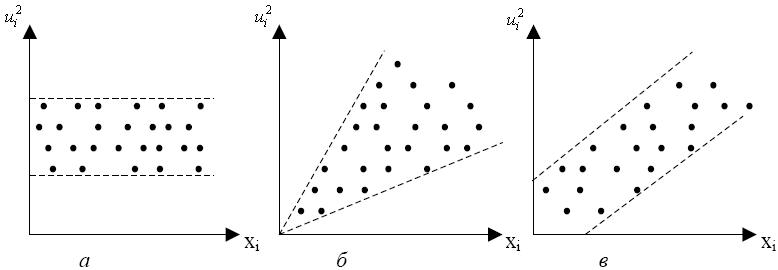
Рисунок 5.5 – Різні типи графіків квадрату залишків

3. Тест рангової кореляції Спірмена

Це найпростіший тест, який можна використовувати як до малих, так і до великих вибірок.

Спочатку запишемо коефіцієнт рангової кореляції Спірмана:

(5.1)

де – різниця рангів кожної пари значень;

n – число спостережень.

Наведений коефіцієнт рангової кореляції може використовуватись для визначення гетероскедастичності таким чином.

Припустимо, .

Етап 1. Побудувати регресію для даних у та х і розрахувати відхилення u_i.

Етап 2. Нехтуючи знаком u_i, тобто беручи абсолютні значення | u_i |, ранжуємо | u_i | та х_i у зростаючому чи спадному порядку і підрахуємо коефіцієнт рангової кореляції Спірмана.

Етап 3. Перевіряємо значимість отриманого коефіцієнта рангової кореляції за t–критерієм Ст'юдента. Для цього побудуємо t-статистику:

. (5.2)

При даних ступенях вільності за таблицями Ст'юдента знаходимо t. Якщо розраховане значення перевищує t_кр (t > t_кр), це підтверджує гіпотезу про гетероскедастичність. Якщо t ≤ t_кр, тоді в регресійній моделі правильним є припущення про гомоскедастичність.

4. Тест Глейзера.

Розглянемо його алгоритм на прикладі простої лінійної регресії.

Етап 1. Знаходимо невідомі параметри простої лінійної регресії методом найменших квадратів та обчислюємо помилки u_i для кожного окремого спостереження.

Етап 2. Будуємо регресію, яка пов'язує абсолютні значення знайдених на першому етапі помилок (|u_i|) з незалежною змінною х. Ми беремо абсолютні значення помилок, а не їхні справжні значення, бо Σu_i = 0 , і тому не можливо буде підібрати регресію u = f(x). Фактична форма цієї регресії звичайно не відома, тому до неї можна підбирати різні форми кривих. Глейзер пропонував такі залежності:

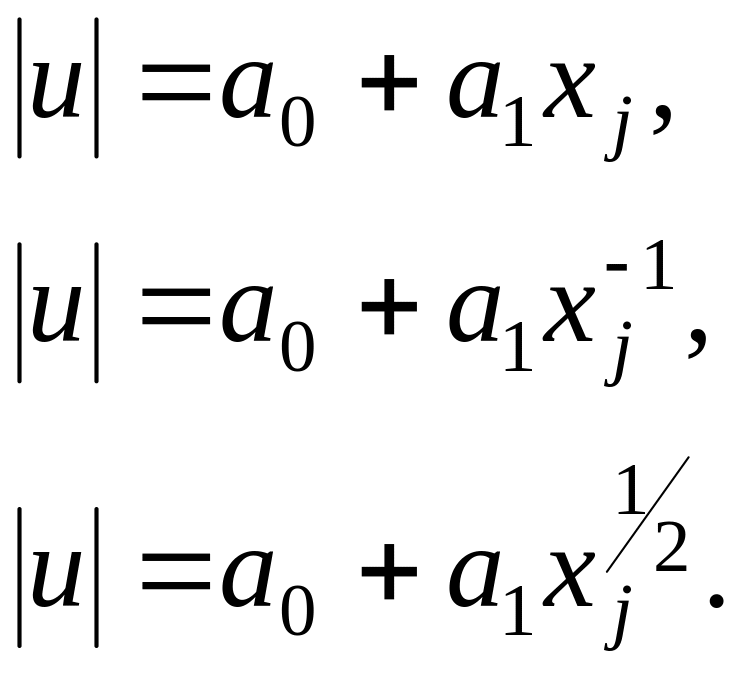
Обираємо ту регресію, яка найкраще підходить з огляду на коефіцієнт кореляції та середні квадратичні відхилення параметрів а₀ та а₁. (Зверніть увагу, що коли а₀ = 0 та а₁ ≠ 0, така ситуація називається «чиста гетероскедастичність»; якщо а₀ та а₁ ≠ 0, цей випадок називається «змішана гетероскедастичність»).

Гетероскедастичність визначається в світлі статистичної значимості параметрів а₀ та а₁, тобто ми виконуємо будь-який стандартний тест перевірки на значимість параметрів, і якщо вони значно відрізняються від нуля, то u_i, є гетероскедастичними.

Перевага тесту Глейзера в тому, що він дає також інформацію про форму гетероскедастичності, тобто про спосіб, яким пов'язані u_i та х. Ця інформація є важливою для «корекції» гетероскедастичності.

Зазначимо, що у разі багатофакторної регресії на етапі 1 знаходимо помилки u_i для регресії, що вміщує всі фактори. На етапі 2 будуємо залежності між абсолютними величинами знайдених помилок та залежною змінною у.

Слід зазначити, що деякі статистики надають перевагу тестам рангової кореляції Спірмана і Гольдфельда – Квандта перед тестом Глейзера для визначення гетероскедастичності. Якщо якимось із цих тестів виявлено гетероскедастичність, тоді можна експериментувати з функцією Глейзера з метою вирішення, які зміни початкових даних необхідні, щоб подолати гетероскедастичність.

5. Параметричний тест Гольдфельда – Кванта

Цей тест застосовується до великих вибірок. Спостережень має бути хоча б удвічі більше, ніж оцінюваних параметрів. Тест припускає нормальний розподіл та незалежність випадкової величини u_i.

1-ий крок: спостереження (вихідні дані) впорядкувати відповідно до величини елементів вектора х_i, який може спричинити зміну дисперсії залишків.

2-ий крок: відкинути с спостережень, які розміщені всередині векторів вихідних даних, де , n – кількість елементів вектора х_i..

3-ий крок: побудувати дві моделі на основі звичайного МНК за двома створеними сукупностями спостережень обсягом за умови, що , де m – кількість змінних.

4-ий крок: знайти суму квадратів залишків S₁ і S₂ за першою і другою моделями:

, (5.3)

де u₁, u₂ – залишки відповідно за першою і другою моделями.

5-ий крок: розрахувати критерій (якщо S₂ > S₁), який у разі виконання гіпотези про гомоскедастичність відповідатиме F-розподілу з , ступенями свободи; Значення критерію F^* порівняти з табличним значенням F-критерію при вибраному рівні значущості  і відповідних ступенях свободи. Якщо , то гетероскедастичність відсутня.

Чим більше значення F^*, тим більша гетероскедастичність залишків.

Цей тест може бути використаний при припущенні про обернену пропорційність між σ_і і значеннями пояснюючої змінної. При цьому статистика Фішера має вид: .

6. Непараметричний тест Гольдфельда – Квандта

Цей тест базується на встановленні кількості піків значень залишків після впорядкування (ранжування) спостережень за х_ij . Якщо для всіх значень змінної х_ij залишки розподіляються приблизно однаково, то дисперсія їх однорідна і гетероскедастичність відсутня. Якщо вона змінюється, то гетероскедастичність присутня.

Зазначимо, що цей тест не цілком надійний для перевірки на гетероскедастичність. Однак він дуже простий і часто використовується для першої оцінки наявності гетероскедастичності множини спостережень.