Лекція 5.Узагальнений метод найменших квадратів

Анотація

Поняття гомо- і гетероскедастичності. Вплив гетероскедастичності на властивості оцінок параметрів. Методи визначення гетероскедастичності. Усунення гетероскедастичності трансформуванням початкової моделі. Узагальнений метод найменших квадратів (метод Ейткена) оцінок параметрів лінійної економетричної моделі з гетероскедастичними залишками. Прогноз за моделлю.

4.1 Поняття гомо- і гетероскедастичності. Вплив гетероскедастичності на властивості оцінок параметрів

Одним з основних припущень моделі класичної лінійної регресії є припущення про сталість дисперсії кожної випадкової величини u_i (гомоскедастичність).

Формалізовано це припущення записується у вигляді:

Якщо це припущення не задовольняється в якомусь окремому випадку, то

Має місце гетероскедастичність. Звичайно нас цікавить питання про доцільність цього припущення і про те, що відбувається, коли припущення про сталість дисперсії випадкової величини u_i не задовольняється.

Суть припущення гомоскедастичності полягає в тому, що варіація кожної u_i навколо її математичного сподівання не залежить від значення х. Дисперсія кожної u_i. зберігається сталою незалежно від малих чи великих значень факторів: не є функцією х_ij тобто .

Графічно випадок гомоскедастичності для простої лінійної регресії показано випадковою дисперсією u_i у межах сталої відстані навколо лінії регресії (див. рис. 5.1).

Рисунок 5.1 – Гомоскедастичність

Якщо не є сталою, а її значення залежать від значень х, можемо записати

У цьому разі маємо справу з гетероскедастичністю.

Графічна форма розкиду спостережень залежить від форми гетероскедастичності, тобто форми зв'язку між та х_i На рисунку 5.2-5.4 показано три різні форми гетероскедастичності.

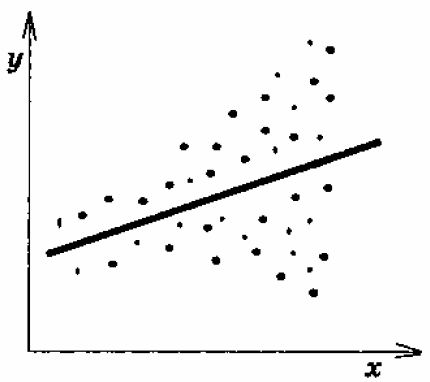
Рисунок 5.2 – Зростання дисперсії u_i

Зокрема на рис. 5.2 показано випадок (монотонно) зростаючої дисперсії (із зростанням х зростає і дисперсія u_i).

Це загальноприйнята форма гетероскедастичності, що допускається в економетричних дослідженнях. На рис. 5.3 показано випадок спадної гетероскедастичності: коли х набуває більших значень, відхилення спостережень від лінії регресії зменшується, таким чином дисперсія випадкової змінної зменшується із зростанням х.

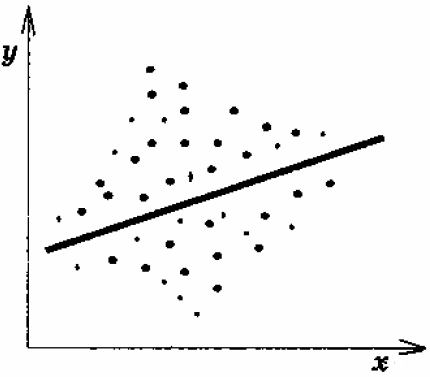
Рисунок 5.3 – Спадання дисперсії u_i

На рис. 5.4 зображено більш складну форму гетероскедастичності: спочатку дисперсія є зменшується із зростанням х, але після певного рівня х* починає зростати із зростанням х.

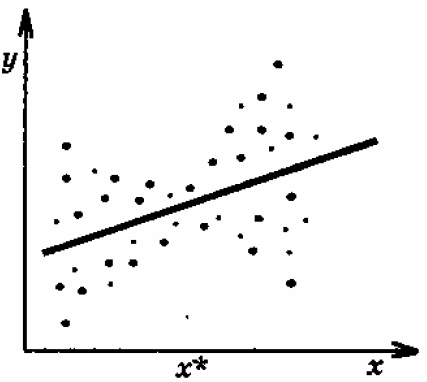
Рисунок 5.4 – Складний випадок

Форма гетероскедастичності залежить від знаків та значень коефіцієнтів у залежності Оскільки u_i – неспостережувана випадкова величина, ми не знаємо справжньої форми гетероскедастичності.

У прикладних дослідженнях, як правило, використовується зручне припущення, що гетероскедастичність (у разі простої лінійної регресії) має форму , де k — константа, яку потрібно оцінити.

У багатьох економетричних дослідженнях може очікуватись, що припущення про сталу дисперсію випадкової змінної не зберігатиметься. Це можна легко зрозуміти, якщо врахувати фактори, вплив яких абсорбується значенням помилки. Згадаємо, що випадкова величина u_i виражає вплив на залежну змінну помилок в її вимірюванні та неврахованих факторів. У обох випадках є підстави для зміни з часом дисперсії u_i. Помилки вимірювання мають тенденцію до накопичення з плином часу, тому їхня величина збільшується. У такому разі дисперсія u_i збільшується із зростанням значень х. З іншого боку, техніка вибірки та інші методи збору даних постійно вдосконалюються і тому похибки вимірювання можуть зменшуватися. У такому разі також зменшуватиметься. Але важливіше те, що багато із неврахованих змінних можуть змінюватись в однаковому з х напрямку, викликаючи, таким чином, збільшення відхилення спостережень від лінії регресії.

Наслідки порушення припущення про гомоскедастичність:

1. неможливо знайти середньоквадратичне відхилення параметрів 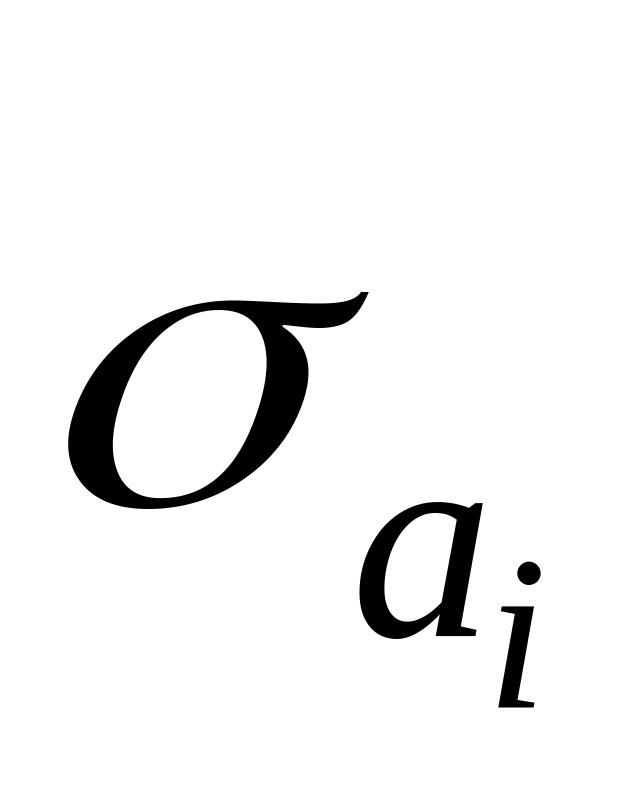регресії, а отже, неможливо оцінити значущість параметрів;

2. неможливо побудувати довірчий інтервал для прогнозних значень y_р ;

3. отримані за МНК оцінки параметрів регресії не є ефективними (не мають найменшої дисперсії).

Зазначимо, що якщо незважаючи на гетероскедастичність ми використовуватимемо звичайні процедури перевірки гіпотез, то висновки можуть бути неправильними. Тому оцінки параметрів доцільно знаходити за узагальненим методом найменших квадратів (інша назва – метод Ейткена).