4.3 Критерії відмінності між групами (незалежні вибірки)

Незв'язані або незалежні вибірки утворюються, коли з метою експерименту для порівняння залучаються дані двох або більше вибірок, причому ці вибірки можуть бути взяті із різних генеральних сукупностей. Таким чином, для незв'язаних вибірок характерно, що в них обов'язково входять різні випробовування.

Для оцінки достовірності відмінностей між незв'язними вибірками використовується ряд непараметричних критеріїв: критерій серій Вальда-Вольфовица, U критерій Манна-Уітні та двохвибірковий критерій Колмогорова-Смирнова.. Одним з найбільш поширених є критерій U – Вилкоксона (Манна – Уітні).

Критерій U – застосовують для оцінки відмінностей за рівнем вираженості якої-небудь ознаки для двох незалежних (незв'язних) вибірок. При цьому вибірки можуть розрізнятися за кількістю вхідних досліджуваних об’єктів. Цей критерій особливо зручний у тому випадку, коли кількість досліджуваних об’єктів невелика і в обох вибірках не перевищує число 20, хоча таблиці критичних значень розраховані для величин вибірок, що не перевищують 60 піддослідних об’єктів.

Для застосування U – критерію Манна Уітні потрібно провести наступні операції:

1. Побудувати єдиний рангований ряд з обох співставлюваних вибірок, розставляючи елементи за ступенем збільшення ознаки і приписати меншому значенню менший ранг. Загальна кількість рангів буде рівна:

(4.1)

де n₁ – кількість одиниць в першій вибірці;

n₂ – кількість одиниць в другій вибірці.

2. Розділити єдиний рангований ряд на два, які складаються із елементів першої і другої вибірок відповідно. Підрахувати окремо суму рангів, що припадають на долю елементів першої вибірки, і окремо – на долю елементів другої вибірки. Визначити більшу із двох рангових сум (T_x), що відповідає вибірці з n_x одиниць.

3. Визначити значення U – критерію Манна – Уітні за формулою:

(4.2)

4. По таблиці для вибраного рівня значимості визначити критичне значення для даних n₁ та n₂. Якщо отримане значення U менше табличного чи рівне йому, то признається наявність суттєвої різниці між рівнем ознаки в досліджуваних вибірках. Якщо отримане значення більше табличного, приймається протилежна гіпотеза. Достовірність розбіжностей тим вища, чим менше значення U.

Приклад 4.1: Дві нерівні за чисельністю групи студентів працювали над проектом. Показником успішності виступав час вирішення (див. таблицю 1). Студенти меншої за чисельністю групи отримували додаткову мотивацію у вигляді грошової винагороди. Чи впливає винагорода на успішність виконання завдання?

Таблиця 4.1 – Початкові дані

Група з додатковою мотивацією	32	35	44	8	25	25	30	43
Група без мотивації	46	8	50	45	32	41	40	31	54

Число піддослідних у вперше групі позначається як n₁ і дорівнює 8, по – другий як n₂ і дорівнює 9.

Для відповіді на питання завдання застосуємо критерій U – Вілкоксона – Манна – Уітні.

Отримані дані необхідно об'єднати, тобто представити як один ряд і впорядкувати його за зростанням величин, що в нього входять. Підкреслимо, що для критерію U важливі не самі чисельні значення даних, а порядок їх розташування. Попередньо позначимо кожен елемент першої групи символом х, а другий – символом у. Тоді загальний упорядкований за зростанням чисельних величин ряд можна представити так:

X Y X X X Y X Y X Y Y X X Y Y Y Y

8 8 25 25 30 31 32 32 35 40 41 43 44 45 46 50 54

Побудувати єдиний рангований ряд з обох співставлюваних вибірок, розставляючи елементи за ступенем збільшення ознаки і приписати меншому значенню менший ранг. Загальна кількість рангів буде рівна:

Ряд	8	8	25	25	30	31	32	32	35	40	41	43	44	45	46	50	54
Ранг	1,5	1,5	3,5	3,5	5	6	7,5	7,5	9	10	11	12	13	14	15	16	17

Розділимо єдиний рангований ряд на два, які складаються із елементів першої і другої вибірок відповідно. Підрахуємо окремо суму рангів, що припадають на долю елементів першої вибірки, і окремо – на долю елементів другої вибірки.

Х	Ранг Х	Y	Ранг Y
8	1,5	35	9
8	1,5	40	10
25	3,5	41	11
25	3,5	43	12
30	5	44	13
31	6	45	14
32	7,5	46	15
32	7,5	50	16
		54	17
Суми	55		98

Звідси визначаємо найбільшу з рангових сум: .

Визначаємо значення U – критерію Манна – Уітні за формулою:

.

Отримавши U звертаємося до статистичної таблиці. Ця таблиця складається з декількох таблиць, розрахованих окремо для рівнів Р = 0,05, P = 0,01, а також для величин n₁ і n₂. У нашому випадку n₁ = 8 і n₂ = 9. За цими таблицями знаходимо, що значення рівні:

15 для ,

9 для .

Відповідна «вісь значимості» має вигляд:

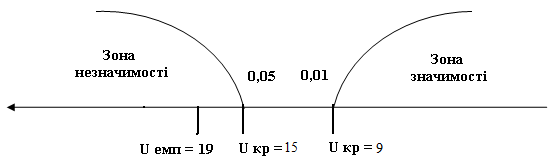
Отримане значення U_ЕМП потрапило в зону незначущості, отже, приймається гіпотеза про подібність, а гіпотеза про наявність відмінностей відхиляється. Таким чином, психолог може стверджувати, що додаткова мотивація не приводить до статистично значимого збільшення ефективності рішення технічної задачі.

Для застосування критерію U необхідно дотримуватися таких умов:

• Вимірювання повинно бути вироблено в шкалі інтервалів і відносин.

• Вибірки мають бути незв'язаними.

• Нижня межа застосовності критерію n₁ ≥ 3 і n₂ ≥ 3 або n₁ = 2, а n₂ ≥ 5.

• Верхня межа застосовності критерію: n₁ і n₂ ≤ 60.

Критерій серій Вальда-Вольфовіца

Найбільш часто в нульовій гіпотезі формулюється твердження відносно конкретного параметру чи параметрів, наприклад, середнього значення, медіани, стандартного відхилення, дисперсії. Однак в деяких випадках нас цікавлять більш загальні нульові гіпотези, що стосуються любих відмінностей між генеральними сукупностями.

При невеликому об’ємі вибірки (n₁ ≤ 20 і n₂ ≤ 20):

Умова
А	В
26	16
22	10
19	8
21	13
14	19
18	11
29	7
17	13
11	9
34	21

1. Об’єднуємо значення обох вибірок і розташовуємо їх в порядку спадання.

Відмітка	Умова
34	А
29	А
26	А
22	А
21	А
21	В
19	В
19	А
18	А
17	А
16	В
14	А
13	В
13	В
11	В
11	А
10	В
9	В
8	В
7	В

2. Розміщуємо ідентифікатори кожної з умов в горизонтальному положенні, підкреслюємо кожну серію в об’єднаній вибірці і підраховуємо загальну кількість серій.

ААААА ВВ ААА В А ВВВ А ВВВВ

3. Якщо співпадають між собою відмітки для різних умов, то послідовність залишається без змін, але якщо співпадають відмітки для різних умов, то можливе отримання більш чим однієї послідовності. В цьому випадку рекомендується визначити шляхом перебору всі можливі послідовності і знайти число серій для кожної з них. Якщо всі вони виявляться статистично значимими, то гіпотеза може бути відхилена.

ААААА ВВ ААА В А ВВВ А ВВВВ, R = 8;

ААААА В А В АА В А ВВВ А ВВВВ, R = 10;

ААААА ВВ ААА В А ВВ А ВВВВВ, R = 8;

ААААА В А В АА В А ВВ А ВВВВВ, R = 10;

АААА В А В ААА В А ВВВ А ВВВВ, R = 10;

АААА В АА В АА В А ВВВ А ВВВВ, R = 10;

АААА ВВВ ААА В А ВВ А ВВВВВ, R = 8;

АААА ВВ А В АА В А ВВ А ВВВВВ, R = 10.

4. Визначаємо критичне значення R (число серій) для n₁ = 10 і n₂ = 10. При використанні критерію серій для двох вибірок нас цікавить нижнє значення R, що відповідає різним значенням n₁ та n₂.

5. Для випадку, коли одні значення R значимі, а інші ні, не існує задовільного способу прийти до статистичного рішення. Один з запропонованих методів полягає в знаходженні ймовірностей, що асоціюються з кожним R, і в подальшому визначенні середнього значення. Якщо воно вийде меншим за α, чи рівним йому, то гіпотеза буде відхилена.

При великих об’ємах вибірок (n₁ > 20 і n₂ > 20):

Оскільки табличне значення критерію серій не виходить за межі n₁ чи n₂ = 20, всякий раз, коли об’єм вибірки для якоїсь з групп перевищує 20 можна застосувати альтернативну процедуру. При цьому значення ймовірності для R може бути апроксимоване за допомогою z-перетворення, причому z інтерпретується як змінна стандартного нормального закону розподілу. Z-перетворення має вигляд:

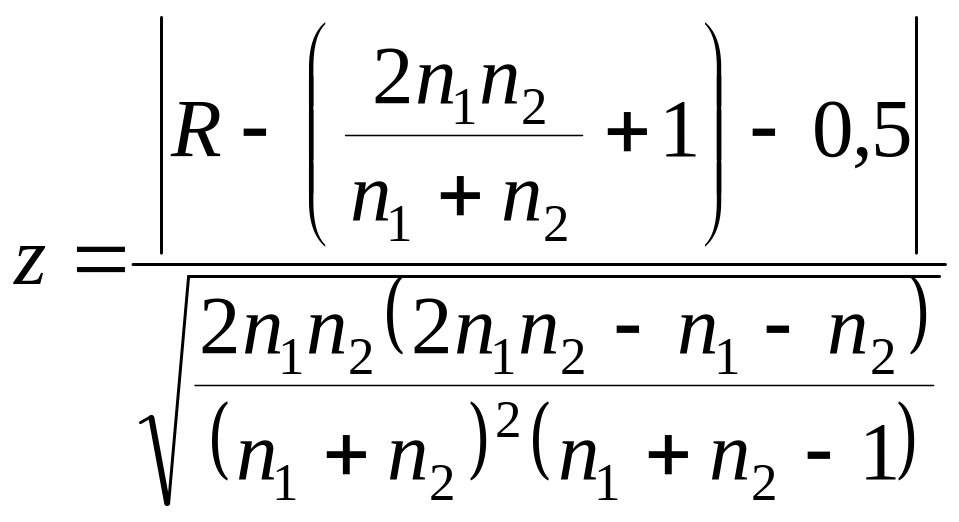, (4.3)

де 0,5 вираховується із абсолютної величини чисельника для поправки на непервність.