Понятие о среднем, средневыпрямленном и действующем значении гармонических токов и напряжений

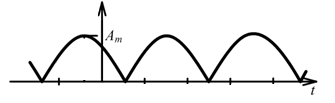
Среднее значение периодической функции а (t) за период:

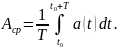
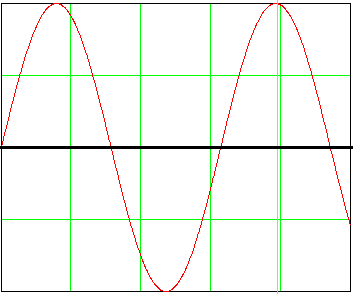
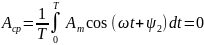
0

Средневыпрямленным значением периодической функции называется среднее значение модуля функции:

[Введите цитату из документа или краткое описание интересного события. Надпись можно поместить в любое место документа. Для изменения форматирования надписи, содержащей броские цитаты, используйте вкладку "Работа с надписями".]

A_{ср. в}

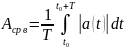
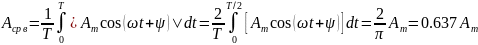, В, А и т. д.

Действующим значением периодического тока или напряжения называется среднеквадратическое значение этой функции.

.

=

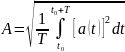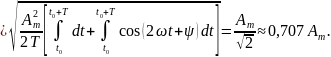
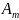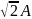
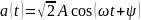
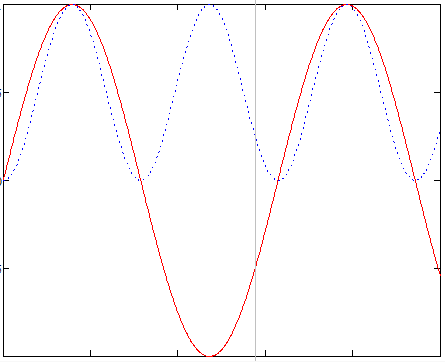
0.707

Средняя мощность на них для постоянных токов:

.

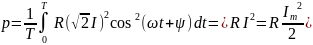Обозначение электрических физических величин

Мгновенные значения	Действующие значения	Амплитудные значения	Размерность
i(t)	I	Im	А
u(t)	U	Um	В
e(t)	E	Em	В
j(t)	J	Jm	А

В общем случае для анализа цепи, находящейся под гармоническим воздействием, необходимо решить дифференциальное уравнение вида:

.

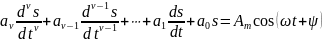Классические методы решения данного дифференциального уравнения очень сложны.

Метод комплексных амплитуд

В установившемся режиме токи и напряжения всех ветвей линейной цепи, находящейся под гармоническим воздействием, являются гармоническими функциями времени той же частоты, и, следовательно, задача анализа цепи состоит в нахождении начальных фаз и амплитуд необходимых токов и напряжений.

Метод комплексных амплитуд относится к символическим методам, основанным на преобразовании исходных функций, называемых оригиналами, в другие функции, называемых изображениями или символами.

При этом операции над исходными функциями заменяются более простыми операциями над изображениями.

Таким образом, символические методы содержат три этапа:

1. прямое преобразование от оригиналов к изображениям;

2. определение изображений искомых величин;

3. обратное преобразование от изображений к оригиналам.

Метод комплексных амплитуд основан на представлении гармонических функций времени с помощью комплексных чисел.

Комплексным числом А называется выражение вида

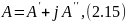
где А', А" — действительные числа, называемые, соответственно, вещественной и мнимой составляющими комплексного числа; 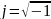— мнимая единица.

Изображение вещественного числа на числовой оси:

0 1 2 3 n

И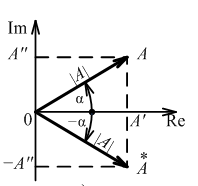 зображение комплексного числа в Декартовой системе координат

,

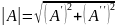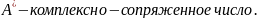
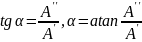
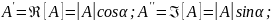
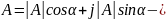тригонометрическая функция Эйлера

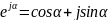
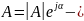показательная форма записи комплексного числа

Комплексно – сопряженные числа:

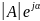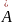A = A' + jA''= ; = A' − jA''= .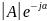

Операции сложения и вычитания лучше делать в алгебраической форме:

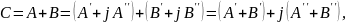
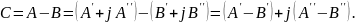
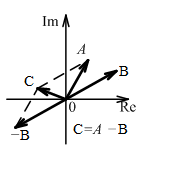
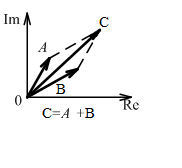
Сумма двух сопряженных чисел:

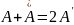
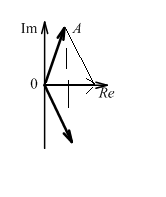
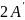
Умножение и деление комплексных чисел можно производить также и в показательной форме:

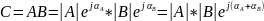
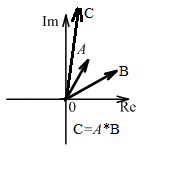
Деление:

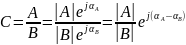
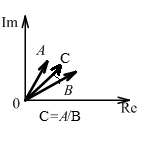
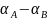
Возведение в степень:

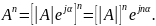
Умножение на число:

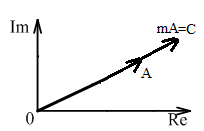
При умножении на 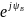осуществляется поворот вектора A на угол .

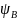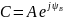
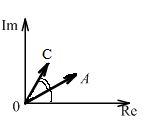
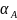
Умножение вектора  А = 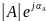на вектор

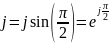равносильно повороту вектора А на угол π/2 против часовой стрелки:

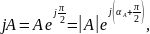
а умножение вектора  А на вектор

приводит к повороту вектора  А на угол π/2 по часовой стрелке: