- •Лекция 1
- •1.1. Основные определения Электрическая цепь
- •Электрический ток
- •Напряжение
- •Мощность и энергия
- •Схемы электрической цепи
- •Идеализированные пассивные элементы Резистивный элемент
- •Вольт-амперная характеристики резистора с линейным сопротивлением
- •Лекция 2 Емкостный элемент
- •Индуктивный элемент
- •Закон электромагнитной индукции:
- •Дуальные элементы цепи
- •Идеализированные активные элементы
- •Идеальный источник тока
- •Схемы замещения реальных источников
- •Управляемые источники тока и напряжения
- •Компонентные и топологические уравнения Законы Кирхгофа
- •Графы схем электрических цепей
- •Определение числа независимых узлов и контуров.
- •Основные задачи теории цепей
- •Понятие об уравнениях электрического равновесия
- •Лекция 4 Линейные электрические цепи при гармоническом воздействии
- •Понятие о среднем, средневыпрямленном и действующем значении гармонических токов и напряжений
- •Метод комплексных амплитуд
- •Комплексные изображения гармонических функций времени
- •Операции над комплексными изображениями гармонических функций
- •Лекция 5
- •Комплексная схема замещения цепи. Законы Ома и Кирхгофа в комплексной форме
- •Порядок анализа цепи методом комплексных амплитуд
- •Идеализированные пассивные элементы при гармоническом воздействии Резистивный элемент
- •Емкостный элемент
- •Индуктивный элемент
- •Лекция 6 Анализ простейших линейных цепей при гармоническом воздействии Последовательная rl-цепь
- •Последовательная rc – цепь
- •Последовательная rlc – цепь
- •Параллельная rlc – цепь
- •Делители напряжения и тока Делитель напряжения
- •Лекция 7 Энергетические процессы в простейших цепях при гармоническом воздействии Аналогии между механическими и электромагнитными процессами
- •Мгновенная мощность пассивного двухполюсника при гармоническом воздействии.
- •Активная, реактивная, полная и комплексная мощности
- •Баланс мощностей
- •Согласование источника энергии с нагрузкой
- •Лекция 8 Преобразования электрических цепей
- •Участки цепей с последовательным соединением элементов
- •Участки цепей с параллельным соединением элементов
- •Участки цепей со смешанным соединением элементов
- •Эквивалентное преобразование треугольника сопротивлений в звезду и обратное (самостоятельно)
- •Последовательная и параллельная схемы замещения пассивного двухполюсника
- •Перенос источников
- •Лекция 9 Цепи с взаимной индуктивностью
- •Понятие об одноименных зажимах
- •Коэффициент связи между индуктивными катушками
- •Цепи с взаимной индуктивностью при гармоническом воздействии
- •Эквивалентные преобразования участков цепей со связанными индуктивностями
- •Понятие о линейных трансформаторах
- •Лекция 10 Комплексные частотные характеристики линейных электрических цепей Понятие о комплексных частотных характеристиках
- •Комплексные частотные характеристики идеализированных двухполюсных пассивных элементов
- •Кчх цепей с одним реактивным элементом
- •Комплексный коэффициент передачи по напряжению
- •Логарифмические ачх и фчх
- •Лекция 11 Последовательный колебательный контур
- •Резонансная частота, характеристическое сопротивление и добротность контура
- •Энергетические процессы в последовательном колебательном контуре
- •Комплексные частотные характеристики
- •Передаточные характеристики контура
- •Лекция 12 Параллельный колебательный контур
- •Параллельный колебательный контур с разделенной индуктивностью
- •П араллельный колебательный контур с разделенной емкостью
- •Лекция 13 Методы формирования уравнений электрического равновесия цепи
- •Метод контурных токов (кт)
- •Метод узловых напряжений
- •Формирование уравнений электрического равновесия цепей с зависимыми источниками
- •Лекция 14 Основные теоремы теории цепей Принцип наложения (суперпозиции)
- •Теорема взаимности (обратимости)
- •Теорема компенсации
- •Теорема об эквивалентном источнике
- •Лекция 15 Многополюсники и цепи с многополюсными элементами
- •Классификация и схемы включения многополюсников
- •Основные уравнения и первичные параметры линейных неавтономных многополюсников
- •Основные уравнения и системы первичных параметров проходных четырехполюсников Классификация проходных четырехполюсников
- •Основные уравнения и основные параметры неавтономных проходных четырехполюсников
- •Методы определения первичных параметров четырехполюсников
- •Лекция 16 Первичные параметры составных четырехполюсников
- •Схемы замещения неавтономных проходных четырехполюсников
- •Автономные проходные четырехполюсники
- •Характеристические параметры и комплексные частотные характеристики (кчх) неавтономных проходных четырехполюсников к чх четырехполюсников при произвольной нагрузке
- •Характеристические сопротивления неавтономного проходного четырехполюсника
- •Характеристические постоянные передачи неавтономного проходного четырехполюсника
Определение числа независимых узлов и контуров.
Число независимых узлов равно m = q – 1.
Для составления системы независимых уравнений баланса токов выбирают узлы с номерами от 1 до q – 1. Узел (0) называют базисным.
Число независимых контуров определяется числом главных ветвей n = p − q + 1. Поэтому число независимых уравнений баланса напряжений равно n.
Общее число линейно независимых уравнений на основании законов Кирхгофа:
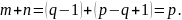
Основные задачи теории цепей
Л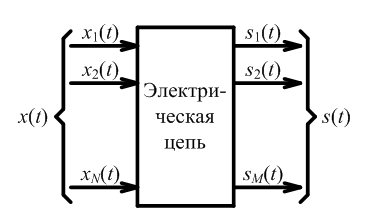 юбую
электрическую цепь можно рассматривать
как систему с одним или несколькими
входами и одним или несколькими выходами
(рис. 1.37). Если к входам цепи подать
внешнее воздействие в виде независимых
источников токов и напряжений, то на
выходах появятся отклики, также в виде
токов и напряжений.
юбую
электрическую цепь можно рассматривать
как систему с одним или несколькими
входами и одним или несколькими выходами
(рис. 1.37). Если к входам цепи подать
внешнее воздействие в виде независимых
источников токов и напряжений, то на
выходах появятся отклики, также в виде
токов и напряжений.
Задачи теории цепей:
Анализ цепи состоит в определении реакции цепи в виде токов и напряжений на всех или отдельных элементах цепи на заданное внешнее воздействие.
Синтез цепи состоит в определении структуры и параметров элементов цепи по заданному воздействию и отклику.
В
частном случае задачи синтеза могут
сводиться к нахождению соотношений
между реакцией
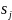 на воздействие
на воздействие
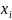 .
Такие соотношения называются
характеристиками цепи.
.
Такие соотношения называются
характеристиками цепи.
Определение и исследование частотных характеристик – это задача анализа цепи в частотной области.
Нахождение временных характеристик — это задача анализа цепи во временной области.
Понятие об уравнениях электрического равновесия
Математически задача анализа электрической цепи сводится к составлению и решению системы линейно независимых уравнений, в которых в качестве неизвестных фигурируют токи и напряжения ветвей исследуемой цепи. Эти уравнения называются уравнениями электрического равновесия цепи. Общее число уравнений 2p: p уравнений по законам Кирхгофа, p компонентных уравнений.
Из компонентных уравнений можно исключить рит – уравнений, содержащих источники тока и рин – уравнений, содержащих только источники напряжения. Таким образом, 2р − рит − рин – уравнений и составляют основную систему уравнений электрического равновесия (ОСУ).
Уравнения электрического равновесия цепи представляют собой в общем случае систему алгебраических и интегро-дифференциальных уравнений.
Система уравнений может быть сведена к одному дифференциальному уравнению для любого из неизвестных токов или напряжений вида:
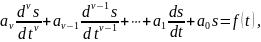
где
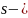 любой
неизвестный ток или напряжение;
любой
неизвестный ток или напряжение;
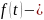 линейная
комбинация внешних воздействий в виде
источников энергии и их производных.
линейная
комбинация внешних воздействий в виде
источников энергии и их производных.
Такое уравнение называют дифференциальным уравнением цепи.
Порядок его определяет порядок цепи и задается числом независимых реактивных элементов.
Лекция 4 Линейные электрические цепи при гармоническом воздействии
Функция времени a(t,) изменяющаяся по синусоидальному или косинусоидальному закону вида
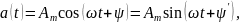 где
ψ'
= ψ
+ π/2,
то такая функция называется гармонической.
Будем использовать косинусоидальную
форму записи:
где
ψ'
= ψ
+ π/2,
то такая функция называется гармонической.
Будем использовать косинусоидальную
форму записи:
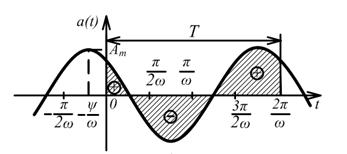
отрицательный полупериод
положительный полупериод
положительная полуволна
отрицательная полуволна
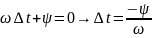
Амплитуда гармонической функции Am – это ее наибольшее значение; размерность [В] или [A].
Наименьшее значение: – Am.
Аргумент θ = ωt + ψ функции, записанной в косинусной форме, называется мгновенной фазой или просто фазой; измеряется в радианах или градусах.
Величина
ψ,
равная значению мгновенной фазы θ
при
t
= 0, называется начальной
фазой
гармонической
функции, измеряемой в радианах или
градусах:

Скорость ее изменения ω = dθ/dt называется угловой частотой. Она выражается в радианах в секунду (рад/с).
Гармоническая функция относится к периодическим функциям.
Функция времени называется периодической, если ее значения повторяются через определенные промежутки времени.
Наименьший промежуток времени T, через который наблюдается повторение значений функции, называется периодом.

где n — произвольное целое число.
Величина, обратная периоду T, называется частотой:
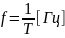
Функция cos θ является периодической функцией θ с периодом, равным 2π. Следовательно, изменение времени на период Т соответствует изменению фазы θ на 2π:
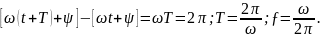
Определяют также положительный и отрицательный полупериоды.
Значения функции на положительном полупериоде – это положительные полуволны, на отрицательном – отрицательные полуволны.
С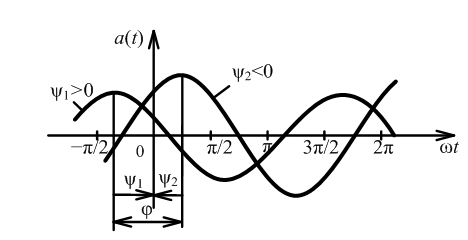 двиг
начальной фазы: аргумент t
двиг
начальной фазы: аргумент t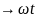 .
.
Вводят понятие разности фаз двух гармонических функций одной частоты:
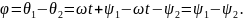
Если
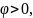 т.е.
т.е.
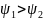 ,
то функция
,
то функция
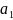 опережает функцию
опережает функцию
 .
.
Если
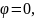 то функции совпадают по фазе.
то функции совпадают по фазе.
Если
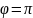 ,
то функции находятся в противофазе.
,
то функции находятся в противофазе.
Важнейшим свойством гармонических функций времени является то, что в результате линейных операций, производимых над ними (умножение на постоянное число, дифференцирование, интегрирование, алгебраическое сложение нескольких гармонических функций одинаковой частоты), получают гармонические функции той же частоты, но с изменением амплитуды и/или фазы.
Если а1(t) = Am1 cos(ωt + ψ1), то:
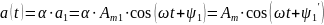 ;
;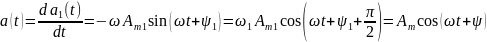
𝜓
;
𝜓
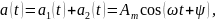 где
где
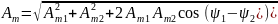 ;
;