Лекция 16 Первичные параметры составных четырехполюсников

Составным называется четырехполюсник, который может быть представлен как соединение нескольких более простых (элементарных) четырехполюсников.

Соединение четырехполюсников называется регулярным, если после их соединения токи зажимов 1 и 2 каждого четырехполюсника равны токам зажимов 1' и 2'.

Каскадное соединение:

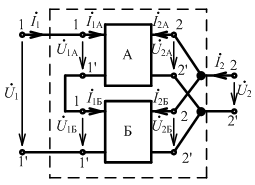
Каскадное соединение регулярное

При каскадном соединении:

;

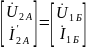
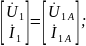
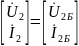Четырехполюсник А:

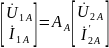
Четырехполюсник Б:

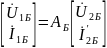
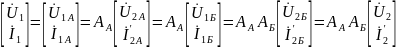
Матрица А – параметров составного четырехполюсника равна произведению матриц А – параметров элементарных четырехполюсников.

При каскадном соединении четырехполюсников:

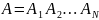
Так как произведение матриц не подчиняется переместительному закону, порядок расположения матриц должен соответствовать порядку следования четырехполюсников.

Параллельное соединение:

При параллельном соединении напряжения равны

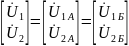, а токи составного четырехполюсника равны сумме токов элементарных четырехполюсников

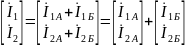
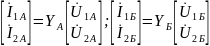
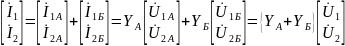
Y – параметры составного четырехполюсника равны сумме Y – параметров элементарных четырехполюсников.

Последовательное соединение:

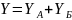
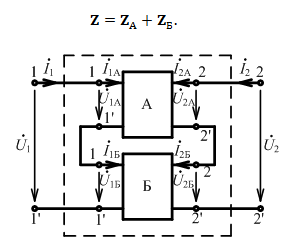
Параллельно – последовательное соединение:

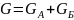
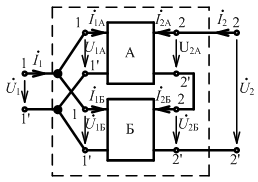
Последовательно – параллельное соединение:

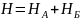
Использование данных правил возможно только при регулярных соединениях.

Соединение регулярно, если:

1. При параллельном соединении каждый четырехполюсник должен быть уравновешенным.

2. При параллельном и последовательном соединении четырехполюсников, имеющих общий вывод, все общие выводы соединяются.

3. Произвольный четырехполюсник соединяется с «разорванным» четырехполюсником:

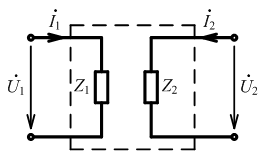
Схемы замещения неавтономных проходных четырехполюсников

Системе из 2 – х уравнений, содержащей 4 независимых коэффициента, можно поставить в соответствие идеализированную цепь, содержащую 4 элемента, параметры которых выражаются через независимые коэффициенты основной системы уравнений четырехполюсника.

Эквивалентные схемы могут быть разные. Широкое распространение получили T – образные и П – образные канонические схемы замещения:

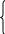
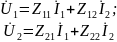
Можно найти:

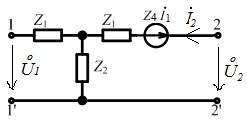
T – образный

П – образный

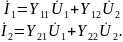
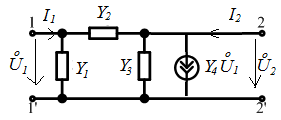
Можно найти:

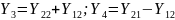
Для взаимных четырехполюсников

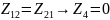
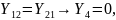т.е. нет управляемых источников.

Для симметричных четырехполюсников:

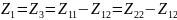
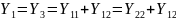
Схемы замещения с разделенными параметрами:

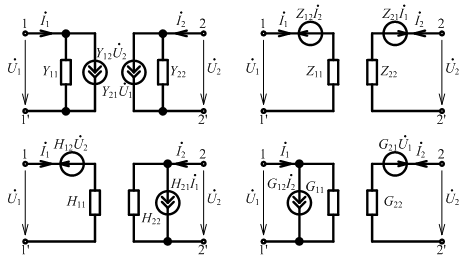
Автономные проходные четырехполюсники

П одключим к автономному четырехполюснику внешние источники ЭДС:

М

частичный ток

етодом контурных токов для контуров 1 и 2:

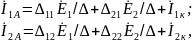
г

алгебраические дополнения

де

,

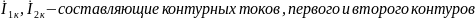вызванные действием независимых источников, находящихся внутри АЧ.

При одновременном закорачивании и :

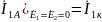
токи короткого замыкания

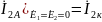
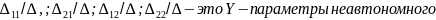
неавтономного четырехполюсника при выключении всех внутренних независимых источников.

Заменив 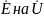, систему уравнений можно записать:

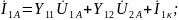
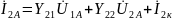
или , вводя :

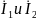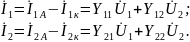
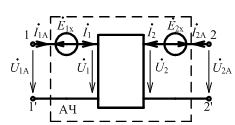
Э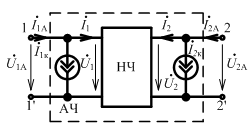 той системе уравнений соответствует эквивалентная схема вида:

НЧ – соответствующий неавтономный четырехполюсник

Каноническая П – образная схема автономного четырехполюсника:

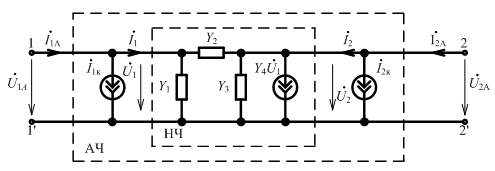
Методом узловых напряжений:

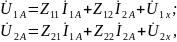
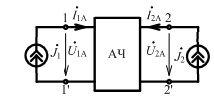
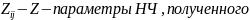
из АЧ путем выключения всех независимых источников.

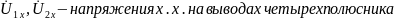
Э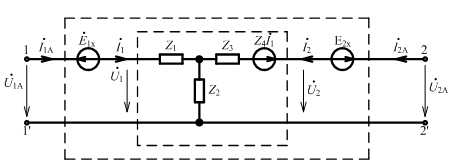 квивалентные схемы:

Канонический Т – образный