
- •Лекция 1
- •1.1. Основные определения Электрическая цепь
- •Электрический ток
- •Напряжение
- •Мощность и энергия
- •Схемы электрической цепи
- •Идеализированные пассивные элементы Резистивный элемент
- •Вольт-амперная характеристики резистора с линейным сопротивлением
- •Лекция 2 Емкостный элемент
- •Индуктивный элемент
- •Закон электромагнитной индукции:
- •Дуальные элементы цепи
- •Идеализированные активные элементы
- •Идеальный источник тока
- •Схемы замещения реальных источников
- •Управляемые источники тока и напряжения
- •Компонентные и топологические уравнения Законы Кирхгофа
- •Графы схем электрических цепей
- •Определение числа независимых узлов и контуров.
- •Основные задачи теории цепей
- •Понятие об уравнениях электрического равновесия
- •Лекция 4 Линейные электрические цепи при гармоническом воздействии
- •Понятие о среднем, средневыпрямленном и действующем значении гармонических токов и напряжений
- •Метод комплексных амплитуд
- •Комплексные изображения гармонических функций времени
- •Операции над комплексными изображениями гармонических функций
- •Лекция 5
- •Комплексная схема замещения цепи. Законы Ома и Кирхгофа в комплексной форме
- •Порядок анализа цепи методом комплексных амплитуд
- •Идеализированные пассивные элементы при гармоническом воздействии Резистивный элемент
- •Емкостный элемент
- •Индуктивный элемент
- •Лекция 6 Анализ простейших линейных цепей при гармоническом воздействии Последовательная rl-цепь
- •Последовательная rc – цепь
- •Последовательная rlc – цепь
- •Параллельная rlc – цепь
- •Делители напряжения и тока Делитель напряжения
- •Лекция 7 Энергетические процессы в простейших цепях при гармоническом воздействии Аналогии между механическими и электромагнитными процессами
- •Мгновенная мощность пассивного двухполюсника при гармоническом воздействии.
- •Активная, реактивная, полная и комплексная мощности
- •Баланс мощностей
- •Согласование источника энергии с нагрузкой
- •Лекция 8 Преобразования электрических цепей
- •Участки цепей с последовательным соединением элементов
- •Участки цепей с параллельным соединением элементов
- •Участки цепей со смешанным соединением элементов
- •Эквивалентное преобразование треугольника сопротивлений в звезду и обратное (самостоятельно)
- •Последовательная и параллельная схемы замещения пассивного двухполюсника
- •Перенос источников
- •Лекция 9 Цепи с взаимной индуктивностью
- •Понятие об одноименных зажимах
- •Коэффициент связи между индуктивными катушками
- •Цепи с взаимной индуктивностью при гармоническом воздействии
- •Эквивалентные преобразования участков цепей со связанными индуктивностями
- •Понятие о линейных трансформаторах
- •Лекция 10 Комплексные частотные характеристики линейных электрических цепей Понятие о комплексных частотных характеристиках
- •Комплексные частотные характеристики идеализированных двухполюсных пассивных элементов
- •Кчх цепей с одним реактивным элементом
- •Комплексный коэффициент передачи по напряжению
- •Логарифмические ачх и фчх
- •Лекция 11 Последовательный колебательный контур
- •Резонансная частота, характеристическое сопротивление и добротность контура
- •Энергетические процессы в последовательном колебательном контуре
- •Комплексные частотные характеристики
- •Передаточные характеристики контура
- •Лекция 12 Параллельный колебательный контур
- •Параллельный колебательный контур с разделенной индуктивностью
- •П араллельный колебательный контур с разделенной емкостью
- •Лекция 13 Методы формирования уравнений электрического равновесия цепи
- •Метод контурных токов (кт)
- •Метод узловых напряжений
- •Формирование уравнений электрического равновесия цепей с зависимыми источниками
- •Лекция 14 Основные теоремы теории цепей Принцип наложения (суперпозиции)
- •Теорема взаимности (обратимости)
- •Теорема компенсации
- •Теорема об эквивалентном источнике
- •Лекция 15 Многополюсники и цепи с многополюсными элементами
- •Классификация и схемы включения многополюсников
- •Основные уравнения и первичные параметры линейных неавтономных многополюсников
- •Основные уравнения и системы первичных параметров проходных четырехполюсников Классификация проходных четырехполюсников
- •Основные уравнения и основные параметры неавтономных проходных четырехполюсников
- •Методы определения первичных параметров четырехполюсников
- •Лекция 16 Первичные параметры составных четырехполюсников
- •Схемы замещения неавтономных проходных четырехполюсников
- •Автономные проходные четырехполюсники
- •Характеристические параметры и комплексные частотные характеристики (кчх) неавтономных проходных четырехполюсников к чх четырехполюсников при произвольной нагрузке
- •Характеристические сопротивления неавтономного проходного четырехполюсника
- •Характеристические постоянные передачи неавтономного проходного четырехполюсника
Формирование уравнений электрического равновесия цепей с зависимыми источниками
При наличии управляемых источников необходимо выразить управляющие токи или напряжения через независимые искомые переменные.
Составление уравнений выполняется в два этапа:
Управляемый источник тока или напряжения используется в ССУ как независимый;
его значения пересчитываются с учетом управляющих токов или напряжений, выраженных через искомые независимые переменные. После чего в ССУ в качестве неизвестных остаются только независимые переменные.
Пример:
м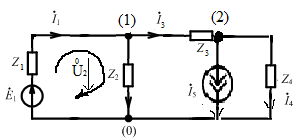 етод
ТВ:
етод
ТВ:
1

– й этап:
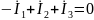



2
– й этап:

уравнение
2 УБТ:
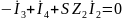
Выбор метода формирования ССУ
На практике наиболее применимым является метод УН, так как он, как правило, имеет меньшую размерность и не требует составления графа цепи и выбора главных контуров.
В методе УН формирование системы уравнений однозначно и просто формируется, а значит может быть использовано для автоматического составления ССУ.
Лекция 14 Основные теоремы теории цепей Принцип наложения (суперпозиции)
Р
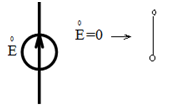
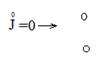 еакция
линейных электрических цепей на
произвольное внешнее воздействие,
представляющее собой линейную комбинацию
более простых воздействий, равна линейной
комбинации реакций, вызванных каждым
из простых воздействий в отдельности.
еакция
линейных электрических цепей на
произвольное внешнее воздействие,
представляющее собой линейную комбинацию
более простых воздействий, равна линейной
комбинации реакций, вызванных каждым
из простых воздействий в отдельности.
Для цепи, содержащей только источники напряжения, может быть составлена ССУ методом КТ (контурных токов).

ССУ может быть решена относительно контурных токов методом Крамера:

где
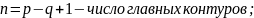


столбцом
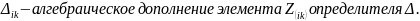


N — число независимых источников ЭДС;
Ykj
– передаточные проводимости, представляющие
собой алгебраические суммы слагаемых
вида
 ,
которые не зависят от ЭДС источников,
а определяются только параметрами
матрицы
,
которые не зависят от ЭДС источников,
а определяются только параметрами
матрицы
 .
.
Каждое
слагаемое
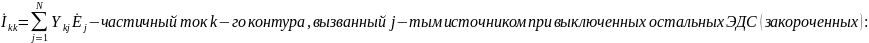
Следовательно, контурный ток равен сумме частичных токов, вызванных действием каждого источника напряжения в отдельности:
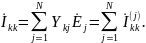
Остальные токи и напряжения цепи находятся из контурных токов.
Аналогично
при наличии источников тока, используя
метод УН, можно показать, что узловые
напряжения складываются из частичных
узловых напряжений
 ,
вызванных каждым источником тока в
отдельности
,
вызванных каждым источником тока в
отдельности
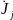 .
.
Частичные узловые напряжения определяются при выключенных (разорванных) остальных источниках тока:


передаточное сопротивление

В общем случае при наличии источников различного вида ток и напряжение любой k – той ветви могут быть найдены и выражений:

l – количество источников ЭДС, m – количество источников тока.
 =
(jω),
=
(jω),
 =
(jω)
— комплексные
коэффициенты передачи цепи по току и
напряжению;
=
(jω)
— комплексные
коэффициенты передачи цепи по току и
напряжению;
 =
(jω),
=
(jω),
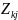 =
(jω)
— комплексные передаточные проводимости
и сопротивления.
=
(jω)
— комплексные передаточные проводимости
и сопротивления.
Элементы , , и находятся при выключенных источниках (E – к.з.; J – х.х.) кроме источника в j – той ветви.
Метод наложения, используемый при анализе цепи, основан на принципе наложения.
Теорема взаимности (обратимости)
Для линейной пассивной электрической цепи, состоящей из сопротивлений, емкостей и индуктивностей, в большинстве случаев связанных, справедлива теорема взаимности:
Для источника ЭДС контурный ток k-го контура цепи, вызванный действием источника напряжения, помещенного в i-й контур, равен контурному току i-гo контура, вызванного действием того же источника, перенесенного из i-го контура в k-й. Ориентация источника относительно контурного тока должна быть одинакова.
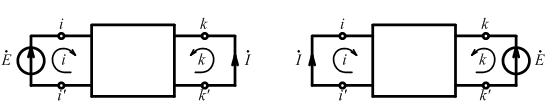
Используя метод КТ, можно показать:
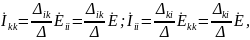
так
как
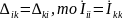 .
.
Для источника тока :
Если
источник тока
,
подключенный к паре зажимов, вызывает
на другой паре зажимов напряжение
,
то этот же источник тока, подключенный
ко второй паре зажимов, вызовет на первой
паре зажимов то же напряжение
 Ориентация источника тока относительно
напряжения на зажимах должна быть
одинакова.
Ориентация источника тока относительно
напряжения на зажимах должна быть
одинакова.
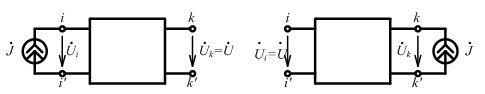
Цепь, удовлетворяющая теореме взаимности, называется взаимной или обратимой, не удовлетворяющая – невзаимной или необратимой.
