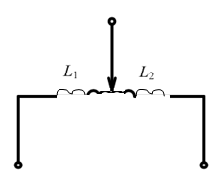
Параллельный колебательный контур с разделенной индуктивностью

Применим катушку индуктивностей, разделенную на части.

Катушка L₁ включается в первую ветвь, а катушка L₂ совместно с конденсатором – во вторую.

Коэффициент включения индуктивностей:

.

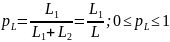П олучаем контур, R₁ = R_{L1 посл}

Вторая ветвь представляет собой последовательный колебательный контур, обладающий резонансом напряжений.

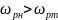
Входное сопротивление:

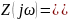
Для резонанса токов можно получить:

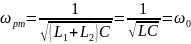
R₂ = R_{L2 посл} + R_{C посл}

Для резонанса напряжений:

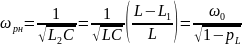
С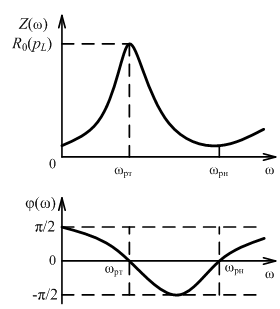 опротивление контура на резонансе токов:

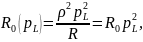R = R₁ + R₂, ρ = .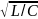

Сопротивление на резонансе напряжений:

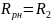
Добротность:

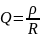
Токи ветвей:

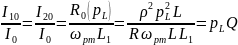
Таким образом, частота резонанса токов, характеристическое сопротивление и добротность не зависит от коэффициента включения .

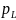Частота резонанса напряжений и резонансное сопротивление есть функции .

Разделение индуктивности часто используется для уменьшения влияния сопротивления нагрузки или источника энергии на добротность контура.

При подключении R_н к зажимам 1 — 1' .

Входное сопротивление контура на резонансе токов:

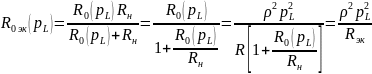
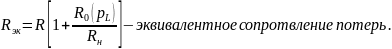
Эквивалентная добротность:

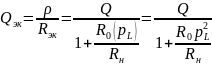
Изменяя можно уменьшить влияние на .

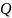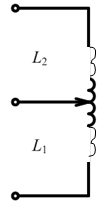
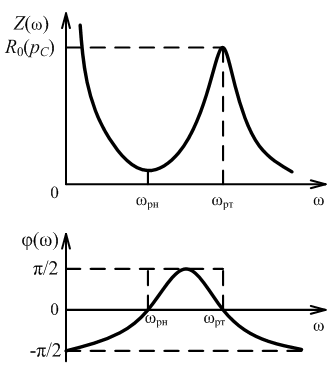
П араллельный колебательный контур с разделенной емкостью

Суммарная емкость С = С₁С₂/(С₁ + С₂).

Суммарное сопротивление R = R₁ + R₂

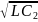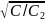ω_рн=1/  = ω₀   = ω₀

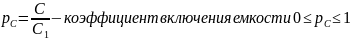
Резонансное сопротивление контура:

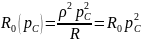
R₀ = ρ²/R.

Также используется для уменьшения влияния сопротивления нагрузки на добротность.

Лекция 13 Методы формирования уравнений электрического равновесия цепи

Е сли задана цепь, где p – число ветвей, q – число узлов, (р_ит – число ветвей, содержащих источник тока ,

р _ин – число ветвей, содержащих источник ) напряжения,

то основная система уравнений (ОСУ) электрического равновесия цепи содержит р топологических уравнений (q – 1-УБТ, p – q + 1-УБН) и р − р_ит − р_ин компонентных уравнений.

Таким образом, для сложных цепей получается ОСУ большой размерности.

Размерность системы уравнений можно уменьшить, если составить ее только для независимых переменных, тогда получается сокращенная система уравнений (ССУ).

Остальные переменные являются зависимыми и могут быть найдены через независимые с помощью компонентных или топологических уравнений.

Метод токов ветвей (ТВ)

Метод ТВ основан на том, что ток и напряжение каждой ветви, кроме вырожденных, связаны между собой компонентными уравнениями.

Рассмотрим на примерах:

Пример 1.

1. Цепь не содержит источника тока .

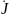1. Составим ОСУ:

q − 1 = 3 УБТ по I – му закону Кирхгофа

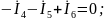
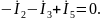
2. p − q + 1 = 3 УБН по II – му закону Кирхгофа

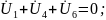
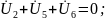
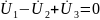
3. p - p_ин - p_ит = 6 компонентных уравнений

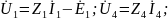
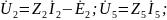
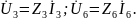
Всего 12 уравнений.

По методу ТВ необходимо УБН выразить напряжения через токи ветвей, используя компонентные уравнения:

УБТ УБН

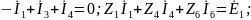
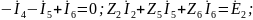
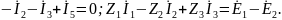
Всего 2p=6 уравнений в ССУ.

Пример 2. Цепь содержит источник тока :

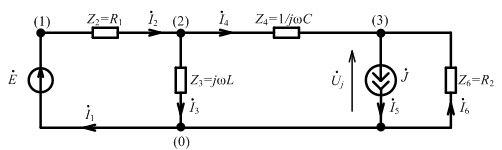
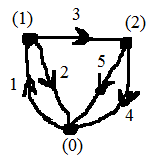
Выберем дерево так, чтобы источник тока был в главной ветви (не являлся ветвью дерева):

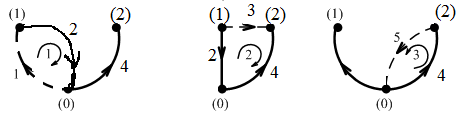
Неизвестных токов: р − р_ит=4

УБТ УБН

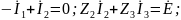
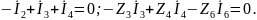
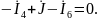
Для нахождения :

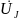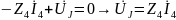
Таким образом, при использовании метода ТВ ССУ содержит q – 1 УБТ и p – q + 1 УБН, составленных для главных контуров, не содержащих ветвей с источником тока, причем напряжения ветвей выражены через соответствующие токи.

При решении такой системы находятся р − р_ит независимых токов ветвей.

Далее с помощью компонентных уравнений находятся напряжения невырожденных ветвей.

Напряжения вырожденных ветвей находятся из уравнений, составленных для контуров, содержащих вырожденные ветви.

Метод напряжений ветвей (НВ)

Является дуальным к методу ТВ.

Для примера компонентные уравнения:

; ; ; ; ; ;

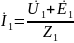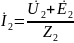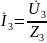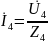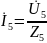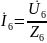УБТ:

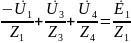1. ; (2) .

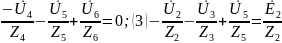В качестве независимых переменных используют неизвестные напряжения р − р_ин ветвей.

ССУ в этом случае содержит р − q + 1 УБН и q – 1 − р_ин уравнений баланса токов, составленных для главных сечений, не содержащих вырожденных ветвей.

Токи, входящие в УБТ, должны быть выражены через напряжения этих ветвей с использованием компонентных уравнений.