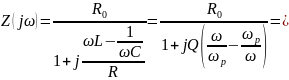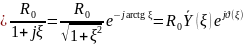- •Лекция 1
- •1.1. Основные определения Электрическая цепь
- •Электрический ток
- •Напряжение
- •Мощность и энергия
- •Схемы электрической цепи
- •Идеализированные пассивные элементы Резистивный элемент
- •Вольт-амперная характеристики резистора с линейным сопротивлением
- •Лекция 2 Емкостный элемент
- •Индуктивный элемент
- •Закон электромагнитной индукции:
- •Дуальные элементы цепи
- •Идеализированные активные элементы
- •Идеальный источник тока
- •Схемы замещения реальных источников
- •Управляемые источники тока и напряжения
- •Компонентные и топологические уравнения Законы Кирхгофа
- •Графы схем электрических цепей
- •Определение числа независимых узлов и контуров.
- •Основные задачи теории цепей
- •Понятие об уравнениях электрического равновесия
- •Лекция 4 Линейные электрические цепи при гармоническом воздействии
- •Понятие о среднем, средневыпрямленном и действующем значении гармонических токов и напряжений
- •Метод комплексных амплитуд
- •Комплексные изображения гармонических функций времени
- •Операции над комплексными изображениями гармонических функций
- •Лекция 5
- •Комплексная схема замещения цепи. Законы Ома и Кирхгофа в комплексной форме
- •Порядок анализа цепи методом комплексных амплитуд
- •Идеализированные пассивные элементы при гармоническом воздействии Резистивный элемент
- •Емкостный элемент
- •Индуктивный элемент
- •Лекция 6 Анализ простейших линейных цепей при гармоническом воздействии Последовательная rl-цепь
- •Последовательная rc – цепь
- •Последовательная rlc – цепь
- •Параллельная rlc – цепь
- •Делители напряжения и тока Делитель напряжения
- •Лекция 7 Энергетические процессы в простейших цепях при гармоническом воздействии Аналогии между механическими и электромагнитными процессами
- •Мгновенная мощность пассивного двухполюсника при гармоническом воздействии.
- •Активная, реактивная, полная и комплексная мощности
- •Баланс мощностей
- •Согласование источника энергии с нагрузкой
- •Лекция 8 Преобразования электрических цепей
- •Участки цепей с последовательным соединением элементов
- •Участки цепей с параллельным соединением элементов
- •Участки цепей со смешанным соединением элементов
- •Эквивалентное преобразование треугольника сопротивлений в звезду и обратное (самостоятельно)
- •Последовательная и параллельная схемы замещения пассивного двухполюсника
- •Перенос источников
- •Лекция 9 Цепи с взаимной индуктивностью
- •Понятие об одноименных зажимах
- •Коэффициент связи между индуктивными катушками
- •Цепи с взаимной индуктивностью при гармоническом воздействии
- •Эквивалентные преобразования участков цепей со связанными индуктивностями
- •Понятие о линейных трансформаторах
- •Лекция 10 Комплексные частотные характеристики линейных электрических цепей Понятие о комплексных частотных характеристиках
- •Комплексные частотные характеристики идеализированных двухполюсных пассивных элементов
- •Кчх цепей с одним реактивным элементом
- •Комплексный коэффициент передачи по напряжению
- •Логарифмические ачх и фчх
- •Лекция 11 Последовательный колебательный контур
- •Резонансная частота, характеристическое сопротивление и добротность контура
- •Энергетические процессы в последовательном колебательном контуре
- •Комплексные частотные характеристики
- •Передаточные характеристики контура
- •Лекция 12 Параллельный колебательный контур
- •Параллельный колебательный контур с разделенной индуктивностью
- •П араллельный колебательный контур с разделенной емкостью
- •Лекция 13 Методы формирования уравнений электрического равновесия цепи
- •Метод контурных токов (кт)
- •Метод узловых напряжений
- •Формирование уравнений электрического равновесия цепей с зависимыми источниками
- •Лекция 14 Основные теоремы теории цепей Принцип наложения (суперпозиции)
- •Теорема взаимности (обратимости)
- •Теорема компенсации
- •Теорема об эквивалентном источнике
- •Лекция 15 Многополюсники и цепи с многополюсными элементами
- •Классификация и схемы включения многополюсников
- •Основные уравнения и первичные параметры линейных неавтономных многополюсников
- •Основные уравнения и системы первичных параметров проходных четырехполюсников Классификация проходных четырехполюсников
- •Основные уравнения и основные параметры неавтономных проходных четырехполюсников
- •Методы определения первичных параметров четырехполюсников
- •Лекция 16 Первичные параметры составных четырехполюсников
- •Схемы замещения неавтономных проходных четырехполюсников
- •Автономные проходные четырехполюсники
- •Характеристические параметры и комплексные частотные характеристики (кчх) неавтономных проходных четырехполюсников к чх четырехполюсников при произвольной нагрузке
- •Характеристические сопротивления неавтономного проходного четырехполюсника
- •Характеристические постоянные передачи неавтономного проходного четырехполюсника
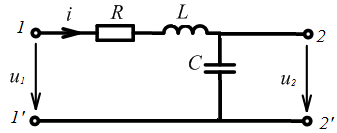
Передаточные характеристики контура
К
оэффициент
передачи контура по напряжению на
емкости
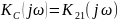 в режиме хх на зажимах 2
— 2' и 3 — 3'
в режиме хх на зажимах 2
— 2' и 3 — 3'
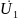
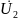
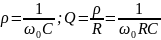 ;
;
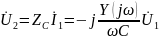
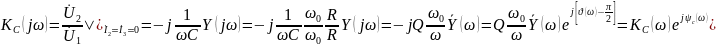
АЧХ коэффициента передачи по напряжению на емкости:
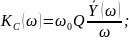
ФЧХ коэффициента передачи по напряжению на емкости:
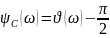
Аналогично находим комплексный коэффициент передачи по напряжению на индуктивности:
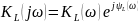
А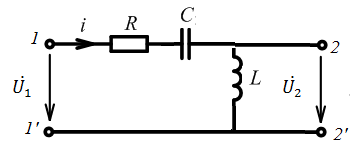 ЧХ:
ЧХ:
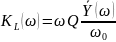
ФЧХ:
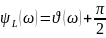
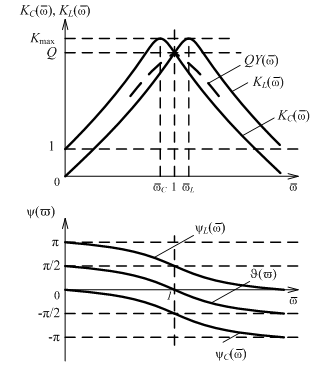
На резонансе:
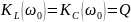
При
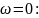
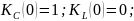
При
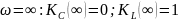
Максимальные
значения функции KС
max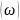 и
KL
max
принимают на частотах:
и
KL
max
принимают на частотах:
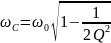
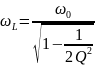
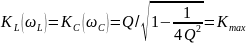
При
Q 5
5
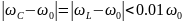
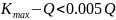
Поэтому:
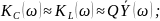
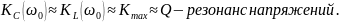
Избирательные свойства последовательного колебательного контура
Способность электрической цепи выделять колебания отдельных частот из суммы колебаний различных частот называется избирательностью.
В идеальном случае отклик избирательной цепи должен иметь постоянное значение в пределах определенного диапазона частот, называемого полосой пропускания цепи, и быть равным нулю за пределами этого диапазона.
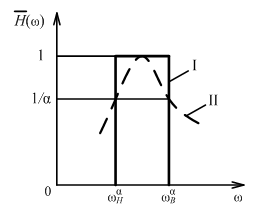
Нормированная АЧХ идеальной избирательной цепи имеет прямоугольную форму.
Реальные характеристики не имеют прямоугольной формы.
Полоса пропускания или ширина полосы пропускания реальных устройств на уровне 1/α:

или
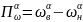 определяется
как диапазон частот, в котором амплитуда
отклика цепи не падает больше, чем в α
раз,
относительно своего максимального
значения.
определяется
как диапазон частот, в котором амплитуда
отклика цепи не падает больше, чем в α
раз,
относительно своего максимального
значения.
Чаще
всего полосу пропускания определяют
для
,
тогда
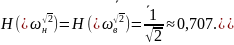
Избирательные свойства цепи иногда сравнивают с помощью коэффициента прямоугольности:
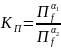 ,
где α2
<
α1;
у идеального избирательного устройства
,
где α2
<
α1;
у идеального избирательного устройства
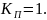
Часто α2 = , а α1=100.
Избирательные свойства последовательного колебательного контура определяются его нормированной АЧХ входной проводимости:
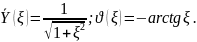
Полагая
ξ
=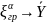 (
(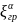 )
= 1/α
)
= 1/α
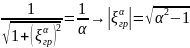 При
α
=
При
α
=
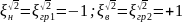
гр = ± π/4; |xгр.1,2| = |ωгр.1,2L − 1/( ωгр.1,2С)|=R.
Определим полосу пропускания последовательного колебательного контура:
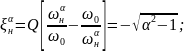
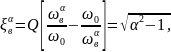
откуда:
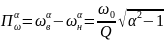
При α =
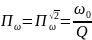 или
или
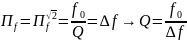 ;
;
прямоугольность
при α
=
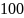
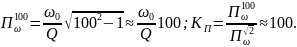
Следовательно, последовательный контур далек от идеального избирательного контура.
Влияние на добротность внутреннего сопротивления источника и сопротивления нагрузки
С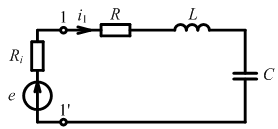 опротивление
источника последовательно включено с
сопротивлением потерь контура
опротивление
источника последовательно включено с
сопротивлением потерь контура
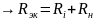 ;
добротность такого контура:
;
добротность такого контура:
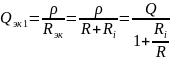 ;
Q = ρ/R.
;
Q = ρ/R.
Полоса
пропускания:
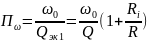 .
.
Для
улучшения эквивалентной добротности
контура необходимо
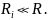
При подключенной нагрузке:
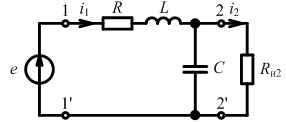
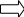
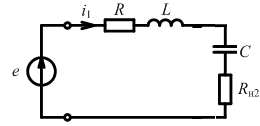
Переход к последовательной схеме замещения
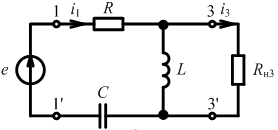
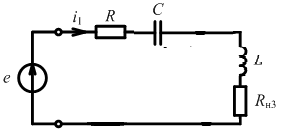
При высокой добротности:
С
внесенные в контур сопротивления нагрузки
посл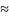 С;
С;
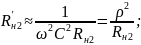
L
посл
L;
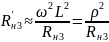
Чем больше сопротивление нагрузки, тем меньше внесенное.
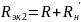
При одном сопротивлении нагрузки Rн эквивалентная добротность:
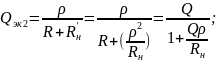
Полоса:
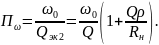
Для увеличения эквивалентной добротности:
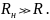
Лекция 12 Параллельный колебательный контур
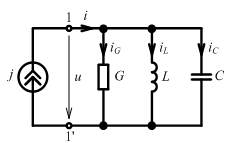
Параллельным колебательным контуром называется электрическая цепь, в которой индуктивные катушки и конденсаторы размещены в двух ветвях, подключенных параллельно источнику энергии.
Схема замещения:
Д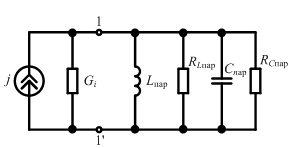 ля
элементов с высокой добротностью:
ля
элементов с высокой добротностью:
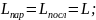
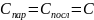
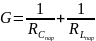
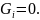
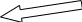
Было
установлено, что последовательная RLC
– цепь и параллельная RLC
– цепь дуальны (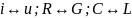 ),
поэтому все выражения могут быть получены
одни из других путем взаимной замены
токов и напряжений, сопротивлений и
проводимостей, емкостей и индуктивностей.
),
поэтому все выражения могут быть получены
одни из других путем взаимной замены
токов и напряжений, сопротивлений и
проводимостей, емкостей и индуктивностей.
На резонансной частоте мнимая составляющая входной проводимости должна быть равна «0»:
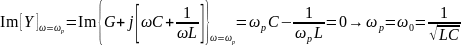 .
.
На
резонансной частоте полные проводимости
емкости
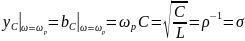
индуктивности
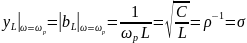
σ – характеристическая проводимость параллельного колебательного контура.
При
резонансе
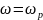 токи индуктивности и емкости имеют
одинаковые значения, но противоположны
по направлению. Действующие значения
токов реактивных элементов: IC
= IL = σU;
токи индуктивности и емкости имеют
одинаковые значения, но противоположны
по направлению. Действующие значения
токов реактивных элементов: IC
= IL = σU;
входной ток контура: I = IG = GU.
Добротность параллельного колебательного контура – это отношение тока реактивного элемента к входному току контура:
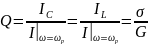 .
.
Влияние проводимости источника энергии и проводимости нагрузки на эквивалентную добротность параллельного контура:
G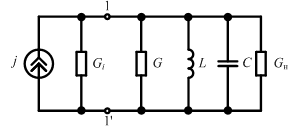
 эк.=G+
Gi+
Gн
эк.=G+
Gi+
Gн
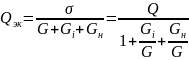 ;
;
поэтому для увеличения эквивалентной добротности контура необходимо, чтобы
Gi<<G и Gн<<G.
КЧХ параллельного колебательного контура:
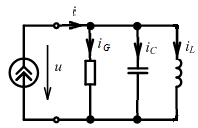
Входное
воздействие i
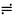
Отклики
u ≓
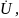 iC
iC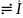 C,
iL
L .
C,
iL
L .
Входная КЧХ – комплексное входное сопротивление:

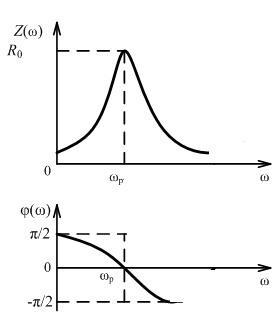
Нормированные характеристики:
А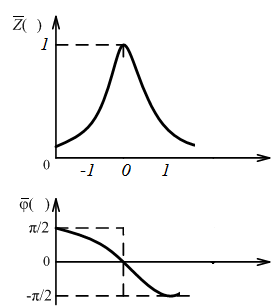
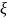
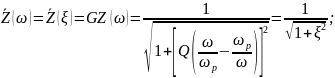
Ф
ЧХ
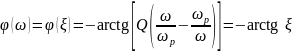
На резонансной частоте резонансное сопротивление контура:
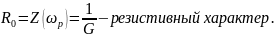
Коэффициент передачи по току:
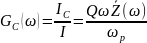
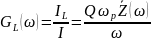
Q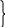
резонанс токов
>>1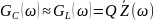
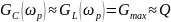
Несмотря на устройство получения выражений, на практике они используются редко, так как G сильно зависит от частоты:
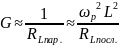
Чаще используется следующая схема замещения:
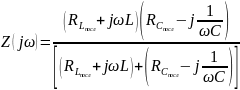
Э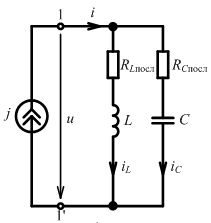 лементы
с высокой добротностью:
лементы
с высокой добротностью:
ρ
=
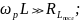 ρ
=
ρ
=
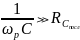
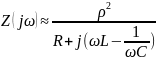 ;
ρ
=
;
ρ
=

Условие резонанса:
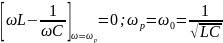
Резонансное сопротивление контура:
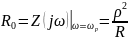
Ток
и напряжение на резонансной частоте
обозначим
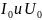 :
:
U0 = R0I0 = ρ2I0/R.
Токи емкости и индуктивности на резонансе:
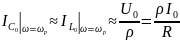
Добротность контура:
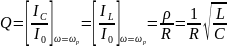
Таким образом, резонансная частота и добротность параллельного колебательного контура совпадает с резонансной частотой и добротностью последовательного колебательного контура, составленного из тех же элементов.
Входное сопротивление может быть представлено в виде: